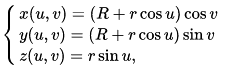toro
toro
toro superficie a forma di “ciambella”, generata dalla rotazione di una circonferenza di raggio r > 0 intorno a una retta a (suo asse di rotazione) complanare (cioè appartenente al suo piano) ed esterna a essa (il termine deriva dal latino torus, che significa «rialzo» e, per estensione, «guanciale, letto»). Nella rotazione spaziale, circonferenza e retta restano complanari, pur variando il piano all’interno di un fascio che ha tale retta come asse. Indicata con R > r la distanza del centro della circonferenza dall’asse a di rotazione e introdotto, nell’ordinario spazio euclideo, un riferimento Oxyz tale che l’asse z coincida con l’asse di rotazione e l’asse x passi per il centro della circonferenza, il toro è rappresentato da equazioni parametriche del tipo
(con u e ν tra 0 e 2π) e da equazione cartesiana (x 2 + y 2 + z 2 + R 2 − r 2)2 = 4R 2(x 2 + y 2). Spesso r è indicato come raggio minore e R come raggio maggiore del toro. Il toro è una superficie del quarto ordine, bicircolare, di genere geometrico 1 (→ genere). L’area della superficie del toro è 4π2 Rr e il volume da esso racchiuso è 2π2Rr 2.
Dal punto di vista topologico, il toro è equivalente all’insieme prodotto di due curve semplici chiuse, per esempio due circonferenze. Esso si può ottenere a partire da un rettangolo, identificando i lati opposti di un rettangolo, ossia “incollando” fra loro i lati opposti (→ identificazione). La nozione di toro si può generalizzare in diversi modi, per esempio considerando il prodotto topologico di due ipersuperfici sferiche oppure il prodotto di tre o più circonferenze oppure ciambelle con n buchi, dette anche n-tori.