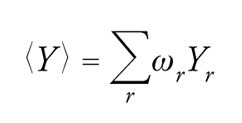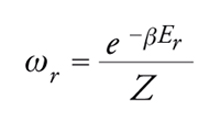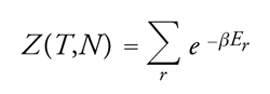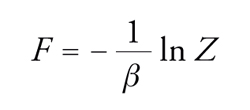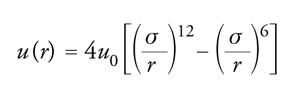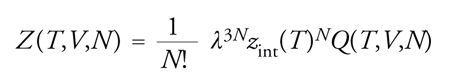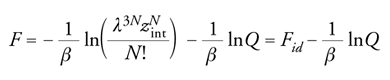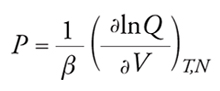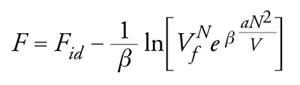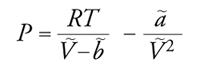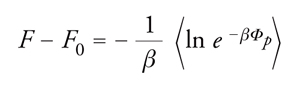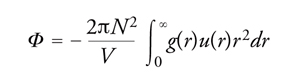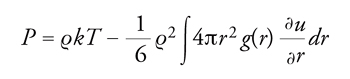Termodinamica molecolare

Termodinamica molecolare

La termodinamica classica macroscopica è stata definita come un insieme di utili relazioni fra diverse grandezze, ciascuna delle quali può essere misurata in modo indipendente. Questa definizione, anche se può apparire limitativa, mette in evidenza il ruolo essenziale della sperimentazione nell'intera disciplina. La termodinamica molecolare si differenzia da tale impostazione, in quanto si propone di studiare le caratteristiche degli stati di equilibrio della materia a partire dalla struttura delle molecole e dalla natura delle forze di interazione reciproca, mediante un vasto ricorso alla teoria e al calcolo. Essa, pertanto, costituisce una sintesi della termodinamica classica, della statistica e della chimica fisica molecolare, e ha raggiunto, attualmente, un'importanza tale da poter rivendicare una completa autonomia. La sua piena affermazione, inoltre, si è avvalsa ampiamente dello sviluppo del calcolo elettronico.

I diversi stati di aggregazione della materia possono essere rappresentati in uno spazio tridimensionale, che ha come coordinate la temperatura T, la pressione P e il volume specifico, riferito a una mole. Gli stati di equilibrio giacciono su una superficie che individua le zone di esistenza del gas, del liquido e del solido. Su tale superficie è riportata una serie di curve che indicano le trasformazioni a temperatura costante; una, in particolare, passa per il punto critico posto al confine fra le fasi liquida e gassosa e presenta un punto di flesso, la cui tangente si trova su un piano parallelo a quello P-V. Al di sotto della temperatura critica, le isoterme presentano un tratto orizzontale, i cui estremi delimitano i punti che caratterizzano gli stati liquido e gassoso tra loro in equilibrio. Il principale scopo della termodinamica molecolare è quello di individuare, fra le tre variabili menzionate, la relazione che, scritta in forma analitica, è chiamata equazione di stato.

Se nel sistema sono presenti più componenti, può avere luogo lo smiscelamento in più fasi condensate, liquide e solide, tra le quali si distribuiscono i componenti stessi. Il variegato comportamento della materia che ne deriva è profondamente condizionato dalle caratteristiche microscopiche dei componenti. Ciò giustifica l'approccio molecolare alla termodinamica, che, oltre a essere motivato da interessi scientifici, permette di risolvere problemi applicativi, riguardanti in particolare la progettazione degli impianti di liquefazione dei gas incoercibili, lo sviluppo dei processi di separazione dell'industria chimica e petrolifera, la caratterizzazione di materiali costituiti da miscele, lo studio della distribuzione di gas, gocce liquide e particelle solide presenti nell'atmosfera e della distribuzione degli idrocarburi nei giacimenti petroliferi.

Nelle industrie chimica e petrolifera, la separazione di miscele liquide contenenti diversi componenti è realizzata in colonne di distillazione (che possono raggiungere grandi dimensioni) in cui sono presenti diversi stadi, o 'piatti', sui quali fluiscono in controcorrente una fase vapore e una liquida, e dove i vari componenti si ripartiscono per cui i più volatili tendono ad accumularsi nella fase vapore.

La possibilità di poter descrivere, e al limite prevedere, le composizioni in equilibrio, costituisce un requisito importante nella progettazione di tali unità, che viene perseguito utilizzando appunto i risultati della termodinamica molecolare.

Presupposti statistici

In un sistema termodinamico a temperatura costante si possono individuare diverse configurazioni connesse con la distribuzione delle sue N molecole nello spazio, a ciascuna delle quali corrisponde un valore E_r dell'energia e uno Y_r di una generica grandezza osservabile, il cui valore medio all'equilibrio si ottiene mediante la relazione:

[1] formula.

La probabilità ω_r che il sistema si trovi nella configurazione r è espressa mediante la seguente legge di distribuzione canonica:

[2] formula

dove β=1/kT, essendo k la costante di Boltzmann. La quantità:

[3] formula

infine, è nota come funzione di ripartizione del sistema. La [2] è stata definita da Richard Feynman "la vetta della meccanica statistica, disciplina che nel suo complesso discende da essa, in quanto applicazione di un principio a casi particolari, oppure a essa risale, qualora si illustri la derivazione di tale legge fondamentale e si chiarisca il significato dei concetti di equilibrio termico e temperatura".

Nota la funzione di ripartizione, si possono valutare le principali grandezze termodinamiche, prima fra tutte la funzione energia libera di Helmholtz F mediante la relazione seguente:

[4] formula.

tab. 1

Le variazioni di energia libera forniscono il lavoro utile associato a una trasformazione reversibile e, per questo motivo, tale funzione riveste un ruolo di primaria importanza in termodinamica; grazie a essa si possono valutare, inoltre, l'energia interna, l'entropia, la pressione del sistema e il potenziale chimico di ciascuno dei componenti, attraverso le formule riassunte nella tab. 1. Di particolare attenzione per la trattazione in corso sono la formula [III], dalla quale si ricava una relazione fra temperatura, pressione, volume e composizione, vale a dire l'equazione di stato, e la formula [IV], che permette di ottenere il potenziale chimico, ossia la grandezza intensiva impiegata per caratterizzare lo stato di equilibrio in un sistema a più fasi e a più componenti.

fig. 2

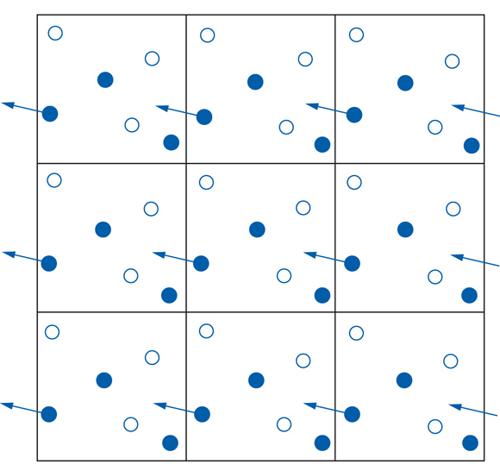
Un'applicazione diretta della [1] si riscontra nelle tecniche di simulazione, che negli ultimi anni hanno trovato ampia diffusione grazie allo sviluppo del calcolo elettronico. Nel metodo Monte Carlo, per esempio, si considerano alcuni sistemi modello, costituiti da centinaia, se non migliaia, di oggetti che rappresentano le molecole contenute in un volume V, e si effettua la media delle proprietà che competono a diverse loro configurazioni, costruite a caso mediante la generazione ‒ attraverso moti casuali delle singole molecole ‒ di una catena stocastica di eventi, detta markoviana. Un esempio, riferito per semplicità a un sistema bidimensionale di sei particelle, è illustrato nella fig. 2. Questi metodi di simulazione hanno raggiunto ormai un notevole livello di sofisticazione sia per la loro capacità di descrivere sistemi di ampie dimensioni, sia ‒ soprattutto ‒ per l'uso di modelli molecolari sempre più complessi e realistici. I risultati ottenuti si sono rivelati di grande importanza concettuale, ma è necessario lavorare ancora alla ricerca di espressioni analitiche, che risultino di rapida e agevole applicazione.

Forze intermolecolari

fig. 3

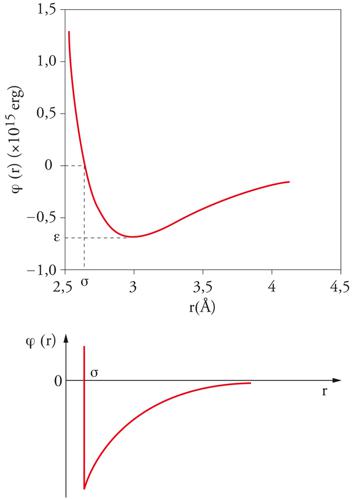
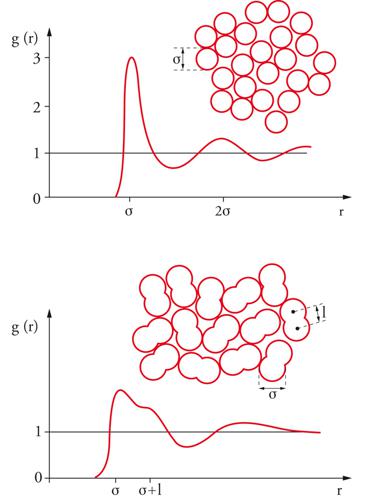
In un fluido semplice, le molecole interagiscono mediante un potenziale intermolecolare di tipo centrale, che dipende unicamente dalla distanza fra i centri di massa delle molecole. In senso stretto, appartengono a questa categoria solamente i sistemi costituiti da gas monoatomici, sebbene si possano considerare 'semplici' anche quei fluidi, quali l'ossigeno, l'azoto e il metano, le cui molecole sono relativamente piccole e compatte. In questo caso il potenziale intermolecolare u(r) è descritto da una curva che ha l'andamento illustrato nella fig. 3. A piccole distanze si manifestano forze repulsive, il cui potenziale cresce rapidamente al diminuire di r; all'aumentare della distanza, invece, prevalgono le forze attrattive. Al tendere della distanza all'infinito, il potenziale si annulla, in quanto l'interazione fra le molecole viene meno. La repulsione che agisce a piccole distanze è dovuta alla sovrapposizione delle nuvole elettroniche delle molecole, mentre l'attrazione, secondo l'interpretazione formulata da Fritz London, nasce dall'interazione istantanea fra le molecole, dovuta ai dipoli creati dai moti dei loro elettroni, che tendono a oscillare in modo sincrono o simpatetico. Nella figura si possono identificare due parametri caratteristici, σ e u₀, che rappresentano rispettivamente la distanza alla quale il potenziale si annulla e il valore minimo che esso assume. L'espressione analitica del potenziale menzionato si può compendiare nella seguente espressione, nota come potenziale di Lennard-Jones:

[5] formula.

L'interazione attrattiva, detta di dispersione, è inversamente proporzionale alla sesta potenza della distanza fra i centri di massa delle due molecole, in accordo con la teoria di London, e i parametri possono essere determinati da informazioni di natura sperimentale relative al comportamento dei fluidi. Nelle molecole dotate di un momento elettrico dipolare permanente si manifesta, ovviamente, anche un'interazione elettrostatica fra i dipoli, che dipende dall'orientazione tra le molecole stesse. In questi casi i potenziali hanno caratteristiche anisotrope, poiché dipendono, oltre che dalla distanza r, anche dagli angoli che descrivono l'orientazione reciproca delle molecole interagenti. Tenendo conto di ciò, il potenziale relativo a una coppia di molecole si può esprimere come somma di diversi termini che, oltre alle già citate interazioni dispersive, descrivono, rispettivamente, le interazioni elettrostatiche dovute ai dipoli permanenti e quelle induttive, originate dalle distorsioni delle nubi elettroniche per effetto delle molecole vicine. Anche se la chimica teorica e computazionale ha conseguito in questi ultimi anni diversi importanti successi nel calcolo delle energie molecolari, la valutazione a priori ‒ ossia a partire dai principî della meccanica quantistica ‒ delle forze intermolecolari presenta ancora incertezze. Nello studio degli equilibri tra fasi, perciò, si fa ampio uso di potenziali efficaci, che si riconducono essenzialmente a quello di Lennard-Jones e dipendono da parametri valutati per via semiempirica.

Una questione importante riguarda la 'trasferibilità' delle interazioni fra singoli atomi, o gruppi atomici, presenti nelle molecole. Si tratta di un aspetto direttamente connesso con i modelli cosiddetti dei contributi di gruppo, che hanno acquistato una particolare rilevanza in diverse applicazioni pratiche. In base a questa schematizzazione, il potenziale relativo a due molecole è espresso dalla somma delle interazioni corrispondenti ai diversi gruppi di atomi nei quali la molecola può essere decomposta. Ricordiamo, infine, che un atomo di idrogeno può agire all'interno di una molecola come elemento legante fra un atomo elettronegativo, al quale è unito con un legame covalente, e un altro atomo elettronegativo, quale il fluoro, l'ossigeno o l'azoto. A questo legame, chiamato 'a idrogeno', corrisponde un'energia minore di quella dei legami covalenti. Gli ordini di grandezza delle energie che entrano in gioco nelle interazioni molecolari sono infatti i seguenti:

(a) forze di non legame 0,2÷2 kcal/mol;

(b) legame a idrogeno 2÷10 kcal/mol;

(c) legami covalenti 50÷100 kcal/mol.

fig. 4

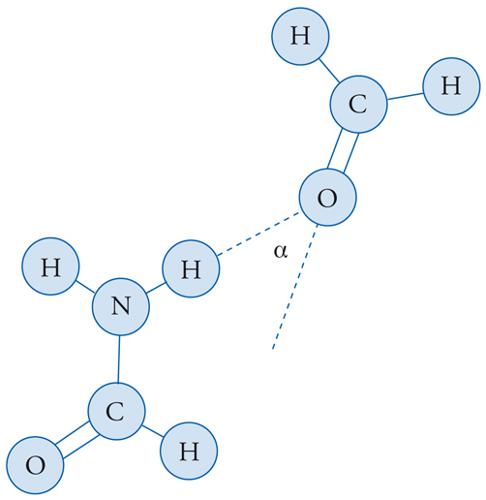
Esempi significativi di legami a idrogeno si trovano nell'acido fluoridrico e nell'acqua. Se essi sono presenti, le forze elettrostatiche assumono ovviamente un ruolo dominante, come è illustrato nella fig. 4, relativa all'interazione fra una molecola di formammide e una di formaldeide. In effetti, molte molecole della chimica organica hanno una struttura relativamente complessa, allungata, ramificata oppure ciclica, e in questi casi è opportuno scomporre l'interazione nei diversi contributi dei gruppi di atomi in esse presenti.

tab. 2

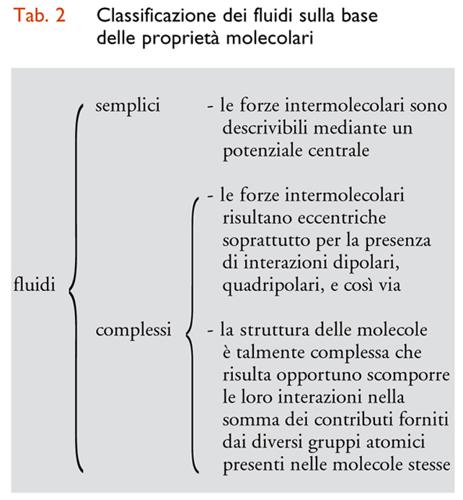
In conclusione, per l'analisi che segue è conveniente suddividere i fluidi in semplici e complessi, in relazione alle caratteristiche delle molecole di cui sono costituiti e sulla base della classificazione riportata nella tab. 2.

Funzione energia libera

fig. 5

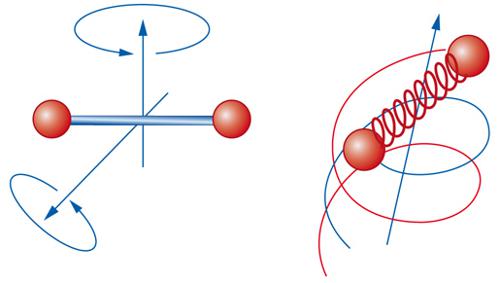
Il modello del gas perfetto costituisce il 'cavallo di battaglia' per chi deve affrontare la descrizione del comportamento di sistemi gassosi a pressioni relativamente basse e a temperature relativamente alte. La sua semplice equazione di stato, infatti, è stata formulata estrapolando il comportamento dei gas quando la pressione tende a zero. Dal punto di vista microscopico, le caratteristiche del gas perfetto sono ambigue, poiché le molecole sono assimilate a punti privi di interazioni, pur avendo una struttura i cui moti interni, illustrati nella fig. 5, contribuiscono a determinare l'energia del gas stesso. In ogni caso, il modello del gas perfetto, pur non permettendo di descrivere il comportamento dei gas in prossimità dei punti di condensazione, costituisce un valido riferimento per la descrizione della materia nei suoi diversi stati. Ciò premesso, per un fluido di un solo componente, contenente N molecole di massa m in un volume V, la funzione di ripartizione Z si può esprimere in generale come segue:

[6] formula.

Il termine λ=h/(2πmkT )^1/2, dove h è la costante di Planck, si chiama lunghezza d'onda di de Broglie e dipende dal moto traslazionale della molecola. La funzione di ripartizione molecolare z_int(T), relativa ai moti interni della molecola stessa, riflette il contributo dovuto a vibrazioni e rotazioni. La sua forma specifica è legata alle caratteristiche geometriche e dinamiche della molecola, ma, in generale, non al volume: nell'analisi che segue non sarà considerata esplicitamente, poiché non contribuisce a determinare il comportamento di stato del sistema in esame. Q è chiamato integrale delle configurazioni ed è definito dalla seguente relazione:

[7] Q(T,V,N)= Q=∫...∫e^{−βΦ(r1,r2,...,rN)}dr₁dr₂...dr_N ,

dove dr_1,, dr₂,←, dr_N sono gli elementi di volume centrati sulle posizioni delle molecole individuate dai vettori r₁, r₂,←, r_N, mentre Φ è l'energia potenziale totale, dovuta alle interazioni fra le molecole. Per un gas perfetto Φ è nullo.

Introducendo la [6] nella [3], si ottiene:

[8] formula

dove F_id dipende dalla sola temperatura. Se, tenendo conto di ciò, si utilizza l'equazione [III] della tab. 1, si ottiene:

[9] formula

che fornisce l'equazione di stato del sistema. Perché essa risulti valida anche in prossimità del punto critico, dove la funzione energia libera presenta un comportamento non analitico, è opportuno riferirsi al valore di Q per una singola molecola e far tendere sia N sia V all'infinito, mantenendo però fisso il valore della densità molecolare ϱ=N/V, secondo un procedimento chiamato del limite termodinamico. In realtà, l'applicabilità dell'equazione [9] è fortemente limitata dal fatto che l'integrale delle configurazioni Q è calcolabile soltanto se sono introdotte opportune approssimazioni, la più drastica delle quali è, ovviamente, di assumere che Φ sia nullo, nel qual caso Q risulta uguale a V ^N e l'equazione di stato del gas perfetto PV=NkT è di immediata deduzione.

L'energia potenziale Φ dell'insieme delle molecole può essere valutata sommando i potenziali intermolecolari delle diverse coppie di molecole. In prima approssimazione, si può assumere che queste ultime abbiano una distribuzione uniforme nello spazio e che ciascuna sia soggetta a un campo di energia potenziale medio, non influenzato dalle fluttuazioni dovute ai moti molecolari. Si può inoltre ipotizzare che le interazioni siano descrivibili mediante un potenziale 'a nocciolo duro', come quello illustrato nella fig. 3 in basso, assumendo inoltre che la regione attrattiva abbia l'andamento −u₀(σ/r)⁶, compatibile con il potenziale di Lennard-Jones [5]. Poiché il numero di coppie di molecole presenti nel sistema è dato da (1/2)N(N −1) ∼ N², l'energia potenziale media sarà Φ=−aN²/V, essendo a un coefficiente numerico, che risulta uguale a (2π/3)σ³u₀. Il segno meno per Φ è dovuto al fatto che, sulla base del potenziale adottato, l'energia è sempre negativa. Il valore medio dell'integrale [7] si può scrivere pertanto 〈Q 〉∼exp(βaN²/V). Le molecole, inoltre, non possono avvicinarsi al di sotto di una distanza uguale a σ ed è opportuno definire perciò un covolume b=(2π/3)Nσ³, che rappresenta il volume non accessibile alle molecole a causa dell'impenetrabilità della regione 'dura' del potenziale.

Tenendo conto di ciò, l'espressione dell'energia libera assume la forma:

[10] formula,

dove V_f=V−b è il cosiddetto volume libero, o accessibile alle molecole, mentre il parametro a è connesso alla regione attrattiva del potenziale. Se si sostituisce la precedente nella [9] si ricava la nota equazione di stato di van der Waals:

[11] formula,

fig. 6

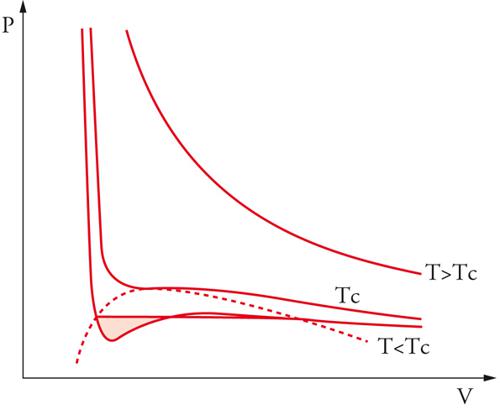
le cui isoterme hanno i tipici andamenti riportati nella fig. 6. Nell'equazione precedente, V∼, ã e b∼ si riferiscono a una mole di fluido e N è il numero di Avogadro, che, moltiplicato per k, fornisce la costante dei gas R. A temperatura elevata, l'andamento delle isoterme si avvicina a quello di iperboli equilatere, tipiche del gas perfetto, mentre, in corrispondenza della temperatura critica T_C, l'isoterma presenta un flesso orizzontale; in figura è riportato anche l'andamento delle curve isoterme per temperature inferiori. La presenza di un tratto nel quale la pressione aumenta all'aumentare del volume corrisponde a uno stato di equilibrio instabile, in cui un piccolo cambiamento delle variabili che lo caratterizzano è sufficiente a indurre una brusca trasformazione spontanea verso un sistema bifasico, costituito da una miscela di liquido e vapore in equilibrio. L'individuazione delle caratteristiche dei due stati in equilibrio può essere condotta mediante la costruzione grafica proposta da James C. Maxwell, in base alla quale le due aree bianche indicate in figura devono essere uguali: nei punti A e B l'energia libera molare dovrà assumere uguale valore, per cui, se si valuta la sua variazione lungo l'isoterma espressa dall'integrale di VdP, essa si annulla solamente se le due aree bianche risultano uguali. Ne deriva, quindi, un criterio per tracciare il segmento orizzontale che congiunge i due stati in equilibrio. Applicando il procedimento a diverse isoterme si individua così una successione di punti che, uniti fra loro, definiscono la tipica curva a campana, detta di Andrews, che individua le zone di coesistenza tra le due fasi. Mediante l'equazione [11], pertanto, è possibile dare una descrizione completa del comportamento di stato di un fluido, compresi gli stati di vapore e quello liquido.

Metodi perturbativi

Le tecniche perturbative trovano applicazione in diversi campi della fisica, per esempio in meccanica quantistica e in astronomia, in cui, preso come riferimento un opportuno sistema meccanico imperturbato, alcune proprietà di un sistema perturbato sono espresse sulla base di quelle già note. In termodinamica possono essere utilmente impiegate per il calcolo della funzione energia libera. A tale scopo, è opportuno esprimere l'energia potenziale del sistema come somma di due contributi:

[12] Φ = Φ₀ + Φ_p .

Il primo di essi corrisponde a un sistema scelto come riferimento e il secondo è un termine correttivo, che può essere considerato come una perturbazione del precedente. Se si indica con F₀ l'energia libera del sistema iniziale, si può scrivere:

[13] formula.

Tale quantità rappresenta il valore medio dell'esponenziale exp(−βΦ_p) dell'energia perturbativa, valutata ricorrendo alla funzione di distribuzione canonica [2] del sistema preso come riferimento.

La scelta più immediata cade su un sistema costituito da sfere dure non interagenti, le cui caratteristiche sono ben note grazie a studi di simulazione dettagliati, condotti sia con il metodo Monte Carlo sia mediante la dinamica molecolare. È possibile estendere la tecnica a vari sistemi, costituiti da oggetti aventi strutture geometriche varie, quali dischi, ellissoidi, sigari, e così via, simulando in modo sempre più adeguato la forma del nocciolo duro delle molecole. I risultati così ottenuti sono soddisfacenti per la descrizione del comportamento termodinamico di diversi fluidi. L'applicazione di tale metodo alle miscele dipende dal grado di conoscenza delle forze che agiscono tra molecole diverse. Solitamente, sono introdotte regole opportune, dette di mescolamento, in virtù delle quali è possibile risalire, a partire dai parametri del potenziale di molecole singole, a quelli di molecole differenti. Un criterio che trova frequente applicazione è quello di valutare σ e u₀ sulla base, rispettivamente, della media aritmetica e della media geometrica dei valori che si riferiscono ai singoli componenti. In realtà, per ottenere una soddisfacente descrizione dei dati sperimentali relativi a miscele, risulta necessario moltiplicare il valore medio di u₀ per un opportuno parametro empirico.

fig. 7 in alto e in basso

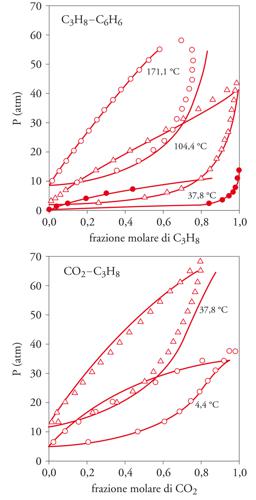
Questo approccio ha permesso di descrivere con accuratezza, e in funzione dei soli parametri del potenziale intermolecolare, l'equilibrio liquido-vapore di miscele di diversi componenti ‒ in particolare di idrocarburi, come illustrato nelle fig. 7 in alto e in basso. Tali indagini hanno messo in rilievo l'importanza che riveste il potenziale intermolecolare, al cui andamento sono molto sensibili i risultati dei calcoli di simulazione, e ciò evidenzia il ruolo delle ricerche di carattere teorico intese ad approfondire le caratteristiche e la forma dei potenziali intermolecolari. L'applicazione può essere estesa a fluidi costituiti da molecole polari, per le quali si prende a riferimento un fluido di molecole del tipo Lennard-Jones e si considera, quale termine perturbativo, l'attrazione fra i dipoli.

fig. 8

Le proprietà termodinamiche di un fluido possono essere valutate anche ricorrendo a un'opportuna funzione g(r), detta di distribuzione radiale, che descrive le variazioni locali di densità medie, che si manifestano nell'intorno di una molecola. A partire dal centro di una molecola, sono presenti, come illustrato nella fig. 8, variazioni di densità che riflettono la struttura locale del sistema. Si può osservare che all'aumentare di r la funzione di distribuzione radiale si avvicina al valore 1, poiché, per elevate distanze dalla molecola di riferimento, l'interazione con le molecole circostanti tende a uniformarsi e il valore medio della densità raggiunge quella del fluido stesso. La funzione di distribuzione radiale può essere determinata sperimentalmente, inviando sul campione un fascio collimato monocromatico di raggi X o di neutroni e misurando l'intensità della radiazione diffratta. Dalla funzione di distribuzione radiale si calcola l'energia potenziale del fluido come segue:

[14] formula.

La pressione del sistema, inoltre, può essere espressa nella forma:

[15] formula

da cui si può risalire all'equazione di stato senza coinvolgere l'energia libera. Le precedenti relazioni si possono applicare anche nell'ambito della teoria delle perturbazioni, se si impiega la funzione di distribuzione radiale del sistema preso come riferimento.

Applicazione alle molecole complesse

La teoria formulata nel 1873 da Johannes Diderik van der Waals ha costituito un approccio pionieristico allo studio delle proprietà della materia, poiché ha permesso di formulare una semplice equazione di stato che, opportunamente interpretata, di un fluido permette di descrivere entrambe le fasi ‒ liquida e vapore ‒ in equilibrio. I suoi limiti sono dovuti alle caratteristiche del potenziale intermolecolare impiegato e all'ipotesi che le molecole si distribuiscano omogeneamente nello spazio. Ci si è chiesti se, utilizzando espressioni più accurate per il calcolo del volume libero accessibile alle molecole, non fosse possibile apportare miglioramenti a tale equazione. Approfondendo lo studio sul comportamento dei sistemi formati da sfere dure, si è ottenuta la seguente espressione per il volume libero:

[16] V_f = Ve ^{η(3η−4)/(1−η)2}

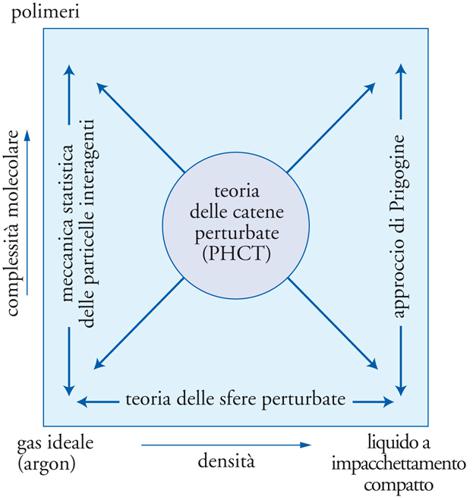
dove la quantità η=(1/6)πϱσ³ è sensibilmente diversa dalla differenza V−b=V(1−4η) presente nella versione originale della teoria. Nell'ambito dei modelli sinora considerati, le molecole sono state assimilate a oggetti interagenti dotati di forme e dimensioni particolari, ma privi di una struttura interna, poiché i loro movimenti di rotazione e di vibrazione non sono influenzati dall'ambiente che li circonda e pertanto non influiscono sull'equazione di stato. Questa ipotesi, rigorosamente valida per i gas monoatomici, costituisce una ragionevole approssimazione per piccole molecole poliatomiche, ma risulta inadeguata per molecole di grandi dimensioni, quali gli idrocarburi con più di 10 atomi di carbonio e, a maggior ragione, per i polimeri.

fig. 9

Una molecola costituita da n atomi possiede 3n gradi di libertà, di cui 3 sono associati al suo moto traslazionale, 3 al moto di rotazione attorno ad altrettanti assi ortogonali, aventi per origine il suo centro di massa, e i rimanenti ai diversi moti di vibrazione. È opportuno tenere presente che, secondo una proposta avanzata originariamente da Ilya Prigogine, le rotazioni e le vibrazioni di una molecola allungata possono risultare influenzate, in virtù della sua flessibilità e a causa di interazioni steriche, dalla presenza di molecole vicine. L'effetto ovviamente sparisce quando la densità del fluido tende a zero e le molecole risultano talmente diluite da riprodurre il comportamento del gas perfetto. Se, viceversa, il volume del sistema si riduce a quello dell'addensamento massimo di molecole, tutti i gradi di libertà associati ai loro movimenti esterni sono bloccati. L'impostazione precedente ha permesso di sviluppare modelli più generali, fra i quali merita di essere menzionato quello denominato PHCT (Perturbed hard-chain theory), che fornisce un'equazione di stato il cui campo di applicazione si estende dai fluidi costituiti da molecole semplici a quelli formati da molecole complesse, in un intervallo di densità che va dai gas perfetti ai liquidi con massimo addensamento (fig. 9). Esistono diverse varianti di questo modello, che dipendono sia dalle espressioni impiegate per il volume libero sia dal metodo utilizzato per valutare l'interazione attrattiva fra le molecole.

La termodinamica molecolare riveste un ruolo di primo piano nello studio dell'equilibrio dei fluidi. È stato dato particolare rilievo all'impiego delle equazioni di stato, per la descrizione non solamente di componenti puri, ma anche di miscele, seguendo l'approccio più moderno ed efficace. Nell'ambito di questa impostazione, acquistano grande risalto le ricerche sulle forze intermolecolari, soprattutto quelle tra molecole che differiscono l'una dall'altra. Un ulteriore problema di rilievo riguarda le interfasi fluido-solido e coinvolge i processi di adsorbimento, con particolare attenzione ai materiali con struttura porosa regolare, quali le zeoliti. Un argomento che è stato soltanto sfiorato, ma che merita attenta considerazione, riguarda infine le regioni critiche e supercritiche. In prossimità delle temperature critiche degli equilibri tra una fase liquida e una vapore, e fra due fasi liquide, si manifestano infatti comportamenti regolati da opportune leggi di scala. Si tratta, all'interno dello spazio che individua l'equilibrio tra fasi, di regioni che rivestono uno speciale interesse, non solamente scientifico, ma anche applicativo, poiché le zone supercritiche sono coinvolte in particolari processi di separazione.

Bibliografia

Barker, Henderson 1976: Barker, John A. - Henderson Douglas, What is "liquid"? Understanding the states of matter, "Reviews of modern physics", 48, 1976, pp. 587-671.

Carrà 1990: Carrà, Sergio, Termodinamica, Torino, Bollati Boringhieri, 1990.

Carrà 1998: Carrà, Sergio, Termodinamica molecolare, in: Enciclopedia del Novecento, Suppl. II, Roma, Istituto della Enciclopedia Italiana, 1998, pp. 786-800.

Chandler 1987: Chandler, David, Introduction to modern statistical mechanics, New York-Oxford, Oxford University Press, 1987.

Feynman 1972: Feynman, Richard P., Statistical mechanics, Reading (Mass.), Benjamin, 1972.

Gubbins 1994: Gubbins, Keith E., Application of molecular theory to phase equilibrium prediction, in: Model for thermodynamics and phase equilibria calculations, edited by Stanley I. Sandler, New York, Dekker, 1994.

McGlashan 1966: McGlashan, Maxwell L., The use and misuse of the laws of thermodynamics, "Journal of chemical education", 43, 1966, pp. 226-232.

Prausnitz 1986: Prausnitz, John M. - Lichtenthaler, Ruediger N. - de Azevedo, Edmundo G., Molecular thermodynamics of fluid-phase equilibria, Englewood Cliffs (N.J.), Prentice-Hall, 1986.

Rowlinson 1969: Rowlinson, John S., Liquids and liquid mixtures, 2. ed., London, Butterworths, 1969.

Sanchez, Panayiotou 1994: Sanchez, Isaac C. - Panayiotou, Christos G., Equation of state thermodynamics of polymer and related solutions, in: Model for thermodynamics and phase equilibria calculations, edited by Stanley I. Sandler, New York, Dekker, 1994.

Vera, Prausnitz 1972: Vera, Juan H. - Prausnitz, John M., Generalized van der Waals theory for dense fluids, "Chemical engineering journal", 3, 1972, pp. 1-13.

Whalen 1991: Whalen, James W., Molecular thermodynamics: a statistical approach, New York, Wiley, 1991.