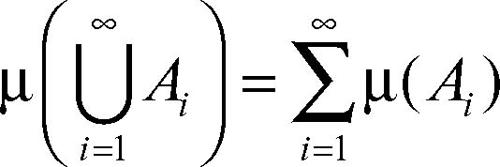misura, teoria della
misura, teoria della
misura, teoria della settore della matematica che studia le caratteristiche generali delle misure, estendendo le nozioni intuitive di lunghezza, area e volume a enti e situazioni del tutto generali. I più importanti esempi di misura sono la misura di → Lebesgue, la misura di → Peano-Jordan e la misura di → Borel. Un’ulteriore generalizzazione si ottiene definendo assiomaticamente lo spazio misurabile. Un insieme X dotato di una famiglia di sottoinsiemi S che costituiscono una σ-algebra (→ sigma-algebra) si dice spazio misurabile e gli elementi di S si chiamano insiemi misurabili. Si definisce allora misura una funzione µ definita su uno spazio misurabile (X, S) a valori nell’insieme dei numeri reali o complessi tale che:
• µ(Ø) = 0;
• se {Ai} è una collezione numerabile di elementi a due a due disgiunti di S, allora
L’ultima relazione si esprime anche dicendo che µ è numerabilmente additiva. Se µ è definita a valori in [0, +∞) si dice misura positiva. Se è definita a valori nell’insieme dei numeri complessi si dice misura complessa. Un insieme X dotato di una σ-algebra S e di una misura µ definita su S si dice spazio di misura (o spazio misurato).
Particolari spazi di misura sono gli spazi di probabilità nei quali l’insieme X rappresenta l’insieme degli eventi elementari, gli elementi di S rappresentano gli eventi casuali e la misura µ rappresenta la probabilità che si verifichi un certo evento. Quando una proprietà sussiste in tutti i punti di un insieme A, tranne eventualmente quelli formanti un insieme di misura nulla, si dice che la proprietà è verificata quasi ovunque in A. Una funzione definita quasi ovunque nell’insieme misurabile A si dice misurabile quando l’insieme dei punti x di A per cui ƒ(x) > c è misurabile o dotato di misura infinita per tutti i valori della costante c. Le funzioni continue sono misurabili; sono inoltre misurabili somme, prodotti, quozienti e limiti di successioni di funzioni misurabili nell’insieme misurabile A.