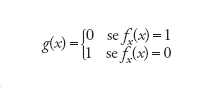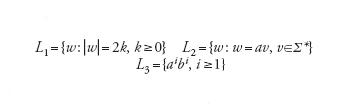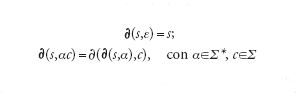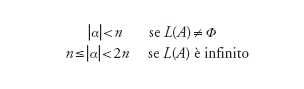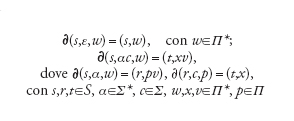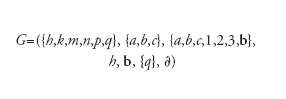Computazione, teoria della

Computazione, teoria della

La necessità del calcolo, pur riconosciuta dall'uomo in tutte le epoche storiche, ha condotto solo in tempi relativamente recenti a una sistemazione teorica della computazione. Due fatti hanno contribuito in modo determinante allo sviluppo di questi studi: da un lato la formalizzazione del concetto di procedura di calcolo, che possiamo datare al 1936; dall'altro lo sviluppo dei calcolatori a programma memorizzato. È questa l'origine dei due assi portanti della teoria della computazione, cioè la computabilità e la complessità di calcolo.

Il secondo problema di Hilbert sulla dimostrazione di compatibilità degli assiomi dell'aritmetica, posto all'inizio del XX sec. e rimasto insoluto anche nella formalizzazione dei Principia matematica di Bertrand Russell e Alfred N. Whitehead, aveva trovato una risposta negativa nel 1931 con il famoso teorema di incompletezza di Kurt Gödel, che provava l'esistenza di formule indimostrabili nel calcolo dei predicati del primo ordine. Questo teorema è basato sulla costruzione di una di tali formule e lascia aperto il problema della formalizzazione della procedura di dimostrazione, o più in generale della procedura di calcolo di una funzione. Gli anni che seguirono furono rivolti alla ricerca di tale formalizzazione, sotto l'ipotesi che ogni procedura dovesse consistere in una elencazione finita di operazioni elementari, ciascuna eseguibile meccanicamente in tempo finito. Nel 1936 Alan Turing introduceva la sua macchina (MT), che divenne il modello accettato di procedura e rimane tale per la sua equivalenza con ogni altro modello possibile, asserita nella ipotesi di Church. L'universalità del modello MT è anche suffragata dalla possibilità di definire una MT universale che simula il comportamento di ogni altra MT ed è equivalente agli altri modelli di macchina conosciuti, in particolare ai calcolatori se dotati di memoria sufficiente al calcolo richiesto.

La descrizione finita di algoritmo (o procedura) comporta come conseguenza che la classe di tutti gli algoritmi è numerabile, ovvero essi possono essere posti in corrispondenza biunivoca con i numeri naturali. Un modo pragmatico per convincersene è quello di formulare gli algoritmi stessi come programmi per un calcolatore ideale, elencarli in ordine alfabetico rispetto ai caratteri che li compongono e infine assegnare loro una numerazione progressiva: poichè si può banalmente dimostrare che i programmi ben formati sono infiniti, la classe dei programmi, e quindi degli algoritmi, ha la cardinalità degli interi.

Un argomento simile al precedente mostra che anche i dati su cui può operare un algoritmo, e i suoi risultati, rispondono a una descrizione finita e sono quindi numerabili. Ciò autorizza a considerare un algoritmo come meccanismo di calcolo di una funzione da ℕ su ℕ (cioè dai naturali sui naturali); e anzi lo studio può essere limitato agli algoritmi di decisione che calcolano funzioni da ℕ su {0,1} (decidono cioè se accettare o respingere un'asserzione rappresentata dai dati), poichè essi catturano tutte le proprietà interessanti della computabilità.

Questi fatti furono immediatamente posti in relazione alla non numerabilità della classe delle funzioni.

Infatti, se per esempio esistesse una numerazione f₀,f₁,…, per le funzioni da ℕ su {0,1} si potrebbe legittimamente costruire la funzione g tale che

[1] formula

per cui si avrebbe g(i)≠f_i(i) per ogni i∈ℕ. Scelta comunque una numerazione di tutte le funzioni, giungeremmo cioè alla contraddizione che g non fa parte dell'insieme.

La formalizzazione di algoritmo mise quindi in evidenza un fatto destinato a divenire uno dei cardini della teoria della computazione: poichè la classe delle funzioni non è numerabile ma quella degli algoritmi lo è, devono esistere funzioni per le quali non esiste procedimento di calcolo e cioè funzioni non calcolabili (o non decidibili nel caso di codominio {0,1}).

In sostanza non esiste un numero di algoritmi sufficiente a calcolare tutte le funzioni possibili. Se questo era in qualche misura atteso, molto meno ovvia fu l'individuazione delle prime funzioni non calcolabili corrispondenti a problemi matematici significativi e ben posti ma irrisolubili.

sommario

1. Notazione. 2. Automi finiti e linguaggi regolari. 3. Automi a pila e linguaggi liberi. 4. La macchina di Turing. 5. Decidibilità e indecidibilità. □ Bibliografia.

1. Notazione

La teoria degli algoritmi è interamente basata su descrizioni finite e discrete. L'intera disciplina può essere appresa su un numero finito di testi di lunghezza finita, composti unicamente con i caratteri (o simboli) di un insieme finito Σ detto alfabeto.

La notazione di base è quella della teoria degli insiemi. Si definiscono l'insieme vuoto Φ, le relazioni di appartenenza e di inclusione, le operazioni di unione, intersezione e differenza. La potenza 2^Σ dell'insieme Σ è l'insieme di tutti i sottoinsiemi di Σ. Il prodotto cartesiano Σ×Γ tra gli insiemi Σ e Γ è l'insieme di tutte le coppie ordinate (s,g) tali che s∈Σ, g∈Γ. Indichiamo gli alfabeti con lettere greche maiuscole e i loro caratteri con le prime lettere latine minuscole o con cifre numeriche.

Una stringa w su un alfabeto Σ è una sequenza finita di caratteri di Σ; la sua lunghezza ∣w∣ è il numero di caratteri che essa contiene. Il simbolo ε indica la stringa vuota e ovviamente ∣ε∣=0. Indichiamo le stringhe con le ultime lettere dell'alfabeto latino o con lettere greche, tutte minuscole. La concatenazione vw di due stringhe v e w è la stringa composta da v seguita da w. Per ogni stringa w si ha εw=wε=w. La stringa costituita da un carattere c ripetuto i≥0 volte si indica con cⁱ.

La stella Σ* di un alfabeto Σ è l'insieme (infinito) di tutte le stringhe sull'alfabeto, inclusa quella vuota. Un linguaggio L è un insieme finito o infinito di stringhe su Σ, cioè L∈Σ*. Il complemento ⌝L di un linguaggio L è definito come ⌝L=Σ*−L. I linguaggi si indicano specificando le proprietà che caratterizzano le loro parole, per esempio:

[2] formula

sono linguaggi su Σ={a, b, c} rispettivamente tutte e sole le stringhe che rispettivamente hanno un numero pari di caratteri (inclusa la stringa vuota), iniziano con a e iniziano con un numero arbitrario di a seguito dallo stesso numero di b.

Ovviamente Σ* è numerabile, ma non lo è la classe di tutti i linguaggi su Σ. Consideriamo ora un automa (o procedura) A che dà risposte su {0,1}. Detto Σ l'alfabeto con cui vengono rappresentati i dati d'ingresso, l'insieme di tutti i dati possibili è Σ* così che A calcola una funzione f da Σ* su {0,1}. Fissata un'arbitraria numerazione delle stringhe di Σ*, si può affermare che f è una funzione da ℕ su {0,1} e dunque che A realizza una delle procedure di decisione il cui studio, come già affermato, contiene i risultati chiave della teoria della computazione. Se L è il sottoinsieme di Σ* per cui A dà risposta 1, diremo che L è il linguaggio accettato da A. La computabilità può quindi essere vista come studio delle proprietà dei linguaggi accettati da diverse famiglie di automi, anche se l'intera questione sarà complicata dal fatto che l'automa potrebbe non fornire risposta in tempo finito.

Automi finiti e linguaggi regolari

Il primo modello di calcolo che prendiamo in considerazione è quello di automa finito (brevemente AF), definito come collezione di cinque entità (S,Σ,s′,F,∂) ove

S è un insieme finito di stati;

Σ è l'alfabeto d'ingresso;

s′∈S è lo stato iniziale;

F⊆S è l'insieme degli stati finali;

∂ è una funzione di transizione da S×Σ su S.

L'automa esegue una successione di mosse. Posto inizialmente nello stato s′, esso legge una stringa d'ingresso α∈Σ* un carattere per mossa e assume a ogni mossa un nuovo stato indicato dalla funzione di transizione: se l'automa si trova nello stato s∈S e legge il carattere c∈α‚ esso si porta nello stato ∂(s,c) e sposta la lettura sul carattere successivo di α. La stringa α è accettata se e solo se, con la lettura del suo ultimo carattere, l'automa si porta in uno stato finale f∈F.

Attraverso il meccanismo di transizione tra stati l'automa raccoglie e conserva informazione sullo svolgimento del calcolo, aggiornandola a ogni mossa sulla base dei caratteri di α. Ogni stato di S corrisponde alla memoria di una proprietà del prefisso di α che termina sull'ultimo carattere letto. Poichè Σ* è infinito e S è finito, vi sarà in genere un numero infinito di stringhe prefisso che conducono l'automa nello stesso stato, per le quali cioè l'automa riconosce e memorizza la stessa proprietà. In particolare una proprietà è associata a ogni stato finale, e caratterizza le stringhe accettabili.

tab. 1

La funzione di transizione si assegna indicandone i valori ∂(s,c) in una tabella di transizione in cui le righe corrispondono agli stati s e le colonne ai caratteri c. Consideriamo per esempio l'automa A=({s′,s₀,s₁,s₂}, {0,1}, s′, {s₀}, ∂), cui è associata la tabella di transizione (tab. 1). A accetta tutte e sole le stringhe di 0 e 1 che rappresentano numeri binari multipli di tre. Per esempio, la stringa 10010 (numero decimale 18) causa la sequenza di transizioni s′→s₁→s₂→s₁→s₀→s₀ che termina nello stato finale s₀ ed è quindi accettata da A. La stringa 1101 (codifica binaria di 13) causa invece le transizioni s′→s₁→s₀→s₀→s₁ e non è quindi accettata (tab. 1).

È utile estendere il dominio di definizione della funzione di transizione per designare il comportamento dell'automa in risposta a intere sequenze d'ingresso. Si introduce la nuova funzione ∂ da S×Σ* su S, definita ricorsivamente attraverso le relazioni:

[3] formula

Si definisce allora il linguaggio accettato da un automa finito M=(S,Σ,s′,F,∂) come l'insieme di stringhe L(M)={α tale che ∂(s′,α)∈F}. Un linguaggio (o insieme) L si dice regolare se esiste un automa finito M tale che L=L(M). Per l'automa A della tab. 1 abbiamo L(A)={α tale che [α]≡0 mod3, ∣α∣>0} e dunque questo linguaggio è regolare.

Un'importante modificazione dell'automa finito, che ritroveremo anche negli altri modelli di calcolo, è quella di automa finito non deterministico (brevemente AFND) M=(S,Σ,s′,F,∂′), ove per uno stesso stato e uno stesso carattere letto dall'esterno, si definiscono più mosse per M. Il significato di S, Σ, s′ e F rimane invariato, mentre la funzione di transizione ∂′ è ora definita da S×Σ su 2^S e cioè ∂′(s,c)=R⊆S, ove R è l'insieme di tutti gli stati in cui l'automa può portarsi dallo stato s leggendo il carattere c. Tutti questi stati devono essere provati dall'automa, che segue così una molteplicità di percorsi di calcolo paralleli in relazione a una stessa stringa d'ingresso. La stringa è accettata se e solo se almeno uno di questi percorsi termina in uno stato finale f∈F. Si noti che 2^S contiene l'insieme vuoto e quindi potrebbe esistere una coppia s,c per cui ∂′(s,c)=Φ: in questo caso la nuova mossa non è definita e il percorso di calcolo contenente s,c si arresta. Questa estensione non amplia la classe dei linguaggi regolari perché si dimostra:

Teorema 1. Se L è il linguaggio accettato da un AFND arbitrario, esiste un AF (deterministico) che accetta L.

Tra le numerose proprietà di cui godono i linguaggi regolari, le seguenti sono assai notevoli. La prima è nota come pumping lemma.

Lemma 2. Per ogni linguaggio regolare L esiste una costante n>0 tale che qualsiasi stringa α∈L, con ∣α∣≥n, può essere espressa come α=βγδ, con ∣βγ∣≤n e ∣γ∣≥1, in modo che la nuova stringa α′=βγⁱδ∈L per ogni i≥0.

Una conseguenza del lemma è la possibilità di decidere se il linguaggio L(A) accettato da un algoritmo finito A di n stati è vuoto, finito o infinito. Infatti L(A) deve contenere almeno una stringa α tale che

[4] formula.

Controllando la risposta di A su tutte le stringhe di lunghezza minore di n, o compresa tra n e 2n, si stabilisce se L(A) è vuoto o non vuoto, finito o infinito. Poichè tutte queste stringhe sono in numero finito e l'automa A risponde a ciascuna di esse in tempo finito, il procedimento accennato è effettivamente eseguibile (anche se molto inefficiente; ma ne esistono di più rapidi). La teoria della computazione studia diverse proprietà degli insiemi, ma annette particolare importanza a quelle per cui è nota una procedura di decisione.

I linguaggi regolari godono di varie proprietà di chiusura tra cui ricordiamo:

Teorema 3. La famiglia dei linguaggi regolari è chiusa sotto le operazioni di unione, intersezione e complemento. Inoltre, dati due AF A₁ e A₂, esistono (semplici) procedure per costruire un AF A₃tale che: L(A₃)==L(A₁)∪L(A₂); L(A₃)=L(A₁)∩L(A₂); L(A₃)=∉L(A₁).

Due automi che accettano lo stesso linguaggio si dicono equivalenti. Una conseguenza del precedente teorema è che si può costruire un automa A₄ che riconosce il linguaggio L(A₄)=(L(A₁)∩⌝L(A₂))∪(⌝L(A₁)∩L(A₂)), e si vede immediatamente che L(A₄)=Φ se e solo se L(A₁)=L(A₂). Poiché sappiamo che esiste una procedura per decidere se L(A₄)=Φ, possiamo concludere:

Teorema 4. Esiste una procedura per decidere se due automi finiti sono equivalenti.

Automi a pila e linguaggi liberi

La potenza di calcolo degli automi finiti è limitata dalla finitezza della memoria. Il ricordo di una situazione è infatti registrato unicamente nello stato assunto dall'automa, e poiché l'insieme degli stati è finito il numero di situazioni memorizzabili è anch'esso finito. Si accresce la potenza del modello ammettendo che l'automa conservi dimensioni finite ma che possa registrare su un mezzo esterno, detto pila, un numero a priori illimitato di situazioni diverse. La pila può contenere una stringa w di lunghezza illimitata composta di caratteri di un proprio alfabeto Π. L'accesso alla pila avviene sul primo carattere p di w (testa della pila), e ha lo scopo di leggere p e di memorizzare una nuova informazione mediante l'inserzione nella pila di una stringa x che sostituisce p. Posto w=py con p∈Π, y∈Π* e x∈Π*, l'inserzione di x causa la trasformazione della stringa contenuta nella pila da w a xy e il conseguente spostamento della testa sul primo carattere di x.

Definiamo allora l'automa a pila (AP) come collezione di sette entità (S,Σ,Π,s′,p′,F,∂) ove:

S è un insieme finito di stati;

Σ è l'alfabeto d'ingresso;

Π è l'alfabeto della pila;

s′∈S è lo stato iniziale;

p′∈Π è il carattere iniziale;

F⊆S è l'insieme di stati finali;

∂ è una funzione di transizione da S×Σ×Π su S×Π*.

Il funzionamento dell'AP è simile a quello dell'AF, fatta eccezione per l'impiego della pila. Esso è posto inizialmente nello stato s′, con pila contenente p′, e legge per scansione una stringa d'ingresso α∈Σ*. A ogni mossa l'automa si trova in uno stato s∈S, legge un carattere c∈α e il carattere p in testa alla pila; se ∂(s,c,p)=(t,x), con t∈S e x∈Π*, esso si porta nello stato t e inserisce x nella pila cancellandovi p; se invece ∂(s,c,p) non è definita, la computazione si arresta (∂ può non essere definita sull'intero dominio). La stringa α è accettata se e solo se, con la lettura del suo ultimo carattere, l'automa si porta in uno stato finale f∈F; in particolare α non è accettata se la computazione si arresta prima che la stringa sia letta completamente.

tab. 2

Anche ora la funzione ∂ si assegna elencandone i valori ∂(s,c,p) in una tabella di transizione, in cui le righe corrispondono agli stati s e le colonne alle coppie di caratteri c,p (tab. 2). Consideriamo per esempio l'automa B=({s₀,s₁,s₂,s₃}, {a,b}, {0,1}, s₀, 0, {s₃}, ∂} cui è associata la tabella di transizione della fig. 2. B accetta tutte e sole le stringhe del linguaggio L={aⁱbⁱ, i≥1} e si può facilmente dimostrare applicando il Lemma 2 che L non è regolare. Per esempio la stringa d'ingresso aaabbb causa la seguente sequenza di transizioni tra stati, con associati contenuti della pila: s₀,0→s₁,0→s₁,10→s₁,110→s₂,10→s₂,0→s₃, 0 che termina nello stato finale s3; la stringa è quindi accettata. La stringa aabbb si arresta invece sulla lettura dell'ultimo carattere, perché si dovrebbe applicare il valore non definito ∂(s₃,b,0): la stringa non è quindi accettata.

È di nuovo utile estendere il dominio di definizione della funzione ∂ per designare il comportamento dell'automa in risposta ad arbitrarie coppie di stringhe di ingresso e pila. Si introduce a tale scopo la funzione ∂ definita ricorsivamente come:

[5] formula.

Il linguaggio accettato da un AP M=(S,Σ,Π,s′,p′,F,∂) è allora l'insieme L(M)={α tali che ∂(s′,α,p′)=(f,w), f ∈F}. (Si noti che se risulta ∂(s,α,w)=(r,ε), si ha ∂(r,c,ε) indefinita e quindi ∂(s,αc,w) indefinita). Per l'automa B abbiamo L(B)={aⁱ bⁱ, i≥1}.

A differenza di quanto avviene per gli automi finiti, il non determinismo aumenta la potenza di calcolo del modello. Un automa a pila è non deterministico (APND) se, per uno stesso stato, uno stesso carattere d'ingresso e uno stesso carattere in testa alla pila si definiscono più mosse per M. Il significato di S, Σ, Π, s′, p′, F rimane invariato, mentre si ridefiniscono in modo facilmente immaginabile la funzione di transizione ∂ e la sua estensione ∂. Con la lettura di c,p l'automa apre r percorsidi calcolo distinti, e la stringa d'ingresso è accettatase e solo se almeno uno di questi percorsi termina in uno stato finale.

Un linguaggio L si dice libero se esiste un automa a pila M, deterministico o non, tale che L=L(M). Per esempio esiste un APND E tale che L(E)={αα^r, con α∈{a,b}*}, ove α^r indica la stringa inversa di α (cioè α^r letta da destra a sinistra coincide con α). Dunque questo linguaggio è libero. I linguaggi accettati dagli automi a pila deterministici costituiscono un sottoinsieme proprio dei linguaggi liberi: si può per esempio dimostrare che non esiste un AP che accetta il linguaggio L(E). I linguaggi regolari a loro volta costituiscono un sottoinsieme dei linguaggi accettati da AP, come si deduce immediatamente notando che ogni AF è un caso particolare di AP che non impiega la pila (ovvero ∂(s,c,p′)=(t,p) ovunque ∂ è definita). Inoltre tale sottoinsieme è proprio, come risulta da quanto provato sul linguaggio {aⁱ bⁱ, i≥1}. Tra i linguaggi liberi si trovano i principali linguaggi di programmazione, per cui la teoria degli automi a pila riveste importanza fondamentale nella interpretazione di programmi.

Riportiamo ora alcune delle numerosissime proprietà di cui godono i linguaggi liberi. Il seguente risultato è un'estensione del Lemma 2 già presentato per i linguaggi regolari:

Lemma 5. Per ogni linguaggio libero L esiste una costante n>0 tale che qualsiasi stringa α∈L, con ∣α∣≥n, può essere espressa come α=βγδζη, con ∣γδζ∣≤n e ∣γζ∣≥1, in modo che la nuova stringa α′=βγⁱδζⁱη∈L per ogni i≥0.

Una conseguenza del lemma è la possibilità di decidere se il linguaggio L(A) accettato da un AP o APND A è vuoto, finito o infinito, con test di lunghezza finita condotti sull'automa, in modo simile a quanto indicato per i linguaggi regolari. Si può inoltre riconoscere che un linguaggio L non è libero se si individua una stringa α∈L che, comunque suddivisa in βγδζη, genera una stringa α′∉L. Poniamo per esempio che il linguaggio L={aⁱbⁱcⁱ, i≥1} sia libero, e che n sia la costante del Lemma 5. La stringa α=aⁿbⁿcⁿ∈L potrebbe allora essere scritta secondo il lemma stesso come α=βγδζη, e in essa la sottostringa γδζ avrebbe lunghezza minore o uguale a n e quindi non potrebbe contenere contemporaneamente a e c. La stringa α′=βγⁱδζⁱη=βδη avrebbe allora un numero di a diverso dal numero di c, e non apparterrebbe a L in contrasto con il Lemma 5. Concludiamo che {aⁱbⁱcⁱ, i≥1} non è un linguaggio libero. Le proprietà di chiusura sono meno ricche per i linguaggi liberi che per quelli regolari. In particolare abbiamo:

Teorema 6. 1) La famiglia dei linguaggi liberi è chiusa sotto l'operazione di unione. Inoltre, dati due AP (o APND) A₁ e A₂, esiste una (semplice) procedura per costruire un AP (o APND) A₃ tale che L(A₃)=L(A₁)∪L(A₂).

2) La famiglia dei linguaggi liberi non è chiusa sotto le operazioni di intersezione e complemento. Inoltre, dati due AP (o APND) A₁ e A₂, non esiste una procedura per decidere se L(A₁)∩L(A₂), oppure ⌝L(A₁), sono linguaggi liberi (cioè se esiste un AP o APND che li accetta).

Il punto 2) del teorema afferma la non esistenza di una procedura di decisione per due quesiti posti sui linguaggi liberi, ovvero l'indecidibilità di tali quesiti. Abbiamo riconosciuto nel paragrafo 1 che devono esistere problemi indecidibili, e per provarlo sono necessari gli strumenti sviluppati nel prossimo paragrafo. Similmente si può dimostrare che vale un altro drastico risultato negativo per i linguaggi liberi, e cioè:

Teorema 7. Non esiste procedura per decidere se due arbitrari automi a pila A₁ e A₂ sono equivalenti (cioè se L(A₁)=L(A₂)).

La macchina di Turing

L'automa più potente dal punto di vista del calcolo fu introdotto da Turing nel 1936. Si tratta di una macchina astratta di dimensioni finite, dotata di un organo (testa) che scandisce le celle consecutive di un nastro esterno di lunghezza illimitata, su cui esegue operazioni di lettura e scrittura. Tale scrittura consente la memorizzazione sul nastro di un numero illimitato di eventi e la macchina può recuperare l'informazione registrata in qualsiasi posizione.

Formalmente la macchina di Turing (MT) si definisce come una collezione di sette entità (S,Σ,Π,s′,b,F,∂) ove:

S è un insieme finito di stati;

Σ è l'alfabeto d'ingresso;

Π è l'alfabeto del nastro, con Σ⊂Π;

s′ è lo stato iniziale;

b∈Π−Σ è un carattere speciale del nastro, detto bianco;

F⊆S è l'insieme di stati finali;

∂ è la funzione di transizione da S×Π su S×Π×{←,→}.

La funzione ∂ può non essere definita sull'intero dominio S×Π: in particolare non è definita su F×Π.

Il nastro ha un'origine ove si trova la sua prima cella ed è illimitato verso destra: inizialmente esso contiene una stringa d'ingresso α∈Σ* registrata a partire dalla prima cella, seguita da una stringa di b illimitata a destra. La macchina inizia a operare nello stato s′, con la testa posta sulla prima cella del nastro; in ogni istante essa si trova in uno stato s∈S, legge un carattere c∈Π dal nastro ed esegue una delle azioni seguenti:

a) se ∂(s,c)=(t,d,m), con t∈S, d∈Π e m∈{←,→}, la macchina si porta nello stato t, cancella c dal nastro e scrive al suo posto d, sposta la testa sul nastro di una posizione, a sinistra se m=← e a destra se m=→;

b) se ∂(s,c) non è definita, o se la testa si sposta a sinistra dell'origine del nastro, la macchina si arresta.

Il meccanismo di cancellazione e riscrittura sul nastro fa sì che la stringa iniziale αbbb… si trasformi via via in un'altra, composta con i caratteri di Π. La stringa α è accettata se la macchina si porta in uno stato f∈F, ove si arresta, in un numero finito di mosse: a questo punto il nastro contiene una stringa qualsiasi completata a destra da infiniti b, e la testa può trovarsi in una posizione qualsiasi del nastro. Se la macchina si arresta in uno stato di S−F o non si arresta mai, la stringa non è accettata.

La computazione eseguita da una MT fino a un dato istante è riassunta dallo stato raggiunto dalla macchina, il contenuto del nastro e la posizione della testa. Si definisce quindi la descrizione istantanea (DI) della macchina come la stringa xsy, con x,y∈Π* e s∈S, tale che:

1) s è lo stato della MT;

2) xy è la stringa contenuta nel nastro fino al carattere più a destra diverso da b, o, se la testa è entrata nella stringa illimitata di b, fino al carattere a sinistra della testa;

3) la posizione della testa sul nastro è indicata dalla posizione del simbolo s in DI: se y≠ε la testa si trova sul primo carattere di y, altrimenti si trova su un carattere della stringa illimitata di b.

Una mossa della MT consiste nel passaggio tra due DI, D₁ e D₂, e si indica col simbolo D₁∣−D₂. La computazione, per la stringa d'ingresso α‚ è una successione di mosse che partono dalla DI iniziale s′α. Consideriamo per esempio la macchina

[6] formula

tab. 3

la cui funzione ∂ è specificata nella tabella di transizione di tab. 3 ove il valore ∂(s,j) si trova in riga s, colonna j. G accetta tutte e sole le stringhe del linguaggio L={aⁱbⁱcⁱ, i≥0}, che abbiamo riconosciuto come non libero nel paragrafo precedente. Per esempio in risposta alla stringa d'ingresso aabbcc∈L la macchina esegue la computazione:

haabbcc ∣− 1kabbcc ∣− 1akbbcc ∣− 1a2mbcc ∣− 1a2bmcc 1a2nb3c ∣− 1an2b3c ∣− 1na2b3c ∣− n1a2b3c ∣− 1ha2b3c ∣− 11k2b3c ∣− 112kb3c ∣− 1122m3c ∣− 11223mc ∣− 1122n33 ∣− 112n233 ∣− 11n2233 ∣− 1n12233 ∣− 11h2233 ∣− 112p233 ∣− 1122p33 ∣− 11223p3 ∣− 112233p ∣− 112233bq

che si arresta nello stato finale q, poichè (q,b) non è definita, accettando la stringa. In risposta alla stringa abb∉L la computazione si arresta invece nello stato non finale p e la stringa non è quindi accettata.

Il passaggio tra due DI, D₁ e D₂, mediante un numero arbitrario di mosse consecutive si indica col simbolo D₁∣−*D₂, ove la relazione ∣−* è la chiusura riflessiva e transitiva di ∣−. Si definisce così il linguaggio accettato da una MT M come l'insieme L(M)={α tali che α∈Σ*, s′α∣−*xsy con s∈F, x,y∈Π*}. I linguaggi (o insiemi) accettati dalle MT si dicono ricorsivamente enumerabili. Per la MT G abbiamo L(G)={aⁱbⁱcⁱ, i≥0}, quindi questo linguaggio è ricorsivamente enumerabile.

Ricordiamo che una MT M si arresta per tutte le stringhe di L(M), mentre può arrestarsi o non arrestarsi per le stringhe non in L(M). Non esiste però in genere un limite superiore al numero di mosse necessarie a M per accettare una stringa, e perciò non esiste criterio generale per stabilire se una computazione in corso su una stringa d'ingresso α terminerà o no. Vi sono ovviamente MT che si arrestano su ogni stringa accettata o non accettata, come per esempio la G della tab. 3, ma come vedremo nel prossimo paragrafo non tutti i linguaggi ricorsivamente enumerabili sono accettati da macchine di questo tipo: vi sono quindi linguaggi ricorsivamente enumerabili per cui non è possibile stabilire, entro un tempo fissato a priori, l'appartenenza di una stringa arbitraria a essi.

Questa grave e inevitabile limitazione giustifica l'introduzione di un nuovo concetto: un linguaggio (o insieme) L si dice ricorsivo se esiste una MT M che si arresta sempre in tempo finito e tale che L=L(M). Per esempio il linguaggio {aⁱbⁱcⁱ, i≥0} è ricorsivo, perché è accettato dalla macchina G. Da quanto affermato dobbiamo concludere che i linguaggi ricorsivi sono un sottoinsieme proprio dei linguaggi ricorsivamente enumerabile.

La costruzione di una MT per il riconoscimento di un linguaggio dato L è sempre piuttosto complessa anche se L è molto semplice. Sono allora stati studiati diversi ampliamenti del modello che sono più comodi da impiegare ma che non ne aumentano la potenza di calcolo, ovvero la famiglia dei linguaggi accettati. In particolare abbiamo:

Teorema 8. Sia L il linguaggio accettato da una estensione X di una MT ottenuta:

1) con nastro illimitato verso destra e verso sinistra; oppure:

2) con k teste che agiscono contemporaneamente e indipendentemente sul nastro;

oppure:

3) con k teste che agiscono contemporaneamente e indipendentemente su k nastri indipendenti.

Allora esiste una MT Y che accetta L.

Teorema 9. Sia X un qualsiasi calcolatore elettronico esistente, corredato di memoria illimitata e di un programma per l'accettazione di stringhe (che abbia cioè uscita 0 o 1); sia inoltre L l'insieme di stringhe accettate da X. Allora esiste una MT Y che accetta L.

Anche nel caso presente è significativo definire una macchina di Turing non deterministica (brevemente MTND) che, per lo stesso stato e lo stesso carattere letto sul nastro, può eseguire più mosse. Il significato di S, Σ, Π, s′, b, F resta invariato, mentre la funzione di transizione è ora definita come ∂′ da S×Π su 2^{S×Π{←,→}}. Una stringa α è accettata in t mosse se almeno una delle computazioni per α raggiunge uno stato finale e la più breve tra tali computazioni consiste di t mosse. Nonostante l'apparente potenziamento del modello, la famiglia dei linguaggi accettati non cambia. Abbiamo infatti:

Teorema 10. Per ogni MTND X esiste una MT Y tale che L(X)=L(Y). Inoltre una stringa α accettata da X in t mosse è accettata da Y in t′>k^t-1 mosse, con k costante.

La dimostrazione del teorema è basata su una simulazione del funzionamento della MTND X sulla Y. Ammettendo che ogni mossa sia eseguita in tempo costante, i valori t e t′ del teorema possono essere presi come tempi di esecuzione di X e Y per le stringhe accettate.

Poiché il non determinismo non amplia la classe dei linguaggi accettati, gli studi di computabilità si conducono sulle MT (deterministiche). Il numero di mosse cresce esponenzialmente nella simulazione di una MTND X su una MT Y, ma ciò non esclude l'esistenza di una MT Y′ che accetti lo stesso linguaggio in un numero di mosse inferiore a quello richiesto da Y: quest'ultimo quesito, ancora irrisolto, è esaminato in profondità nell'ambito degli studi sulla complessità di calcolo.

Decidibilità e indecidibilità

Un problema ben posto deve avere una descrizione univoca, essere definito per uno o più dati e richiedere per essi un risultato. Da un punto di vista del calcolo il problema è significativo se i dati possono assumere infiniti valori, ciascuno dei quali rappresenta un'istanza del problema, e il risultato più di uno. Se infatti il numero di istanze fosse finito, la computazione potrebbe ridursi alla consultazione di una tabella finita che listi i valori del risultato in funzione dei valori dei dati; né è significativo il caso in cui il risultato assuma un solo valore, perché una volta noto per un'istanza non sarebbe più necessario calcolarlo per le altre. Invece, come abbiamo già affermato, ha senso limitare lo studio a problemi di decisione che non chiedono in genere di determinare una soluzione del problema, ma solo di verificare l'esistenza di una che possieda una proprietà specifica. Un esempio di problema di decisione con infinite istanze è P_sod, introdotto nel paragrafo precedente. L'istanza generica è un'espressione E, il risultato è l'esistenza o meno di un insieme di valori delle variabili che soddisfi la E. Il procedimento indicato per risolvere P_sod scopre l'esistenza di una soluzione generandola esplicitamente, ma ciò di norma non è richiesto.

Codificate le istanze di un problema di decisione P come stringhe su un alfabeto, il linguaggio L relativo a P è l'insieme delle istanze che prevedono risultato affermativo. Un procedimento di risoluzione di P può essere formalizzato come una MT M tale che L=L(M). Possiamo quindi trasformare il quesito sull'esistenza di una procedura effettiva di calcolo per P in uno equivalente sulla natura di L. Se L è ricorsivo, esiste una procedura che genera sempre in tempo finito una risposta affermativa o negativa. In tal caso il problema P è decidibile, e una MT che lo risolve è detta algoritmo per P. Se L non è ricorsivo il problema è indecidibile e non ammette algoritmo di risoluzione: tra questi problemi dobbiamo però distinguere quelli corrispondenti a linguaggi ricorsivamente numerabili o viceversa, poiché per i primi esiste una MT che può non fornire tutte le risposte in tempo finito mentre per i secondi la MT non esiste del tutto. Se le stringhe d'ingresso a una MT si interpretano come codifica di numeri naturali, la risoluzione di P corrisponde al calcolo di una funzione da ℕ su {0,1}: problemi decidibili o indecidibili corrispondono allora a funzioni calcolabili o non calcolabili.

Le MT sono definite come collezione di entità finite (S,Σ,Π,s′,b,F,∂) e possono quindi essere descritte come stringhe di un alfabeto arbitrario (in particolare è sufficiente l'alfabeto {0,1}). Tali stringhe possono poi essere ordinate alfabeticamente per lunghezza crescente, dando luogo a un'enumerazione delle MT nella quale la macchina M_i corrisponde all'i-esima stringa dell'ordinamento. Similmente si possono enumerare le stringhe d'ingresso α per le MT, indicando con α_i la stringa i-esima. Indicheremo con 〈M> la stringa che descrive la MT M, con 〈M,α> la stringa che descrive M assieme a una sua stringa d'ingresso α. Sarà allora legittimo impiegare 〈M,α> come stringa d'ingresso di una diversa MT N, per rispondere a questioni circa il comportamento di M su α. In particolare N potrà simulare il funzionamento di M, svolgendo quindi la funzione di un calcolatore che esegue un programma M sui dati α.

L'argomento di conteggio sulla numerabilità delle procedure e la non numerabilità delle funzioni, introdotto nel primo paragrafo, può ora essere formalmente ripreso in relazione alla numerazione delle MT. Si dimostra così che devono esistere funzioni non calcolabili perché per esse non vi è MT, ovvero devono esistere problemi indecidibili cui corrispondono linguaggi non ricorsivamente enumerabili. Il primo di questi linguaggi, detto linguaggio diagonale (L_d), è composto da tutte le stringhe α_i che non sono accettate dalla MT M_i di pari indice.

Teorema 11. Il linguaggio L_d={α_i tali che α_i∉L(M_i), i=0,1,…} non è ricorsivamente enumerabile.

Il teorema si dimostra notando che se esistesse una MT M_j tale che L_d=L(M_j), la definizione di L_d condurrebbe alla contraddizione che α_j∈L_d se e solo se α_j∉L(M_j). La scoperta che L_d non è ricorsivamente enumerabile permette di dimostrare l'indecidibilità di altri problemi, determinando la natura dei nuovi linguaggi in funzione della natura di L_d. Il primo di essi è relativo alla possibilità di stabilire se una MT arbitraria M accetta una stringa arbitraria α.

Teorema 12 (Turing). Il linguaggio L_u={〈M,α>: α∈L(M)} è ricorsivamente enumerabili e non è ricorsivo.

L_u è detto linguaggio universale poiché pone la più generale delle questioni sulle macchine di Turing; la sua natura dimostra che i linguaggi ricorsivi sono un sottoinsieme proprio dei linguaggi ricorsivamente enumerabili. In termini concreti il teorema afferma che non esiste algoritmo per stabilire il risultato di una computazione arbitraria (si noti che l'algoritmo non può in genere consistere nella simulazione di tale computazione, perché nel caso α∉L(M) la simulazione potrebbe non terminare in tempo finito). Una conseguenza del Teorema 12 è che anche il linguaggio L_a={〈M,α> tali che la computazione di M su α si arresta} è ricorsivamente enumerabile e non è ricorsivo. Questo famoso risultato decreta l'indecidibilità del problema dell'arresto (P_a), ovvero stabilisce che non esiste algoritmo per decidere se una computazione arbitraria si arresta o meno.

I problemi indecidibili fin qui considerati pongono domande sulle MT ma non sui linguaggi ricorsivamente enumerabili che esse accettano: questioni, queste ultime, assai più generali. Per esempio i due linguaggi:

[7] formula

appaiono simili, ma si ha L₁⊂L₂ poiché il fatto che in L₂ il linguaggio L(M) sia ricorsivo implica che esiste una MT M′ che lo accetta e si arresta sempre, ma non implica che sia M′=M: è infatti possibile costruire una M che si arresta esattamente per le stringhe α∈L(M) e non si arresta per le altre. Per le questioni inerenti i linguaggi ricorsivamente enumerabili vale un risultato molto generale, con numerose conseguenze:

Teorema 13 (Rice). Qualsiasi proprietà dei linguaggi ricorsivamente enumerabili è indecidibile, a meno che non sia banalmente verificata da tutti o da nessuno.

Corollario. Per un'arbitraria MT M le seguenti questioni sono indecidibili:

L(M)=Φ L(M)≠Φ,

L(M) è finito L(M) Σ*,

L(M) è regolare L(M) è libero,

L(M) è ricorsivo L(M) non è ricorsivo.

Per concludere accenniamo solo a due conseguenze che la teoria della decidibilità ha nell'ambito delle applicazioni. Sarebbe utile poter inserire un programma filtro all'ingresso di un calcolatore, per decidere, prima di iniziare l'esecuzione di un programma arbitrario se questo terminerà la sua computazione o entrerà in un ciclo infinito. L'indecidibilità del problema dell'arresto P_a dimostra che tale filtro non può esistere. Sarebbe inoltre importante poter stabilire se due programmi A₁ e A₂, scritti per esempio per calcolatori diversi, generano risultati uguali per uguali dati. Ciò ha corrispettivo nel problema dell'equivalenza P_e tra MT, anch'esso indecidibile: non esiste dunque un algoritmo per decidere se due programmi sono equivalenti.

bibliografia

Ausiello 1975: Ausiello, Giorgio, Complessità di calcolo delle funzioni, Torino, Boringhieri, 1975.

Börger 1985: Börger, Egon, Berechenbarkeit, Komplexität, Logik, Braunschweig, Vieweg, 1985.

Davis 1958: Davis, Martin, Computability and unsolvability, New York, McGraw-Hill, 1958.

Davis, Weyuker 1983: Davis, Martin - Weyuker, Elaine, Computability, complexity and languages, New York, Academic Press, 1983.

Hopcroft, Ullman 1979: Hopcroft, John E. - Ullman, Jeffery D., Introduction to automata theory, languages and computation, Reading (Mass.), Addison-Wesley, 1979.

Lewis, Papadimitriou 1981: Lewis, Harry R. - Papadimi-triou, Christos H., Elements of the theory of computation, Englewood Cliffs (N.J.), Prentice-Hall, 1981.

Rogers 1967: Rogers, Hartley jr, The theory of recursive functions and effective computability, New York, McGraw-Hill, 1967.

Salomaa 1985: Salomaa, Arto, Computation and automata, Cambridge, Cambridge University Press, 1985.