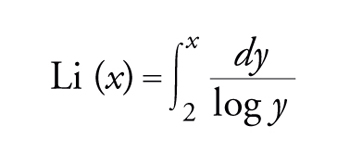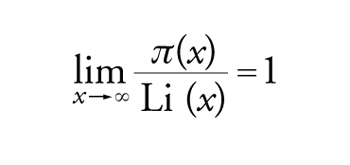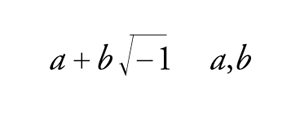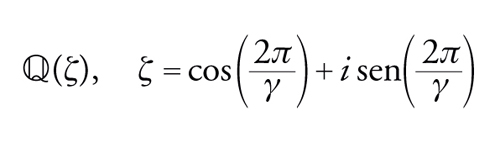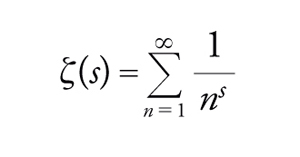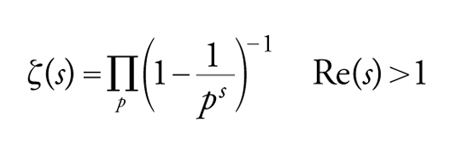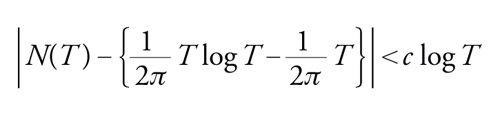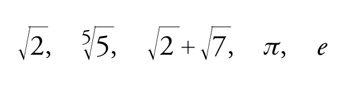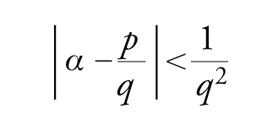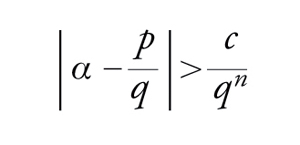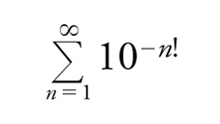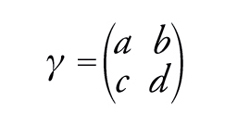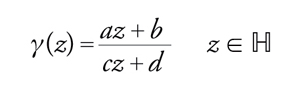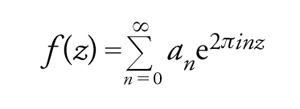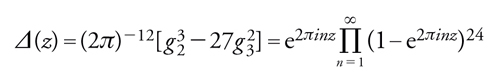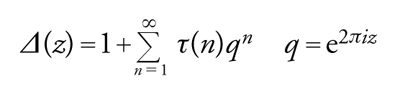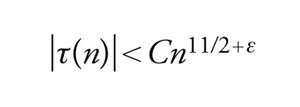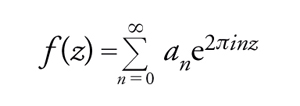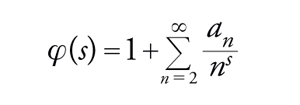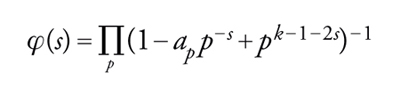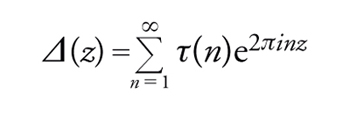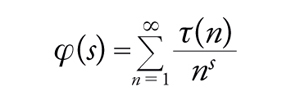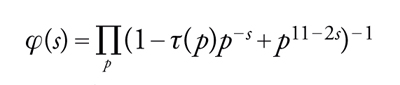Numeri, teoria dei

Numeri, teoria dei

La teoria dei numeri è il settore della matematica dedicato allo studio delle proprietà degli interi, cioè dell'insieme ℤ costituito dai numeri

…, −4, −3, −2, −1, 0, 1, 2, 3, 4, …

La teoria dei numeri si occupa anche delle proprietà dei vari sistemi algebrici che generalizzano gli interi, in particolare degli anelli di interi dei corpi di numeri algebrici. Questi sistemi algebrici emergono in modo naturale nello studio di molti problemi concernenti gli interi stessi.

Benché la teoria dei numeri sia attualmente un argomento tanto vasto da toccare quasi tutti gli altri settori della matematica, è possibile enucleare pochi argomenti fondamentali che sono stati i punti focali da cui si sono diramate le moderne linee di ricerca su di essa.

Equazioni diofantee

Un'equazione diofantea è un'equazione polinomiale in un qualsiasi numero di variabili di cui si vogliono determinare le soluzioni intere.

Le equazioni diofantee derivano il loro nome da Diofanto di Alessandria (250 a.C.), il cui trattato Arithmetica fu il primo studio sistematico di tali equazioni, ma in realtà erano state considerate centinaia di anni prima. Per esempio, la soluzione dell'equazione diofantea lineare ax+by=c, con a,b,c interi assegnati, è presente negli Elementi di Euclide.

Una famosa equazione diofantea è la cosiddetta equazione pitagorica:

[2] x²+y²=z².

Risolverla è equivalente a determinare tutti i triangoli rettangoli aventi lati di lunghezza intera. Tutte le sue soluzioni sono date da

[3] x=±2abc, y=±(a²−b²)c, z=±(a²+b²)c

dove a,b,c sono interi generici ed è permessa ogni combinazione di segni.

In generale, determinare le soluzioni intere di un'equazione è molto più sottile che determinarne le soluzioni reali o complesse e per questa ragione, benché lo studio delle equazioni diofantee sia vecchio di migliaia di anni, rimangono ancora vuoti considerevoli nelle nostre conoscenze. Anche oggi, il problema della loro risoluzione è uno dei temi centrali della teoria dei numeri.

La distribuzione dei primi

Un numero primo è un intero maggiore di 1 che non ha altri divisori positivi che 1 e se stesso. I più piccoli primi sono

[4] 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

La distribuzione dei primi tra gli interi è apparentemente priva di 'ordine' e fin dall'antichità si sono compiuti sforzi per determinare eventuali regolarità. Negli ultimi due secoli, questi sforzi hanno dato frutti originando la branca nota come teoria analitica dei numeri.

Teoria algebrica dei numeri

Se n è un intero diverso da 0 e ±1, allora può essere scritto nella forma n=±p₁×…×p_t, dove p₁,…,p_t sono primi. Una cosa meno ovvia, ma ben più importante, è il fatto che a meno dell'ordine i primi p₁,…,p_t sono determinati da n in modo unico. Quest'ultima asserzione è chiamata teorema fondamentale dell'aritmetica ed è un ingrediente chiave nella dimostrazione delle proprietà degli interi.

Lo studio di varie equazioni diofantee suggerisce una fattorizzazione simile degli interi anche in sistemi algebrici più generali. In tali casi l'analogo del teorema fondamentale dell'aritmetica può venir meno. Lo studio della mancanza di una fattorizzazione unica porta alla teoria algebrica dei numeri.

Congruenze. Siano x e y interi, n un intero positivo. Si dice che x è congruo a y modulo n, e si scrive x≡y (mod n), se x−y è divisibile per n. Un certo numero di fatti interessanti concernenti la divisibilità degli interi può essere formulato più chiaramente in termini di congruenze.

Le congruenze sono d'importanza centrale nella teoria dei numeri grazie alla possibilità di manipolarle per molti versi come se fossero equazioni. Esse forniscono quindi uno strumento di natura algebrica nello studio delle proprietà di divisibilità degli interi. Uno dei problemi più importanti concernenti le congruenze è quello di determinare le soluzioni di una congruenza polinomiale per polinomi a coefficienti interi.

La teoria dei numeri da Fermat a Gauss

Benché molti risultati particolari di teoria dei numeri fossero noti agli antichi, la storia di questa disciplina comincia con il lavoro del matematico francese Pierre de Fermat. I problemi da lui sollevati erano decisamente moderni. Uno di questi era il cosiddetto problema dei due quadrati, che consiste nello stabilire quali interi n possano essere scritti come somma di due quadrati. In altri termini, per quali n è risolubile l'equazione diofantea x²+y²=n? Fermat dette la soluzione seguente.

Teorema 1. Un intero positivo n può essere scritto come somma di due quadrati se e solo se n è della forma n=m²p₁…p_t, dove m è un intero e p₁,…,p_t sono primi distinti ognuno dei quali è 2 oppure è congruo a 1(mod 4). In particolare i primi che possono essere scritti come somma di due quadrati sono precisamente 2 e i primi congrui a 1(mod 4). Così per esempio, 5≡1(mod 4) e quindi 5 è somma di due quadrati: 5=2²+1²; viceversa 7≡3(mod 4), cosicché 7 non è rappresentabile in questa forma.

In apparente contrasto al risultato sulla rappresentabilità come somma di due quadrati, Fermat stabilì il teorema seguente.

Teorema 2. Ogni intero positivo è somma di quattro quadrati.

Egli affermò anche di aver dimostrato che l'equazione diofantea

[5] x²−Dy²=1

ammette infinite soluzioni, purché D sia un intero che non è un quadrato perfetto.

Senza dubbio l'asserzione più famosa di Fermat è stata la nota contenuta nella sua copia dell'Arithmetica di Diofanto circa il fatto che l'equazione diofantea

[6] xⁿ+yⁿ=zⁿ n≥3

non ha soluzioni intere non nulle x,y,z.

La prima dimostrazione del teorema 2 venne data da Joseph-Louis Lagrange nel 1770, dopo alcuni tentativi infruttuosi di Leonhard Euler. Quest'ultimo fu il primo a dimostrare l'esistenza di infinite soluzioni dell'equazione diofantea [5], che inspiegabilmente chiamò equazione di Pell.

Preminente tra i teorici dei numeri fu Carl Friedrich Gauss. Il suo lavoro unificò e consolidò i risultati del XVIII sec. e indicò la strada alle ricerche di teoria dei numeri per più di un secolo.

Nel 1799 egli completò il suo capolavoro, le Disquisitiones arithmeticae, il libro che più ha influito sulla teoria dei numeri nel XIX secolo. In esso Gauss ha introdotto la notazione moderna per le congruenze e ha proceduto a uno studio sistematico delle loro proprietà. Uno dei suoi obiettivi, solo parzialmente raggiunto, è stato lo studio esauriente della risolubilità della congruenza polinomiale

[7] aⁿxⁿ+a_n−1xⁿ−1+…+a₀≡0 (mod p)

dove p è un primo dispari e a₀,…,a_n sono interi assegnati.

Nel caso n=2 invece egli riportò un successo completo provando la legge di reciprocità quadratica. Gauss ne rimase affascinato e finì col darne sette dimostrazioni diverse. Uno degli aspetti sorprendenti è che essa lega la risolubilità della congruenza x²≡q (mod p) a quella della congruenza x²≡p (mod q). Usandola è anche possibile determinare se

[8] a₂x²+a₁x+a₀≡0 (mod p)

è risolubile o meno.

Oltre alla teoria delle congruenze, le Disquisitiones sviluppano una teoria generale delle equazioni diofantee quadratiche della forma

[9] ax²+bxy+cy²=n.

Un polinomio quadratico omogeneo ax²+bxy+cy² è chiamato forma quadratica binaria. Il lavoro di Gauss sull'argomento affronta due problemi principali: (a) se a,b,c e n sono assegnati, determinare tutte le soluzioni (x,y) dell'equazione diofantea [9]; (b) se a,b,c, sono assegnati, determinare tutti gli n per cui la [9] è risolubile. Il primo include come caso particolare la determinazione di tutte le soluzioni dell'equazione di Pell e con esso Gauss riportò un pieno successo. Egli ottenne invece solo risultati parziali nell'affrontare il secondo, che fornirebbe anche una risposta al problema dei due quadrati di Fermat e resta tuttora non completamente risolto.

In aggiunta al suo lavoro sulle congruenze e sulle forme quadratiche, Gauss portò a termine un lavoro fondamentale sulla distribuzione dei primi. Mostrando un'incredibile abilità di calcolo, fin dal 1792 (all'età di 15 anni) si mise a tabulare il numero di primi nei vari intervalli di lunghezza mille. Alla fine, i suoi calcoli si estesero a tutti i primi fino a tre milioni. Sulla base dell'evidenza numerica, Gauss congetturò che il numero dei primi minori di x, usualmente indicato con π(x), è dato approssimativamente dal cosiddetto logaritmo integrale,

[10] formula,

dove l'approssimazione è intesa nel senso che

[11] formula.

L'equazione [11] è nota come teorema dei numeri primi. Benché Gauss fosse stato il primo a ipotizzarne la validità, egli non pubblicò mai le sue ricerche.

Questa e altre congetture furono pubblicate da Adrien-Marie Legendre nel 1798. Esse andavano più in là di quelle di Gauss e consideravano il problema dei primi nelle progressioni aritmetiche. Più precisamente, Legendre si domandò inoltre se esistono infiniti primi nella progressione aritmetica

[12] k, k+l, k+2l, k+3l, …

dove k e l sono interi positivi senza fattori comuni maggiori di 1.

Il lavoro di Gauss pose le fondamenta per gran parte della teoria dei numeri del XIX e XX secolo. La legge di reciprocità quadratica precorreva leggi di reciprocità molto più generali, culminanti nella legge di reciprocità di Artin della teoria del corpo di classi. La sua teoria delle forme quadratiche binarie ha condotto alla teoria dei corpi di numeri algebrici e una parte delle sue ricerche sulle congruenze fornisce i primi esempi dell'ipotesi di Riemann per le curve. Inoltre il suo studio della distribuzione dei numeri primi è stato tra quelli che hanno dato vita alla teoria analitica dei numeri.

Infine, alcuni dei problemi posti da Gauss per primo sono stati risolti solo di recente mentre altri sembrano ben oltre la portata dei metodi attuali.

Teoria algebrica dei numeri

Nel XIX secolo si comprese presto che i numeri irrazionali avrebbero potuto essere usati sistematicamente per ottenere dei risultati concernenti gli interi. Per esempio, ancora Gauss notò che la fattorizzazione

[13] formula

collega l'insieme dei numeri complessi della forma

[14] formula

interi,

con il problema dei due quadrati. I numeri del tipo [14] sono chiamati interi di Gauss. Poiché la loro somma, differenza e prodotto sono di nuovo un intero di Gauss, questi formano un sistema algebrico molto simile agli interi ordinari, al cui interno è possibile sviluppare una teoria della fattorizzazione. Ogni intero di Gauss α≠0 ha per fattori ±1, ±i, ±α e ±iα, dove i=√−1. Se questi sono gli unici fattori e α è diverso da ±1 e ±i, allora α è chiamato primo di Gauss. Per gli interi di Gauss vale il seguente analogo del teorema fondamentale dell'aritmetica.

Teorema 3. Sia α≠0, ±1, ±i un intero di Gauss. Allora α può essere scritto nella forma α=π₁…π_t, dove π₁,…,π_t sono primi di Gauss. Inoltre, π₁,…,π_t sono unicamente determinati da α, a meno dell'ordine e della moltiplicazione per ±1 e ±i.

Corpi di numeri algebrici

Se un numero complesso α è una radice di una equazione polinomiale f(α)=0, dove f(x)=xⁿ+a₁xⁿ−1+…+a_n ha coefficienti razionali, allora α è chiamato numero algebrico. Se inoltre tutti gli a_i sono interi, allora α è chiamato intero algebrico. È facile vedere che se α è contemporaneamente razionale e intero algebrico, allora è un intero ordinario. Quindi la nozione d'intero algebrico generalizza il concetto d'intero ordinario.

Supponiamo ora che α sia un numero algebrico. Allora esiste un unico polinomio f(x)=xⁿ+a₁xⁿ−1+…+a_n a coefficienti razionali irriducibile sui razionali che ha α come zero. L'intero n è detto il grado di α e f(x) è detto il polinomio minimo di α. Indichiamo con F l'insieme di tutti i numeri della forma

[15] ϑ=x₀+x₁α+x₂α²+…+x_n−1αⁿ−1 x_i razionali.

La somma, la differenza, il prodotto e il quoziente di elementi di F appartiene ancora a F, sicché F è un corpo. Un corpo ottenuto in questo modo è chiamato corpo di numeri algebrici. Ogni elemento di F può essere scritto in modo unico nella forma [15]. L'intero n è detto il grado di F.

Esempi di corpi di numeri algebrici sono i seguenti:

Corpi quadratici. Sia d un intero non divisibile per il quadrato di qualunque intero maggiore di 1. Allora α=√d è radice del polinomio irriducibile f(x)=x²−d. Il corrispondente corpo di numeri algebrici, indicato con ℚ(√d), consiste di tutti i numeri della forma x₀+x₁√d, con x₀,x₁ razionali. Il grado di ℚ(√d) è 2.

Corpi ciclotomici. Sia p un primo dispari, α=ζ==cos(2π/p)+i sen(2π/p) una radice p-esima primitiva dell'unità. Allora α è una radice del polinomio irriducibile f(x)=x^p−1+x^p−2+…+x+1. Il corrispondente corpo di numeri algebrici consiste di tutti i numeri della forma

[16] x₀+x₁ζ+x₂ζ²+…+x_p−2ζ^p−2 x_i razionali

ed è indicato con ℚ(ζ). Il grado di ℚ(ζ) è p−1.

Sia ora F un qualunque fissato corpo di numeri algebrici. L'insieme di tutti gli interi algebrici di F è un anello ed è indicato con O_F. L'aritmetica dell'anello O_F è il principale oggetto di studio nel campo della teoria algebrica dei numeri.

Il concetto di ideale

La connessione tra corpi di numeri algebrici ed equazioni diofantee costituisce un forte incentivo per lo sviluppo di una teoria della fattorizzazione per l'anello degli interi algebrici di un arbitrario corpo algebrico. Sfortunatamente, per quanto riguarda la fattorizzazione in un anello d'interi algebrici le cose vanno in maniera assai più complicata che per gli interi ordinari.

Un'unità di O_F è un elemento ε di O_F tale che ε⁻¹ appartiene a O_F. Per esempio, le unità di ℤ sono ±1, quelle degli interi di Gauss ±1, ±i mentre nel caso F=ℚ(√2) le unità di O_F sono ±(1+√2)ⁿ, con n intero generico. Se α∈O_F ha una fattorizzazione α=βγ, allora, per ogni unità ε, è possibile fattorizzare α come (βε)(γε⁻¹). Così, le unità di O_F creano una certa ineliminabile quantità di non unicità nella fattorizzazione. Un elemento α di O_F è detto irriducibile se non è né zero né un'unità e i soli fattori di α sono della forma ε o εα, con ε unità di O_F. In particolare gli elementi irriducibili di ℤ sono quelli della forma ±p, con p primo e gli elementi irriducibili degli interi di Gauss sono i primi di Gauss. È facile vedere che ogni α in O_F che non è né zero né un'unità può essere scritto come prodotto di elementi irriducibili, α=π₁…π_t. Si dice che O_F è un dominio a fattorizzazione unica se π₁,…,π_t sono determinati in modo unico da α, a meno dell'ordine e della moltiplicazione per un'unità.

Nel corso delle sue ricerche sull'ultimo teorema di Fermat, Ernst E. Kummer introdusse certi numeri ideali che giocano il ruolo di massimi comun divisori degli interi algebrici. Per spiegare la teoria di Kummer, conviene adottare il punto di vista del suo successore Richard Dedekind e introdurre il concetto di ideale.

Un ideale di O_F è una collezione I di elementi di O_F tale che: (a) I contiene almeno un elemento non nullo; (b) se α, β appartengono a I anche α±β appartengono a I; (c) se α appartiene a I e β appartiene a O_F, allora αβ appartiene a I. Se α è un elemento non nullo di O_F, allora l'insieme (α) costituito dai numeri αβ, con β in O_F, è un ideale, in questo caso chiamato ideale principale. Tutti gli ideali di ℤ sono principali, sicché possono essere visti essenzialmente come analoghi dei numeri interi. Tuttavia, per un generico corpo F non tutti gli ideali di O_F sono necessariamente principali. In questo caso, gli ideali sono una specie di numeri addizionali associati a O_F, che compensano la non unicità nella fattorizzazione dei suoi elementi. Si può infatti dimostrare il seguente

Teorema 4. O_F è un dominio a fattorizzazione unica se e solo se ogni ideale di O_F è principale.

L'idea basilare della teoria degli ideali è di sostituire l'aritmetica degli elementi di O_F con l'aritmetica degli ideali di O_F. È possibile definire il prodotto I₁∙I₂ di ideali I₁,I₂ in modo tale che il prodotto di due ideali principali (α) e (β) sia esattamente (αβ), così da estendere la nozione di moltiplicazione di numeri.

Gli ideali possono inoltre essere fattorizzati in maniera del tutto analoga ai numeri. Un ideale P di O_F viene detto ideale primo se ogni fattorizzazione di P è banale, cioè se P=I₁I₂ implica che o I₁=P, I₂=O_F oppure I₂=P, I₁=O_F. Benché O_F sia solo raramente un dominio a fattorizzazione unica, gli ideali di O_F si fattorizzano in modo unico. Più precisamente, vale il risultato seguente.

Teorema fondamentale della teoria degli ideali. Sia A un ideale di O_F. Allora A può essere scritto nella forma P₁…P_t, dove P₁,…,P_t sono ideali primi. Inoltre P₁,…,P_t sono unicamente determinati da A, a meno dell'ordine.

In molti problemi di teoria dei numeri, la fattorizzazione unica degli ideali può sostituire utilmente la fattorizzazione unica dei numeri.

Aritmetica nei corpi di numeri

Decomposizione dei primi. Sia F un corpo di numeri algebrici e sia p un primo ordinario. Allora pO_F è un ideale di O_F e pertanto, in virtù del teorema fondamentale,

[17] pO_F=P₁^e1…P₁^et

dove P₁,…,P_t sono ideali primi distinti ed e₁,…,e_t sono interi positivi. Uno degli obiettivi principali della teoria algebrica dei numeri consiste nel fornire un procedimento che consenta di calcolare esplicitamente la fattorizzazione [17]. Tale procedimento è chiamato legge di reciprocità, poiché nel caso di un corpo quadratico ℚ(√d) è fornito dalla legge di reciprocità quadratica.

In generale è possibile mostrare che il numero di fattori t è al più pari al grado di F. Infatti, se il grado di F è n e se il gruppo quoziente O_F/p_i ha f_i elementi allora

[18] e₁f₁+e₂f₂+…+e_tf_t=n.

Nel caso che F sia un'estensione di Galois del corpo razionale

[19] e₁=e₂=…=e_t e f₁=f₂=…=f_t.

Teoria della ramificazione. Se qualche e_i è maggiore di 1, allora si dice che il primo p si ramifica in F. Esiste solo un numero finito di primi ramificati e questi sono precisamente i primi che dividono un certo intero Δ=Δ_F, chiamato il discriminante di F. Inoltre, se F è diverso da ℚ, allora qualche primo deve ramificarsi.

Le unità di O_F. Sia F=O_F(δ), dove δ è una radice dell'equazione polinomiale irriducibile f(x)=0. Supponiamo che f abbia r₁ radici reali e r₂ coppie di radici complesse. Allora le unità di O_F sono descritte dal risultato seguente.

Teorema sulle unità di Dirichlet-Minkowski. - Esistono una radice k-esima primitiva dell'unità ζ, s=r₁+r₂−1 e unità ε₁,…,ε_s tali che ogni unità ε di O_F può essere scritta in modo unico nella forma

[20] ε=ζ^rε₁^α1ε₂^α2…ε_p^αp

dove r,a₁,a₂,…,a_p sono interi e 0≤r〈k.

Il numero di classi. - Si dice che due ideali A e B appartengono alla stessa classe di ideali se esistono degli ideali principali (α) e (β) tali che (α)A=(β)B. Il numero di classi di ideali h_F è chiamato il numero di classi di F. Si dimostra che h_F è finito e che h_F=1 se e solo se O_F è un dominio a fattorizzazione unica.

Ci sono molti problemi aperti concernenti il numero di classi e altri di questo tipo sono stati risolti solo di recente.

Corpi quadratici. I più semplici corpi di numeri algebrici sono i corpi quadratici F=ℚ(√d). Se d>0 F è chiamato corpo quadratico reale, se d〈0 corpo quadratico immaginario. Nell'ultimo caso O_F ha soltanto un numero finito di unità, precisamente {±1} se d≠−1,−3, {±1,±i} se d=−1 e {±1,(±1±√−3)/2} se d=−3. Le unità di un corpo quadratico reale sono tutte della forma ±ε₀ⁿ, dove n è intero e ε₀ è la cosiddetta unità fondamentale. Se d≡2 o 3(mod 4), allora ε=x+y√d è un'unità di O_F se e solo se x²−dy²=±1. Così, essenzialmente, le unità sono determinate dalle soluzioni dell'equazione di Pell.

Sono state fatte numerose ricerche sul numero di classi dei corpi quadratici. Per esempio, già nelle sue Disquisitiones Gauss osservò che sembrava esserci solo un numero finito di corpi quadratici immaginari F aventi un fissato hF. Questo è vero e può essere dedotto dal teorema seguente.

Teorema di Siegel. Sia δ>0 fissato; allora esiste un numero positivo c=c(δ) tale che

[21] h_F>c(δ)∣d∣^1/2−δ F=ℚ(√d), d〈0.

Nessuno è ancora riuscito a determinare esplicitamente la costante c(δ) pertanto il risultato è di uso limitato nei calcoli. Gauss tentò di stilare un elenco esplicito dei corpi quadrici immaginari aventi numero di classi 1, ma il problema è stato risolto contemporaneamente nel 1966 da Alan Baker e Harold M. Stark. Essi dimostrarono che esistono esattamente nove corpi quadratici immaginari con numero di classi 1 e nel 1970 determinarono i corpi quadratici immaginari aventi numero di classi 2. Eppure, ancora oggi, si è ben lontani dal sapere come proseguire in questa direzione.

Le questioni riguardanti i numeri di classi dei corpi quadratici reali sono molto più oscure di quelle relative a quelli immaginari. Ancora Gauss suppose che esistono infiniti corpi quadratici reali aventi numero di classi 1, ma questa congettura appare inattaccabile con i metodi attuali. Ciononostante, il lavoro empirico di Sigekatu Kuroda, che si è servito di un calcolatore ad alta velocità, mostra come all'incirca l'80% dei primi due milioni di corpi quadratici reali hanno effettivamente numero di classi 1.

Una spiegazione completa delle connessioni tra la teoria degli ideali di un corpo quadratico e le forme quadratiche binarie è al di là degli scopi di questo articolo. Basterà dire che gli ideali appartenenti alla stessa classe sono associati a forme quadratiche binarie che possono essere trasformate l'una nell'altra con un cambiamento lineare di variabili avente determinante 1. Questa corrispondenza fornisce un dizionario col quale è possibile tradurre i problemi concernenti le forme quadratiche binarie in problemi di teoria degli ideali e viceversa.

Corpi ciclotomici. Benché lo studio iniziale dell'aritmetica dei corpi ciclotomici fosse stato motivato dall'interesse per l'ultimo teorema di Fermat, si è poi compreso che essi giocano un ruolo ben più intrinseco e fondamentale di quanto ci si sarebbe aspettati in un primo momento.

Il solo primo ramificato in F=ℚ(ζ), con ζ=cos(2π/p)++i sen(2π/p), è p e infatti pO_F=P^p−1. Una legge esplicita di decomposizione dei primi è data nel modo seguente: se f è il più piccolo intero positivo tale che q^f≡1(mod p), dove q è un primo non divisibile per p, allora

[22] qO_F=P₁…P_g, g=(p−1)/f.

In particolare, se q e q′ sono due primi tali che q≡≡q′(mod p) allora q e q′ si fattorizzano nello stesso modo in O_F. Così, come nel caso dei corpi quadratici, tutti i primi appartenenti alla stessa progressione aritmetica (in questo caso modulo p) si fattorizzano nello stesso modo.

I numeri di classi dei corpi ciclotomici sono stati considerati per la prima volta da Kummer nel suo lavoro sull'ultimo teorema di Fermat. Il suo argomento dimostra che x^p+y^p=z^p non ha soluzioni intere non nulle purché h_F non sia divisibile per p. Tali primi p sono chiamati regolari e Kummer congetturò che ne esistano infiniti. Tale asserzione manca ancora di una dimostrazione, ma è noto che esistono infiniti primi irregolari.

Sia ora F₀=ℚ(ζ+ζ⁻¹). Il numero di classi h₀ di F₀ divide h_F, sicché h₁=h_F/h₀ è un intero. I numeri h₁ e h₀ sono chiamati rispettivamente il primo fattore e il secondo fattore del numero di classi h_F. Un primo p è detto regolare se e solo se non divide h₀.

L'interpretazione del secondo fattore è meglio conosciuta di quella del primo: è noto per esempio che h₁ tende rapidamente all'infinito con p. Ne segue che esiste solo un numero finito di corpi ciclotomici aventi numero di classi assegnato. Un risultato di Hugh L. Montgomery e John M. Masley afferma che se p>19 risulta h₁>1.

Teoria del corpo di classi

Uno dei più significativi problemi non risolti della teoria algebrica dei numeri è quello di determinare una legge di reciprocità che descriva come un primo p si decompone in un arbitrario corpo di numeri algebrici F. In proposito, uno dei maggiori risultati in questo secolo è stato lo sviluppo della teoria del corpo di classi, che fornisce appunto una legge di reciprocità nel caso in cui F sia una estensione di Galois abeliana del corpo razionale ℚ.

Teoria del corpo di classi su ℚ. Le estensioni di Galois abeliane di ℚ sono descritte dal teorema di Kronecker-Weber: ogni estensione di Galois abeliana F di ℚ è contenuta in un corpo ciclotomico

[23] formula.

Se il più piccolo corpo ciclotomico contenente F è

[24] formula

allora γ è chiamato il conduttore di F. Di grande importanza è il seguente sviluppo.

Teorema 5. I primi che dividono il conduttore γ sono esattamente i primi che si ramificano in F.

Quanto alla fattorizzazione dei primi in F, supponiamo che p sia un primo non ramificato. Allora è possibile costruire un elemento [(F/ℚ)/p] del gruppo di Galois di F su ℚ con la seguente proprietà: se pO_F=P₁…P_g e f₁=…=f_g=f, allora [(F/ℚ)/p] ha ordine f. [(F/ℚ)/p] è chiamato simbolo di Artin (o automorfismo di Frobenius) e la conoscenza del suo ordine ci consente di stabilire come p si decompone in F. Nel caso particolare F=ℚ(√d), il simbolo di Artin [(F/ℚ)/p] si può identificare in modo naturale col simbolo di Legendre.

Il teorema fondamentale sul simbolo di Artin è la seguente lungimirante generalizzazione della legge di reciprocità quadratica.

Legge di reciprocità di Artin. Il simbolo di Artin dipende solo dalla progressione aritmetica modulo γ cui p appartiene. In altre parole, due primi che appartengono alla stessa progressione aritmetica modulo il conduttore si decompongono nello stesso modo in F.

Teoria del corpo di classi su un corpo arbitrario. Partendo da un arbitrario corpo di numeri algebrici F₀, è possibile costruire una descrizione esplicita delle sue estensioni di Galois abeliane. Esiste cioè una corrispondenza biunivoca tra certi sottogruppi del cosiddetto gruppo idele di F₀ e le estensioni di Galois abeliane. Inoltre esiste una corrispondenza naturale tra l'aritmetica di una estensione abeliana e le proprietà algebriche del sottogruppo corrispondente. In particolare è possibile descrivere il gruppo di Galois dell'estensione in termini del sottogruppo corrispondente in modo tale che, nel caso F₀=ℚ, il risultato è essenzialmente la legge di reciprocità di Artin descritta sopra.

Una recente conquista della teoria del corpo di classi è la soluzione negativa del problema di Hilbert sulla torre del corpo di classi da parte dei matematici russi Evgenij S. Golod e Igor R. Shafarevich nel 1964. Per gran parte del XX secolo si è sospettato che ogni corpo di numeri algebrici sia contenuto in un corpo di numeri algebrici avente numero di classi 1, ma a dispetto di considerevoli indicazioni nella direzione della tesi suddetta Golod e Shafarevich hanno fornito un procedimento generale per le costruzioni di controesempi. Uno di essi è

Un altro classico problema nella cui soluzione sono stati compiuti recenti progressi può essere formulato come segue. Sia G un gruppo finito assegnato: esiste un corpo di numeri algebrici F, estensione di Galois di ℚ, tale che il suo gruppo di Galois sia G? Se G è abeliano la risposta è positiva come è facile provare. Shafarevich, nel 1954, ha mostrato che la risposta è ugualmente affermativa nel caso in cui G sia un gruppo risolubile. Il problema nel caso generale resta tuttora aperto.

Teoria analitica dei numeri

Distribuzione dei primi

L'esistenza di infiniti primi era già nota agli antichi Greci e una corretta dimostrazione di questo fatto si trova negli Elementi di Euclide. - Tuttavia, la teoria moderna ha inizio con la dimostrazione di Eulero, che suggerisce una connessione tra le proprietà della distribuzione dei primi e il comportamento della funzione

[25] formula

per s∈ℂ. Questa osservazione è il punto di partenza della teoria analitica dei numeri. La serie che definisce ζ(s)converge assolutamente per tutti gli s complessi aventi parte reale maggiore di 1 ed è analitica per tali s. Si mostra che

[26] formula.

dove il prodotto è esteso a tutti i primi. La funzione ζ(s) è chiamata funzione zeta di Riemann e la rappresentazione [26] è chiamata rappresentazione tramite il prodotto euleriano.

Le proprietà analitiche di ζ(s), come le connessioni profonde con la teoria della distribuzione dei primi, furono esplorate dal matematico tedesco Bernhard Riemann nel 1859. Egli dimostrò che ζ(s) può essere prolungata analiticamente all'intero piano complesso come funzione meromorfa tale che ζ(s)−1/(s−1) è intera. Inoltre se R(s)=π^−s/2Γ(s/2)ζ(s) e Γ(s) indica la funzione gamma, allora R(s) ha poli solo per s=0,1 e

[27] R(s)=R(1−s).

L'espressione [27] è nota come l'equazione funzionale di ζ(s). Essa implica molte delle più profonde proprietà della funzione zeta.

Dalla rappresentazione mediante il prodotto euleriano segue che ζ(s)≠0 per Re(s)>1. È allora facile dedurre, facendo uso dell'equazione funzionale e partendo dal fatto che Γ(s) ha poli semplici per tutti gli interi negativi, che i soli zeri di ζ(s) per Re(s)〈0 sono s=−2,−4,−6,−8,…. Quindi tutti gli zeri diversi da questi si trovano nella cosiddetta striscia critica 0≤Re(s)≤1. A proposito di tali zeri non banali, Riemann formulò la seguente celebre congettura, nota appunto come ipotesi di Riemann: tutti gli zeri non banali di ζ(s) si trovano sulla linea Re(s)=1/2. Nonostante gli intensi sforzi da parte di un gran numero di ricercatori, questa rimane non dimostrata a più di un secolo dalla sua formulazione.

Due matematici francesi, Jacques Hadamard e Charles de la Vallée Poussin, hanno fornito indipendentemente nel 1896 la prima dimostrazione del teorema dei numeri primi. Essi lo hanno dedotto dal fatto che è possibile costruire piccole regioni nella striscia critica in cui ζ(s) non ha zeri e ancora per circa mezzo secolo le sole dimostrazioni note hanno continuato a basarsi su metodi di variabile complessa. Nel 1948 invece Atle Selberg e Paul Erdös ne hanno dato delle dimostrazioni elementari nel senso che non utilizzano la variabile complessa, ma assai complicate dal punto di vista tecnico.

Uno studio molto attento è stato dedicato alla distanza tra due primi consecutivi, cioè del tipo (p,p+2). L'evidenza numerica suggerisce l'esistenza d'infinite coppie, ma non è noto se questo sia vero o meno. Un risultato classico del tutto elementare, noto come postulato di Bertrand, asserisce che per ogni x≥1 esiste un primo tra x e 2x. Sono state condotte molte ricerche per migliorare questo teorema e attualmente il risultato migliore è dovuto a Montgomery: per ogni ε>0 esiste x₀=x₀(ε) tale che, per ogni x≥x₀, vi è un primo tra x e x+x^3/5+ε.

Primi nelle progressioni aritmetiche

Siano l e k interi. Affinché la progressione aritmetica

[28] l, l+k, l+2k,…

contenga infiniti primi è necessario che l e k siano primi tra loro, cioè che l e k non abbiano fattori comuni maggiori di 1. Indichiamo con l₁,…,l_t gli interi tra 0 e k primi con k. Allora tutti i primi eccetto un numero finito sono contenuti nelle t progressioni aritmetiche

[29] l_j, l_j+k, l_j+2k, … j=1,…,t.

Il numero t di tali progressioni è una funzione di k, indicata con φ(k) e chiamata funzione φ di Euler.

Lejeune Dirichlet ha mostrato per primo nel 1837 che ogni progressione [29] contiene infiniti primi e oggi per studiare la distribuzione dei primi in una progressione aritmetica s'introduce una serie di funzioni analitiche, chiamata serie L di Dirichlet, che generalizza la funzione zeta di Riemann.

La funzione zeta e la serie L sono legate all'aritmetica degli interi ℤ, ma esistono funzioni corrispondenti legate all'aritmetica dell'anello degli interi di un arbitrario corpo di numeri F. In particolare, l'analoga della funzione zeta di Riemann per F è chiamata funzione zeta di Dedekind ζ_F(s). Molte informazioni aritmetiche intorno a F possono essere ottenute da uno studio di ζ_F(s). Per esempio, se F è una estensione di Galois abeliana si può usare la legge di decomposizione dei primi in F per esprimere ζ_F(s) come prodotto di serie L di Dirichlet. Da questa rappresentazione derivano alcune conseguenze, fra cui una formula esplicita per il numero di classi h_F che ha originato molte interessanti ricerche.

Progressi nella direzione dell'ipotesi di Riemann

Indichiamo con T un numero positivo e con N(T) il numero di zeri ϱ=α+it della funzione zeta di Riemann, dove 0≤α≤1 e 0≤t≤T. Riemann congetturò che per qualche costante c indipendente da T

[30] formula

ovvero che ci sono all'incirca (1/2π)T log T zeri di ζ(s) nella striscia critica con ordinata compresa tra −T e T. Questo fatto è stato provato dal matematico tedesco Hans von Mangoldt nel 1901. Indichiamo ora con N₀(T) il numero di tali zeri che in più stanno sulla linea Re(s)=1/2. L'ipotesi di Riemann equivale ad asserire che N(T)=N₀(T). Pertanto sulla base di essa N₀(T) è asintoticamente (1/2π)T log T.

Grande è stato durante tutto il secolo scorso il lavoro per determinare l'esatto ordine di grandezza di N₀(T). Nel 1914 Godfrey H. Hardy ha mostrato che N₀(T) tende all'infinito quando T tende all'infinito. In altre parole, esistono infiniti zeri di ζ(s) sulla linea Re(s)=1/2. Nel 1921 lo stesso Hardy ha poi provato che N₀(T)>AT per una costante A indipendente da T. Questo risultato è stato migliorato in modo sostanziale da Selberg, che nel 1944 ha dimostrato che N₀(T)>AT log T. In altre parole, almeno una parte degli zeri di ζ(s) si trovano dove l'ipotesi di Riemann indica debbano essere. Nel 1974 Norman Levinson, migliorando il metodo di Selberg, ha dimostrato che

[31] formula.

Dunque, almeno un terzo degli zeri sono dove si suppone che siano. Sembra probabile che ulteriori miglioramenti nella determinazione della costante saranno compiuti in futuro.

Per mezzo di elaboratori elettronici ad alta velocità è stato compiuto un notevole lavoro di calcolo sugli zeri di ζ(s) e fino a oggi ne sono stati determinati oltre 67 milioni. Sono state inoltre verificate numerose conseguenze numeriche dell'ipotesi di Riemann e nessun risultato numerico ha dato luogo a fatti inconsistenti con essa, benché attualmente alcuni matematici dubitino della sua validità.

Uno dei motivi della sua importanza (per ζ(s) o una sua generalizzazione) è il fatto che molte affermazioni di natura aritmetica possono essere dimostrate, almeno fino a oggi, soltanto facendone uso.

In anni recenti ci sono stati molti tentativi tesi a dimostrare delle forme approssimative o di media dell'ipotesi di Riemann. Tali risultati derivano in genere da disuguaglianze che forniscono stime importanti per i polinomi trigonometrici, note con il nome collettivo di crivello largo introdotto dal teorico dei numeri russo Yuri V. Linnik. Tipici risultati dicono che la maggior parte degli zeri di ζ(s) (o della serie L) si trovano vicini alla linea Re(s)=1/2. Enrico Bombieri e A.I. Vinogradov hanno usato il crivello largo per dimostrare che, almeno in media, il teorema dei numeri primi per le progressioni aritmetiche vale con un termine di errore che è quello che discende dall'ipotesi di Riemann.

La teoria dei numeri irrazionali

Origini della teoria

Un numero irrazionale è un numero che non è razionale, cioè che non è della forma p/q, con p,q interi e q≠0. Esempi di numeri irrazionali sono:

[32] formula.

I primi tre esempi sono numeri algebrici; π ed e, invece, non lo sono. In altre parole π ed e non sono radici di nessuna equazione algebrica a coefficienti razionali. Numeri siffatti sono chiamati trascendenti.

Un ramo della teoria dei numeri si occupa dello studio delle proprietà dei numeri irrazionali. Tra i principali problemi considerati figurano: (a) quali numeri irrazionali siano trascendenti e quali algebrici; (b) fino a che punto si possano approssimare i numeri irrazionali con i razionali. Risulta che tali questioni hanno uno stretto legame con l'aritmetica degli interi e dei corpi di numeri algebrici.

Numeri trascendenti

Un numero irrazionale può essere bene approssimato dai razionali come mostra il seguente risultato.

Teorema di Dirichlet. Sia α un numero irrazionale. Allora esiste una successione infinita di numeri razionali p/q, q>0 tale che

[33] formula.

Al contrario i numeri algebrici non possono essere approssimati troppo bene.

Teorema di Liouville. Sia α un numero algebrico di grado n. Allora esiste una costante c, dipendente da α, tale che per ogni numero razionale p/q, q>0, risulta

[34] formula.

Quindi se un numero irrazionale è approssimabile troppo bene mediante i razionali, allora è necessariamente trascendente. Liouville usò questa idea nel 1844 per dare i primi esempi di numeri trascendenti. Un esempio tipico è

[35] formula

dove n!=1∙2…n.

Il matematico tedesco Georg Cantor dimostrò che i numeri algebrici formano un insieme numerabile, cioè che possono essere messi in corrispondenza biunivoca con gli interi. Egli dimostrò anche che i reali e i complessi, al contrario, non sono numerabili. Quindi, la maggior parte dei numeri reali è trascendente. Tuttavia per decidere se un dato numero è o no trascendente è necessario ricorrere ad argomenti tortuosi e complicati.

Charles Hermite nel 1873 dimostrò la trascendenza di e, segnando così l'inizio della moderna teoria dei numeri trascendenti. La trascendenza di π è più complicata ed è stata provata per la prima volta da Ferdinand von Lindemann nel 1882, generalizzando i metodi di Hermite. Lindemann in realtà andò più in là, dimostrò un teorema generale da cui segue la trascendenza di e, di π e di molti altri numeri.

Nel 1900 il matematico tedesco David Hilbert, parlando al Congresso internazionale dei matematici, pose una serie di 23 problemi destinati ai ricercatori del XX secolo.

Il settimo era di determinare se 2^√2 è trascendente. In meno di 30 anni si è data a esso una risposta affermativa: il fatto che 2^√2 è trascendente segue dal teorema di Gel'fond-Schneider, dimostrato dai due indipendentemente nel 1934.

Teorema 6. Siano α e β numeri algebrici, α≠0,1, β irrazionale. Allora α^β è trascendente.

Per quanto attualmente si sappiano molte cose sui numeri trascendenti, anche questioni formulate in modo semplice sembrano sfidare l'eventuale soluzione. È noto che e^π è trascendente, ma il problema riguardante π^e è ancora aperto.

Al decimo posto nella lista di Hilbert c'è il problema di fornire un algoritmo per determinare, con un numero finito di calcoli, se una certa equazione diofantea ha soluzione. Nel 1970 Jurij Matijaševič, basandosi sul lavoro di Julia Robinson, Hilary Putnam e Martin Davis, ha dimostrato che un tale algoritmo non esiste. La soluzione del decimo problema di Hilbert si fonda sostanzialmente su metodi di logica matematica.

La teoria delle funzioni automorfe

La teoria della distribuzione dei primi non è la sola relazione tra teoria dei numeri e funzioni di una variabile complessa. Un'altra profonda connessione esiste per tramite della teoria delle funzioni automorfe. Queste funzioni, introdotte per la prima volta da Gauss e Carl G. Jacobi, implicano molti fatti di natura aritmetica, principalmente intorno alle equazioni diofantee e alla teoria del corpo di classi.

Forme automorfe

Indichiamo con Γ il gruppo delle matrici 2×2 con elementi interi e determinante 1. Γ è chiamato gruppo modulare ellittico. Indichiamo con ℍ il semipiano superiore complesso, cioè l'insieme di tutti i numeri complessi x+iy, con x,y reali e y>0. Se

[36] formula

è in Γ, γ può agire su ℍ nel modo seguente:

[37] formula.

Una forma automorfa di peso k per Γ è una funzione f(z) definita per z in ℍ tale che:

a b

a) f(γ(z))(cz+d)^−k=f(z), γ=()

c d

b) f(z) è olomorfa in ℍ;

c) f(z) ha uno sviluppo di Fourier del tipo

[38] formula.

Le forme automorfe compaiono in modo naturale nella teoria delle funzioni ellittiche.

Un importante esempio (di peso 12 per Γ) è dato dalla funzione Δ di Dedekind:

[39] formula.

Molte delle applicazioni della teoria delle funzioni automorfe alla teoria dei numeri discendono da due principî basilari. Il primo di essi è che i coefficienti di Fourier di forme automorfe sono spesso quantità interessanti dal punto di vista aritmetico.

Sono state fatte molte ricerche sulla natura dei coefficienti dello sviluppo di Fourier di forme automorfe. Hardy, John E. Littlewood e Srinivasa Ramanujan hanno introdotto il metodo del cerchio, che è una tecnica per approssimare tali coefficienti.

Scriviamo per esempio lo sviluppo di Fourier di Δ(z):

[40] formula.

τ(n) è chiamata funzione τ di Ramanujan e ha molte interessanti e profonde proprietà aritmetiche.

Il secondo principio basilare è che le forme automorfe di peso k formano uno spazio vettoriale complesso di dimensione finita. Quindi, se si è in grado di trovare esplicitamente una base di questo spazio vettoriale sarà possibile, esprimendo una forma automorfa f in termini di essa, calcolare i coefficienti di Fourier di f a partire dai coefficienti di Fourier delle forme della base.

Prendendo spunto dall'evidenza numerica, Ramanujan congetturò che per ogni ε>0 esista una costante C=C(ε) tale che

[41] formula.

In particolare egli suppose che per i primi p si abbia

[42] ∣τ(p)∣〈2p^11/2.

Questa congettura è molto profonda ed è stata dimostrata solo di recente da Pierre Deligne, nel 1974.

Moltiplicazione complessa

Il teorema di Kronecker-Weber asserisce che ogni estensione di Galois abeliana di ℚ è contenuta in un corpo ciclotomico ℚ(ζ), ζ=e^2πi/n. In altre parole ogni estensione di Galois abeliana può essere scritta come ℚ(α), dove α è uno speciale valore della funzione esponenziale. Leopold Kronecker, verso la metà del XIX sec., congetturò che particolari valori di funzioni automorfe possano dar luogo a estensioni abeliane di corpi quadratici immaginari. Quest'idea è stata sviluppata verso la fine del secolo scorso da Heinrich Weber e Karl R. Fueter e più tardi da Helmut Hasse e Max Deuring, dando luogo alla teoria della moltiplicazione complessa.

Una funzione automorfa per Γ è una funzione meromorfa f(z) su ℍ tale che

[43] f(γ(z))=f(z) γ ∈ Γ

e inoltre con uno sviluppo di Fourier della forma

[44] formula

dove N può essere eventualmente negativo.

Sia K un corpo quadratico immaginario, P un ideale primo di O_K. Se L è un'estensione di Galois di K allora PO_L, il più piccolo ideale di O_L contenente P, può essere scritto come prodotto di potenze di ideali primi di O_L:

[45] PO_L=pⁱ_e…p^e_t.

Se e>1, P si dice ramificato nell'estensione L/K. In generale, t è minore o uguale del grado di L/K e in questo secondo caso si dice che P si spezza completamente in L/K. Sia ℱ un ideale di O_K, L un'estensione di Galois di K. Si dice che L è il corpo di classi radiale (ray class field) mod ℱ di K, indicato con K_ℱ, se gli ideali primi P che si spezzano completamente in L/K sono esattamente quelli della forma P=αO_K, con α−1 in ℱ. Dalla teoria del corpo di classi segue che esiste uno e un solo corpo di classi radiale modulo ℱ. Inoltre, se K_N indica il corpo di classi radiale per ℱ=N=O_K con N intero positivo, allora ogni estensione abeliana di K è contenuta in K_N per qualche N. Quindi il corpo di classi radiale generalizza le estensioni ciclotomiche di ℚ. La teoria della moltiplicazione complessa indica come costruire K a partire da speciali valori di funzioni automorfe.

Il corpo di classi radiale K_ℱ può essere caratterizzato come la massima estensione abeliana di K in cui si ramificano solo i primi che dividono ℱ. In particolare, se ℱ=O_K allora K_ℱ è la massima estensione abeliana di K in cui nessun primo è ramificato. Questo particolare corpo di classi radiale è chiamato corpo di classi di Hilbert di K ed è indicato con K_hil.

Se A è un ideale di O_K, esistono w₁,w₂ in O_K tali che A consiste di tutti i numeri della forma xw₁+yw₂, con x,y in ℤ. In questo caso si scrive A=[w₁,w₂]. Invertendo l'ordine di w₁ e w₂, se necessario, è sempre possibile supporre che w₁/w₂ appartenga a ℍ.

Teorema fondamentale della moltiplicazione complessa. Siano K un corpo quadratico immaginario, A=[w₁,w₂] un ideale di O_K, N un intero positivo:

a) K_hil=K(j(w₂/w₁));

b) K_N=K(j(w₂/w₁), f^N_1,0(w₂/w₁), f^N_2,0(w₂/w₁), …,

f^N_N−1,N−1(w₂/w₁))

dove f_a,b è la cosiddetta funzione di Weber.

Col suo dodicesimo problema Hilbert invitò i matematici a formulare una generalizzazione della teoria della moltiplicazione complessa che consentisse la costruzione di estensioni abeliane di ogni corpo di numeri K usando speciali valori di funzioni analitiche. Un primo tentativo di formulare una tale teoria è stato fatto da Erich Hecke nel 1912, il quale si è occupato del caso in cui K è un corpo quadratico reale. In anni recenti si sono compiuti molti progressi su questa questione, dovuti principalmente a Goro Shimura, il cui lavoro collega il problema della costruzione del corpo di classi con la teoria delle varietà abeliane di dimensione più alta.

Il lavoro di Hecke

Il padre della teoria aritmetica moderna delle funzioni automorfe è Hecke, le cui ricerche costituiscono la base per gran parte del lavoro attuale sull'argomento.

La sua teoria mostra che almeno in una certa misura funzioni zeta e forme automorfe sono come i due lati di uno stesso angolo: esaminando le corrispondenti funzioni zeta è possibile stabilire dei risultati riguardanti le forme automorfe e viceversa.

Indichiamo con ℳ_k(Γ) lo spazio delle forme automorfe di peso intero k per il gruppo modulare ellittico Γ. Le funzioni zeta corrispondenti a queste forme automorfe hanno tutte prolungamenti analitici ed equazioni funzionali. Hecke ha determinato quali di queste funzioni zeta si rappresentano mediante il prodotto euleriano e ha definito sullo spazio vettoriale ℳ_k(Γ) una famiglia di operatori lineari T_n, con n≥1, ora chiamati operatori di Hecke. Questi formano un anello commutativo e possono essere diagonalizzati simultaneamente, sicché ℳ_k(Γ) è generato da forme che sono simultaneamente autofunzioni di tutti gli operatori di Hecke. Se una di tali autofunzioni è data da

[46] formula

allora f(z) può essere normalizzata in modo tale che a₁=1. Le funzioni zeta corrispondenti alle autofunzioni degli operatori di Hecke così normalizzate sono precisamente quelle che si rappresentano mediante il prodotto euleriano. Se la funzione zeta corrispondente a f(z) è

[47] formula

la sua rappresentazione mediante il prodotto euleriano si scrive

[48] formula

dove il prodotto è esteso a tutti i primi p.

Un esempio interessante di questa teoria è dato da

[49] formula.

La corrispondente funzione zeta è

[50] formula.

Questa può essere prolungata analiticamente a una funzione intera di s e soddisfa l'equazione funzionale

[51] R(s)=R(12−s), R(s)=(2π)^−sΓ(s)φ(s).

Inoltre φ(s) ha un prodotto euleriano

[52] formula.

Risulta che il coefficiente di Fourier a_p di una autofunzione degli operatori di Hecke opportunamente normalizzata è un autovalore di T_p. La congettura di Ramanujan sulla grandezza di τ(p) può quindi essere generalizzata nel modo seguente.

Congettura di Hecke-Ramanujan-Peterson. Sia λ_p un autovalore di T_p su ℳ_k(Γ), allora

[53] ∣λ_p∣〈2p^(k−1)/2.

Questa congettura è connessa al lavoro di Deligne citato sopra. Una delle più significative tendenze nella teoria dei numeri degli ultimi cento anni è infatti l'uso sempre maggiore del linguaggio e degli strumenti della geometria algebrica nei problemi aritmetici.

Bibliografia

Adams, Goldstein 1975: Adams, William - Goldstein, Larry, An introduction to number theory, Englewood Cliffs (N. J.), Prentice-Hall, 1975.

Artin 1965: Artin, Emil, The collected papers of Emil Artin, edited by Serge Lang, John Tate, Reading (Mass.), Addison-Wesley, 1965.

Baker 1975: Baker, Alan, Transcendental number theory, London, Cambridge University Press, 1975.

Borevich, Shafarevich 1966: Borevich, Zenon I. - Shafarevich, Igor, Number theory, New York, Academic Press, 1966.

Cassels 1957: Cassels, John W.S., An introduction to diophantine approximation, Cambridge, Cambridge University Press, 1957.

Cassels 1966: Cassels, John W.S., Diophantine equations with special reference to elliptic curves, "Journal of the London Mathematical Society", 2, 1966, pp. 193-291.

Cassels, Fröhlich 1967: Algebraic number theory, edited by John W.S. Cassels, Albrecht Fröhlich, London, Academic Press, 1967.

Davenport 1967: Davenport, Harold, Multiplicative number theory, Chicago, Markham, 1967.

Davis 1973: Davis, Martin, Hilbert's tenth problem is unsolvable, "American mathematical monthly", 80, 1973, pp. 233-269.

Dickson 1967: Dickson, Leonard E., Algebraic numbers, New York, Chelsea, 1967.

Estermann 1961: Estermann, Theodor, Introduction to modern prime number theory, Cambridge, Cambridge University Press, 1961.

Gel'fond 1960: Gel'fond, Aleksandr O., Transcendental and algebraic numbers, New York-London, Dover, 1960.

Goldstein 1971: Goldstein, Larry J., Analytic number theory, Englewood Cliffs (N.J.), Prentice-Hall, 1971.

Goldstein 1971: Goldstein, Larry J., A history of the prime number theorem, "American mathematical monthly", 80, 1973, pp. 599-614.

Grosswald 1966: Grosswald, Emil, Topics from the theory of numbers, New York, Macmillan, 1966.

Gunning 1962: Gunning, Robert C., Lectures on modular forms, Princeton, Princeton University Press, 1962.

Hardy, Wright 1960: Hardy, Godfrey H. - Wright, Edward M., The theory of numbers, Oxford 1960.

Hasse 1965: Hasse, Helmut, Zahlbericht, Wien, Physica, 1965.

Hecke 1959: Hecke, Erich, Mathematische Werke, Göttingen, Vandenhoek & Ruprecht, 1959.

Ireland, Rosen 1972: Ireland, Kenneth - Rosen, Michael, Elements of number theory, Tarrytown-on-Hudson (N.Y.), Bogden Quigley, 1972.

Kline 1972: Kline, M., Mathematical thought from ancient to modern times, New York, Oxford University Press,1972.

Knopp 1970: Knopp, Martin I., Modular functions in analytic number theory, Chicago, 1970.

Landau 1909: Landau, Edmund G.H., Handbuch der Lehre von der Verteilung der Primzahlen, Leipzig-Berlin, Teubner, 1909, 2 v.

Landau 1927: Landau, Edmund G.H., Vorlesungen über Zahlentheorie, Leipzig, Hirzel, 1927, 3 v.

Landau 1949: Landau, Edmund G.H., Einführung in die elementare und analytische Theorie der algebraischen Zahlen und der Ideale, 2. ed., New York, Chelsea, 1949.

Lang 1966: Lang, Serge, Introduction to transcendental numbers, Reading (Mass.), Addison-Wesley, 1966.

Lang 1970: Lang, Serge, Algebraic number theory, Reading (Mass.), Addison-Wesley, 1970.

Lang 1974: Lang, Serge, Elliptic functions, Reading (Mass.), Addison-Wesley, 1974.

Le Veque 1956: Le Veque, William, Topics in number theory, Reading (Mass.), Addison-Wesley, 1956, 2 v.

Montgomery 1971: Montgomery, Hugh, Topics in multiplicative number theory, Berlin-New York, Springer, 1971.

Mordell 1969: Mordell, Louis J., Diophantine equations, New York, 1969.

Niven 1967: Niven, Ivan, Irrational numbers, 3 ed., New York, Wiley, 1967.

Ogg 1969: Ogg, Andrew, Modular forms and Dirichlet series, New York, Benjamin, 1969.

Pollard 1950: Pollard, Harry, The theory of algebraic numbers, New York, Wiley, 1950.

Rademacher 1973: Rademacher, Hans, Topics in analytic number theory, Berlin, Springer, 1973.

Robert 1973: Robert, Andrew, Elliptic curves, Berlin, Springer, 1973.

Schilling 1965: Arithmetical algebraic geometry, edited by Otto F.G. Schilling, New York, Harper and Ross, 1965.

Schneider 1957: Schneider, Theodor, Einführung in die transzendenten Zahlen, Berlin, Springer, 1957.

Serre 1973: Serre, Jean-Pierre, A course in arithmetic, New York, Springer, 1973.

Shimura 1968: Shimura, Goro, Automorphic functions and number theory, Berlin, Springer, 1968.

Shimura 1971: Shimura, Goro, Introduction to the arithmetic theory of automorphic functions, Princeton, Princeton University Press, 1971.

Shimura 1961: Shimura, Goro - Tanujaina, Yutaka, Complex multiplication of abelian varieties and its applications to number theory, Tokyo, Mathematical Society of Japan, 1961.

Siegel 1969: Siegel, Carl L., Topics in complex function theory, New York, Wiley, 1969.

Swinnerton-Dyer 1967: Swinnerton-Dyer, H. Peter F., On the conjectures of Birch, Swinnerton-Dyer, and of Tate, in: Proceedings of a conference on local fields, Berlin, Springer, 1967, pp. 132-157.

Swinnerton-Dyer 1969: Swinnerton-Dyer, H. Peter F., Applications of algebraic geometry to number theory, in: 1969 Number Theory Institute, Providence (R.I.), American Mathematical Society, 1971, pp. 1-52.

Titchmarsh 1951: Titchmarsh, Edward C., The theory of the Riemann zeta-function, Oxford, Clarendon, 1951.

Weil 1948: Weil, André, Sur les courbes algébriques et les variétés qui s'en déduisent, Paris, Hermann, 1948.

Weil 1967: Weil, André, Basic number theory, Berlin, Springer, 1967.