Giochi, teoria dei

Giochi, teoria dei

1. Introduzione e cenni storici

La teoria dei giochi venne presentata per la prima volta, con questo nome e in modo sufficientemente organico, nel celebre trattato del matematico John von Neumann e dell'economista Oskar Morgenstern dal titolo Theory of games and economic behavior del 1944, ma è l'edizione del 1947, rivista e completata con la teoria dell'utilità, quella cui si fa comunemente riferimento; su importanti precursori si darà qualche cenno fra breve. Da allora il nome di questa teoria si è talmente consolidato che sarebbe impensabile cambiarlo; tuttavia si deve riconoscere che la denominazione non è tra le più felici e che, per chi non conosca almeno vagamente il contenuto della teoria, può riuscire fuorviante.

Un buon esempio di denominazione più descrittiva dei contenuti (ma non è una proposta di cambiamento di nome) è interactive decision theory (v. Aumann, 1987, p. 460). Comunque ancora oggi si continua a chiamare gioco una qualunque situazione competitiva, giocatori i contendenti (anche se sono delle società petrolifere o dei generali) e così via. A questo punto si impone, ovviamente, una prima, sommaria esposizione dell'oggetto della teoria.

Nei più svariati campi dell'attività umana si presentano situazioni in cui due o più individui (intendendo tale parola in senso lato) si trovano in competizione tra loro: ovvi gli esempi in campo economico (concorrenza commerciale), bellico, ecc. Con una generalizzazione alquanto discutibile si può anche pensare che uno dei competitori, invece di essere un individuo sia la 'natura': questo caso sarà considerato a parte (v. § 2h). Si comprende come i classici giochi da tavolo - scacchi, dama, giochi di carte - si presentino naturalmente quali comode schematizzazioni di situazioni competitive: da ciò il nome della teoria. Quanto allo scopo, esprimendoci per ora in modo grossolano, essa si propone di indicare, per ciascun 'giocatore', il modo migliore di comportarsi per ottenere il risultato migliore. Già questa frase vaga mette in luce che la teoria dei giochi ha natura normativa, ove se ne accettino le premesse, e non descrittiva.

Tra i menzionati precursori deve essere ricordato Émile Borel che negli anni venti, in vari articoli, pose le basi della teoria dei giochi limitatamente al caso di due giocatori e senza giungere alla dimostrazione del teorema del minimax, che anzi egli non credeva valido in generale, pur avendolo dimostrato in casi particolari (v. Borel, 1921 e i contributi del 1953). Come curiosità storica va infine menzionato un certo monsieur de Waldegrave che sin dal 1712, sia pure solo nel caso di un particolare gioco di carte, era pervenuto a quella 'soluzione' che costituisce il principale risultato della moderna teoria dei giochi. Questa 'soluzione', citata nel postscriptum di una lettera di R. de Montmort a N. Bernoulli, fu ignorata o trascurata sino al 1959, quando la mise in luce G. Th. Guilbaud (per più ampie notizie, v. De Finetti, 1969). È interessante il fatto che R.A. Fisher, avendo conosciuto il problema, ma non la soluzione, fornì la stessa soluzione nel 1934, senza però trarne conseguenze generali.

2. Giochi tra due persone a somma nulla

Definizione e forma estensiva

La precisazione 'a somma nulla' significa che la somma (algebrica) degli importi guadagnati alla fine dai due giocatori è zero; in altre parole, ciò che uno vince l'altro perde e viceversa. Con maggiore aderenza alla realtà, ci si dovrebbe occupare dell'utilità degli importi o, generalizzando, dell'utilità di una posta qualsiasi (guadagno o perdita di tempo, di prestigio, ecc.), ma ciò comporterebbe complicazioni (in particolare per la condizione a somma nulla) che all'inizio è opportuno evitare. Nel gioco possono intervenire, oppure no, elementi aleatori. Tipici esempi di giochi in cui non intervengono elementi aleatori sono gli scacchi, la dama, ecc. Ovvi e numerosissimi gli esempi del caso opposto.

Un gioco tra due persone è definito da una regola che stabilisce a chi tocca la prima mossa, se al giocatore 'I', o al giocatore 'II', o al 'caso'. Se si tratta di una mossa personale, la regola stabilisce le possibili alternative (che si suppongono in numero finito); se la mossa è lasciata al caso (come il risultato del lancio del dado), non solo la regola fissa le possibili alternative (sempre in numero finito), ma ne specifica le probabilità. Per la k-esima mossa (k>1), la regola del gioco, in base alle precedenti k-1 mosse: a) stabilisce se è una mossa del caso o di uno dei due giocatori; b) se è una mossa del caso, elenca le possibili alternative e specifica le singole probabilità; c) se è una mossa personale, stabilisce a quale giocatore tocca, elenca le sue possibili alternative e precisa quali sono le informazioni del giocatore sulle precedenti scelte e sui precedenti risultati prima che egli faccia la sua scelta.

Naturalmente la regola precisa quand'è che il gioco si deve ritenere terminato, nonché il risultato; infine si suppone che essa sia tale che il gioco termini dopo un numero finito di mosse.

A causa delle ipotesi fatte i giochi del tipo appena definito si sarebbero dovuti chiamare 'giochi finiti tra due persone, a somma nulla', ma, per brevità, si usa sottintendere tale precisazione. Diventa naturalmente obbligatorio dare la precisazione 'infiniti' (o altra equivalente) se manca l'ipotesi contraria sul numero delle scelte o sulla durata del gioco.

Un'ipotesi importante è che ognuno dei giocatori sia perfettamente a conoscenza della regola del gioco e delle funzioni di utilità di ciascun giocatore. Un gioco in cui siano rispettate queste condizioni dicesi a informazione completa, ed è sotto questa ipotesi - salvo avviso in contrario - che si sviluppa la teoria dei giochi qui riportata. Tuttavia il fatto che nella realtà spesso le condizioni indicate non siano verificate ha portato allo sviluppo di teorie basate sull'ipotesi di informazione incompleta (v., per esempio, Harsanyi e Selten, 1972), in cui assume particolare importanza l'impostazione bayesiana del calcolo delle probabilità.

La forma estensiva in cui si può porre un gioco, introdotta da von Neumann nel 1928 (v. von Neumann, 1928), si ottiene indicando, mossa dopo mossa, tutto ciò che è essenziale (stato d'informazione, alternative possibili, ecc.) a ogni momento del gioco, e naturalmente il risultato (payoff) al termine del gioco, per ogni singolo modo in cui il gioco può finire.

fig. 1

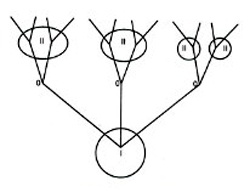
Una comoda rappresentazione grafica è riportata nella fig. 1 (albero del gioco). Ivi ogni vertice segnato con I, II, 0, indica una mossa del giocatore I, o del II, o del caso; le alternative possibili non sono altro che i rami che si dipartono da quel vertice; i raggruppamenti di vertici di tipo I o II indicano lo stato d'informazione del giocatore che deve muovere. Se un giocatore si trova in un vertice appartenente a un insieme di n vertici, egli sa solo di trovarsi in uno di quegli n vertici (con una certa distribuzione di probabilità), ma non in quale. Nel caso n=1 egli sa con certezza quale sia la sua posizione. Per questi insiemi di vertici (detti 'insiemi d'informazione') devono essere verificate delle ovvie proprietà: a) ogni vertice appartenente a uno stesso insieme deve competere allo stesso giocatore e avere lo stesso numero di alternative; b) se è possibile passare da un certo vertice a un altro, questi non possono appartenere allo stesso insieme d'informazione.

Nei vertici terminali dell'albero (i possibili modi in cui finisce il gioco) è indicato il risultato (positivo o negativo) per il giocatore I; ovviamente gli stessi valori col segno cambiato costituiscono il risultato per il giocatore II.

L'importanza di questa forma del gioco (e ciò vale in genere anche per le altre) è molto più di natura concettuale che pratica; si pensi, con riferimento solo alle primissime mosse, a come si presenterebbe l'albero del gioco degli scacchi.

La forma estensiva di un gioco ha avuto notevole importanza nello sviluppo della teoria, anche in casi più generali di quello 'tra due persone, a somma nulla'.

Forma normale

La denominazione 'forma normale' è oggi per lo più sostituita da altre, come 'forma matriciale' (un tempo 'forma rettangolare'), oppure 'forma strategica': qui conserviamo la prima denominazione anche per motivi storici. Per comprendere come si pervenga a questa forma valgono le seguenti considerazioni.

Generalmente un giocatore prende le sue decisioni man mano che si presenta la necessità di prenderle; in altre parole, con riferimento allo schema precedente, attende di trovarsi effettivamente in un vertice dell'albero, o meglio in un insieme d'informazione, in cui tocca a lui prendere una decisione per fare la sua scelta. È però evidente che egli potrebbe senz'altro stabilire quale decisione prenderebbe se si trovasse in quella situazione, ancor prima di cominciare il gioco: ai fini di una decisione razionale non vi è alcuna differenza, ove si prescinda da elementi estranei (come lo stato emotivo, per esempio), tra trovarsi effettivamente in una certa situazione e supporre di trovarcisi. Questa semplice osservazione consente quella notevole e semplicissima schematizzazione d'un gioco che costituisce la riduzione in 'forma normale'. Si supponga invero che la scelta predetta sia fatta a priori, per ogni possibile situazione, da parte di entrambi i giocatori: si dice allora che ognuno di essi ha scelto una particolare strategia. Dopo di ciò, se il gioco è privo di fattori aleatori, il suo risultato è perfettamente determinato, senza alcun bisogno di giocare effettivamente. Dichiarate, cioè, le rispettive strategie di I e II (che si suppongono scelte indipendentemente e all'insaputa dell'avversario), è precisato quanto ciascuno vince (o perde). Se invece entrano in gioco fattori aleatori, risulterà precisato il valore medio del guadagno di ciascun giocatore.

Se il giocatore I ha a disposizione m strategie e l'altro n, ogni possibile andamento del gioco sarà rappresentato da una matrice di m righe ed n colonne; se I sceglie la sua strategia r-esima e II la sua strategia s-esima, il risultato del gioco è fornito dall'elemento ars. Basta una matrice sola perché il gioco è a somma nulla (altrimenti ne occorrerebbero due): con la convenzione che gli ars rappresentino guadagni del giocatore I (positivi o negativi), gli stessi col segno cambiato rappresentano quelli del II, o più semplicemente, senza cambiar segno, rappresentano le perdite (positive o negative) del II.

Con riferimento alla forma matriciale del gioco, il termine riga si può considerare come sinonimo di 'strategia pura del giocatore II'. Il motivo della precisazione 'strategia pura' sarà chiarito in seguito (v. § 2f).

Strategie pure, minimax

matrice 2

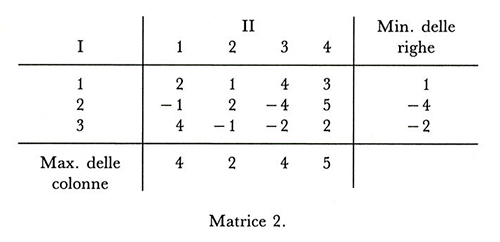
Per comprendere l'essenza del problema che si presenta, è opportuno servirsi di un esempio numerico (v. matrice 2). Se il giocatore I conoscesse la strategia scelta da II (cioè la colonna corrispondente nella matrice), avrebbe interesse a scegliere quella sua strategia che, su quella data colonna, gli fornisce il guadagno massimo; per esempio, se II scegliesse la strategia 3, I sceglierebbe la 1, perché il massimo valore della colonna 3 si ha sulla riga 1 (ed è precisamente 4). Analogo ragionamento se II conoscesse la strategia scelta da I, tenendo però conto che gli elementi della matrice sono guadagni di I e perdite di II: quest'ultimo avrebbe interesse a scegliere la colonna che su quella data riga gli fornisce il minimo (del guadagno di I, cioè della propria perdita). Per esempio, se I scegliesse la strategia 2, e II ne fosse informato, quest'ultimo sceglierebbe la strategia 3, perché il minimo della riga 2 si ha nella colonna 3 (e vale -4). Si pone il problema di stabilire un criterio di scelta nel caso, che è quello effettivo, in cui ciascun giocatore ignora la decisione dell'altro.

Un criterio (di cui però si vede subito la labilità, in generale) potrebbe essere il seguente. Il giocatore I considera i minimi di ciascuna riga, cioè il minimo guadagno assicuratogli da ogni singola strategia, e di questi minimi cerca il massimo; la corrispondente strategia, che può essere chiamata 'strategia maximin' gode di questa proprietà: gli garantisce un guadagno minimo superiore al guadagno minimo che otterrebbe con ogni altra strategia. Analogamente II, se usasse lo stesso criterio, dovrebbe determinare i massimi delle singole colonne e scegliere la strategia ('strategia minimax') che corrisponde al minimo di questi massimi. Alcuni autori chiamano maxmin il primo dei due valori e minmax il secondo. L'origine di tali nomi è ovvia:

maxmin = max_h min_k a_hk

minmax = min_k max_h a_hk

matrice 1

(con a_hk si indica l'elemento generico della matrice 1).

Si dimostra immediatamente che, per ogni matrice,

maxmin ≤ minmax.  (1)

Per esempio, nel caso numerico della matrice 2, vale la (1) con il segno <: infatti 1<2.

Il criterio prudenziale di gioco, illustrato tramite la matrice 2, non è in generale soddisfacente per i seguenti motivi. I, se sospetta che II segua il criterio accennato, e cioè che decida di scegliere la colonna 2, riterrà più conveniente scegliere, invece della riga 1 (che sarebbe suggerita dal medesimo criterio), la riga 2, che gli assicura un guadagno 2 in luogo di 1. II, a sua volta, potrebbe pensare che I abbia pensato questo, e in tal caso sarebbe portato a preferire la colonna 3, che, sulla riga 2, gli procura un guadagno 4 invece di una perdita 2. Si vede subito che, nell'esempio scelto, questo meccanismo dell"io penso ch'egli pensi che io pensi, ecc.' non porta ad alcun punto d'equilibrio e toglie consistenza al criterio iniziale. Ciò avviene perché per il gioco espresso dalla matrice 2 la (1) sussiste col segno <.

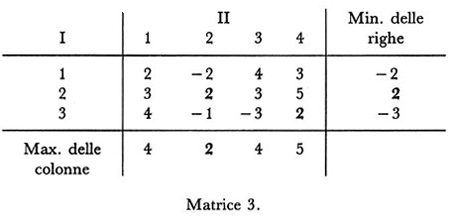
Consideriamo infatti un gioco in cui la (1) sussista col segno =, per esempio quello espresso dalla

In questo caso risulta

maxmin = minmax = 2.

fig. 2

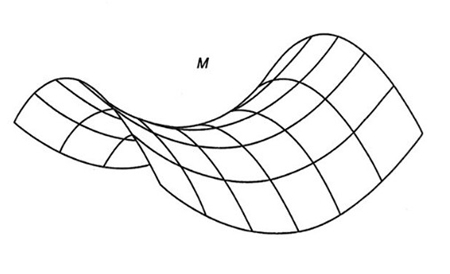
Se ora I sospetta che II scelga la colonna 2, ciò non lo porta affatto a cambiare la riga scelta, se aveva scelto la riga 2, perché in ogni altro caso guadagnerebbe di meno. Analogo ragionamento vale per II.Questo fatto avviene tutte le volte che la matrice possiede un elemento che sia simultaneamente il minimo della propria riga e il massimo della propria colonna; a un punto siffatto viene dato il nome di punto di sella, con riferimento al noto caso geometrico di una superficie in cui esistono due curve-sezione che si incontrano in un punto M che è il massimo di una e il minimo dell'altra (v. fig. 2).

Se ars è l'elemento della matrice che costituisce il punto di sella, le due strategie r-esima (per il giocatore I) ed s-esima (per il II) si dicono in equilibrio per i motivi già visti a proposito dell'esempio numerico; formalmente la definizione è la seguente.

Essendo {a_hk} la matrice di un gioco m×n, a_rs dicesi punto di sella e le strategie r-esima del giocatore I ed s-esima del II si dicono in equilibrio, se

a_hs ≤ a_rs ≤ a_rk per ogni h e per ogni k.  (2)

Questa definizione è puramente matematica e non implica alcuna descrizione o norma di comportamento effettivo. Se però si fissa l'attenzione proprio sul comportamento, benché non si possano trarre norme assolute, si può affermare che, subordinatamente all'adozione del criterio prudenziale, la scelta da parte del giocatore I (II) della propria strategia 'in equilibrio' gli garantisce in tutti i casi almeno il valore ars (-a_rs), anche se l'avversario sa con certezza che egli ha scelto quella strategia.

Con riferimento all'aspetto comportamentale le strategie in equilibrio si dicono strategie ottime e il valore v = a_rs del punto di sella viene senz'altro chiamato valore del gioco. Alcuni autori (per esempio De Finetti) chiamano minimax questo valore; altri riservano i nomi strategie ottime e valore del gioco al caso delle strategie miste (v. § 2f).

Un gioco dotato di punto di sella nell'ambito delle strategie pure si dice strettamente determinato; se invece ciò avviene nell'ambito delle strategie miste (v. § 2f) si dice determinato.

Una strategia ottima nel senso indicato, cioè relativamente al criterio prudenziale, diventa ottima in senso assoluto se l'avversario adotta una sua strategia ottima: il problema è avere questa informazione.

Un gioco può avere più di un punto di sella (e quindi più coppie di strategie in equilibrio), però, come si dimostra in modo elementare, il valore che corrisponde ai vari punti di sella è necessariamente il medesimo. Ne segue che il valore del gioco, se esiste, è univocamente determinato, mentre può avvenire che ciascun giocatore abbia a disposizione più di una strategia ottima. In tal caso la scelta è indifferente dal punto di vista del criterio prudenziale e può basarsi su altri criteri di convenienza.Un notevole significato che può assumere il valore del gioco (se esiste) è quello di 'valore d'arbitrato'. Supponendo infatti che due giocatori possano evitare di giocare rivolgendosi a un arbitro, incaricato di decidere quale somma un giocatore deve dare all'altro affinché il gioco non si effettui, questo valore d'arbitrato non potrà che coincidere col valore del gioco ars: se infatti fosse inferiore, il giocatore I rifiuterebbe, perché, giocando, può assicurarsi almeno a_rs, se fosse maggiore, rifiuterebbe l'altro per analoga ragione.

Un esempio bellico

Osserva O.J. Haywood jr. che un comandante militare può basare le proprie decisioni sulla capacità del nemico o sulle sue più o meno previste intenzioni e che le forze armate americane seguono il primo criterio. Ciò significa che, se una situazione militare può essere considerata come un gioco tra due persone, a somma nulla (il che è comunque discutibile), il criterio da seguire è quello di massimizzare il proprio livello di sicurezza; se entrambi i comandanti in contrapposizione seguono lo stesso criterio, le loro strategie dovranno essere quelle che realizzano il minimax, ove esista (per la bibliografia di Haywood, v. Luce e Raiffa, 1957, p. 64).

fig. 3

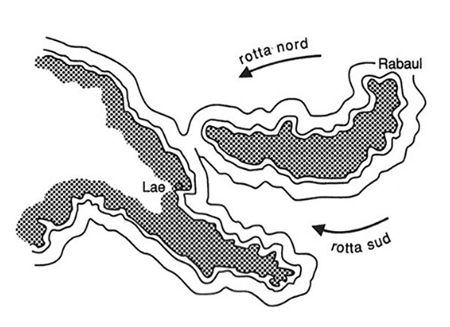
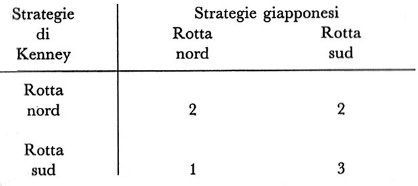
Un esempio è fornito dalla battaglia dell'Arcipelago di Bismarck nella seconda guerra mondiale (v. fig. 3). Il generale Kenney aveva avuto informazioni che un convoglio giapponese di truppe e rifornimenti sarebbe andato da Rabaul (Nuova Britannia) a Lae (Nuova Guinea). Il convoglio in questione poteva seguire due rotte, a nord o a sud della Nuova Britannia; il tempo di navigazione, in entrambi i casi, sarebbe stato di tre giorni. A nord vi era foschia quasi certa, a sud un'ottima visibilità. Kenney poteva concentrare gli aerei da ricognizione sulla rotta sud o su quella nord; una volta individuato, il convoglio poteva essere sottoposto a bombardamento sino all'arrivo a Lae. In termini di giorni di bombardamento la valutazione di Kenney era rappresentata dalla matrice seguente:

Si vede subito che esiste il punto di sella, corrispondente alle strategie rotta nord, rotta nord. La scelta di Kenney fu infatti rotta nord e i Giapponesi, che seguirono effettivamente la rotta nord, subirono gravi perdite. "Nonostante ciò - nota Haywood - non possiamo dire che il comandante giapponese abbia sbagliato decisione".

Giochi a perfetta informazione; strategie pure dominanti

Un gioco in cui ciascun giocatore conosce, in ogni momento, tutte le decisioni e tutti i risultati precedenti dicesi a perfetta informazione. Con riferimento alla rappresentazione ad albero (v. fig. 1), ciò significa che ogni insieme d'informazione contiene un solo vertice. In genere non appartengono a questa categoria i giochi di carte, se non altro perché un giocatore comunemente ignora (almeno inizialmente) quali siano le carte degli altri giocatori. Anche un gioco in cui entrino elementi aleatori potrebbe essere a perfetta informazione, ma in tal caso gli elementi della matrice del gioco sono valori medi di distribuzioni di probabilità. Non può esserlo invece un gioco in cui avvengano mosse simultanee (per esempio la morra). Esempi classici di giochi a perfetta informazione sono gli scacchi, la dama, il filetto, ecc.

In un gioco a matrice si dice che una strategia pura del giocatore I ne domina un'altra se tutti i suoi elementi sono maggiori o uguali a quelli corrispondenti dell'altra, e che la domina strettamente se vale sempre il segno >. Analoga definizione per le strategie pure del II, sostituendo 'maggiori o uguali' con 'minori o uguali' e il segno > con <. Una strategia pura dominata da un'altra comporta guadagni sicuramente non maggiori dell'altra, quale che sia la strategia dell'avversario: può quindi essere eliminata senza conseguenze da successivi ragionamenti (anche se poi si considerassero strategie miste: v. § 2f), e quindi la matrice si riduce di una linea (riga o colonna).

matrice 4

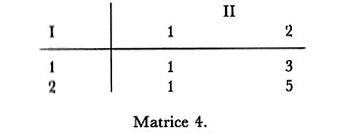
Va tuttavia rilevato che nel caso in cui una strategia sia dominata da un'altra, ma non strettamente, può venir perduta una possibile strategia 'ottima' (nel senso del minimax), che, pur equivalendo a quella dominante per il criterio prudenziale, è certo non preferibile.Il semplice esempio della matrice 4 chiarisce il rilievo. I due elementi della prima colonna, uguali a 1, sono entrambi punti di sella e quindi il giocatore I ha due strategie ottime; se elimina la prima riga, perché dominata dalla seconda, rimane con una sola strategia ottima, che ovviamente è preferibile a quella eliminata, ma non per motivi 'prudenziali'.

Un gioco a perfetta informazione gode di due importanti proprietà, di cui la seconda è immediata conseguenza della prima: a) la matrice di un gioco a perfetta informazione possiede sempre almeno una strategia dominata da un'altra; b) un gioco a perfetta informazione è strettamente determinato (cioè possiede un punto di sella nell'ambito delle strategie pure).

Che la seconda proprietà derivi immediatamente dalla prima segue dal fatto che, eliminando dalla matrice del gioco una strategia dominata, la nuova matrice rappresenta ancora un gioco a perfetta informazione e vale ancora la proprietà a): per ricorrenza ci si riduce a una sola riga e a una sola colonna, cioè a una matrice costituita da un solo elemento. Le prime sono ovviamente le strategie ottime, il secondo è il valore del gioco.

Ne segue, per esempio, che nel gioco degli scacchi, nell'ipotesi che i giocatori non commettano errori, una volta stabilito chi ha i 'bianchi' (cioè chi muove per primo), il gioco è finito. Tutto ciò non è vero in pratica, perché il gioco degli scacchi ha un numero così grande (benché finito) di strategie da rendere praticamente impossibile l'applicazione dei metodi descritti; in particolare, allo stato attuale delle conoscenze, non è noto il valore del gioco (vittoria del bianco, vittoria del nero, patta), ma si tratta di difficoltà tecniche che non influiscono sulla correttezza della conclusione che il gioco degli scacchi è strettamente determinato.

È notevole il fatto che la dimostrazione che il gioco degli scacchi è strettamente determinato sia stata data, su altre basi matematiche, sin dal 1913 da Zermelo (v., 1913) e sia valida per tutti i giochi tra due persone, a somma nulla e a perfetta informazione. Il teorema di Zermelo, benché abbia una dimostrazione 'non costruttiva', come tanti teoremi d'esistenza, ha certamente influito su importanti aspetti della teoria dei giochi, tra cui quello appena visto.

Strategie miste e teorema di von Neumann; riduzione alla programmazione lineare

Se nella matrice {a_hk} del gioco m×n non esiste un punto di sella, ognuno dei due giocatori (indipendentemente e all'insaputa l'uno dell'altro) potrebbe affidare la scelta della strategia da adottare a un sorteggio, con probabilità assegnate a piacere alle singole strategie. Dunque il giocatore I, che ha a disposizione m strategie pure, può fissare m numeri, x₁, x₂, ..., xm, che rappresentano le probabilità di sorteggio delle singole righe, cioè, come si usa dire, il vettore x=(x₁, x₂, ..., xm); analogamente il giocatore II può fissare a piacere il vettore y=(y₁, y₂, ..., yn) delle probabilità con cui sorteggerà le colonne. Si dice che il vettore x è una strategia mista del giocatore I e y è una strategia mista del II.

Dato il loro significato, le componenti dei vettorix, y sono soggette alle condizioni

(3) x_h ≥ 0 (h = 1, 2, ..., m)                    y_k ≥ 0 (k = 1, 2, ..., n) (3')

(4) ∑_hy_h = 1   ∑_ky_k = 1. (4')

Le strategie pure corrispondono ai vettori che hanno tutte le componenti nulle salvo una, che è uguale all'unità.

In corrispondenza a due fissate strategie x e y il valore medio del guadagno è

v(x, y) = ∑_hk a_hkx_hy_h. (5)

Nell'ambito delle strategie miste il minimax esiste certamente ed è univocamente determinato. Questo è il teorema di von Neumann.

Ciò significa che si può dimostrare che, nelle ipotesi (3)-(4´), sussiste l'uguaglianza

max_xmin_y v(x, y) = min_ymax_x v(x, y).  (6)

Il comune valore v* di queste due quantità è il 'valore del gioco' e due strategie miste x*, y* che lo realizzino diconsi strategie ottime.In termini più espliciti, ma equivalenti, il teorema di von Neumann afferma che esistono un numero v* e due strategie miste x*, y*, con v*=v(x*, y*), tali che

v(x, y*) ≤ v(x*, y) per ogni x e per ogni y. (7)

Si confronti la (7) con la definizione (2).

Indicando con xh la h-esima strategia pura del giocatore I (vettore con tutte le componenti nulle tranne la h-esima che è uguale a 1) e con y_k la k-esima strategia pura del II, dalla (7) si ricava, in particolare,

v(x_h, y*) ≤ v* ≤ v(x*, y_k) (h = 1, 2, ..., m; k = 1, 2, ..., n),  (8)

cioè, ricordando la (7) e la particolare forma delle x_h e y_k,

∑_k a_hky_k ≤ v* ≤ ∑_h a_hkx_h.  (8')

Si dimostra però che la (8) è non solo condizione necessaria, ma anche sufficiente affinché il numero v* e i vettori x*, y* siano rispettivamente il valore del gioco e le strategie ottime. Ne segue che per trovare il valore del gioco e le strategie ottime si può cercare di risolvere il sistema costituito dalle equazioni e dalle disequazioni seguenti nelle m+n+1 incognite x_h, y_k, v:

x_h ≥ 0 (h = 1, 2, ..., m)

∑_h x_h = 1

∑_h a_hk x_h ≥ v

y_k ≥ 0 (k = 1, 2, ..., n)

∑_k y_k = 1

∑_k a_hk y_k ≥ v.   (9)

Il procedimento sarebbe estremamente laborioso, perché si dovrebbero considerare tutti i sistemi che si traggono dalle (9) alternando nelle disuguaglianze miste i segni di uguaglianza e disuguaglianza in tutti i modi possibili (con qualche modesta esclusione, prevista dalla teoria, che rende il numero dei sistemi da considerare minore di 2²(m+ν)).

Un modo di aggirare questa difficoltà è quello di ricondurre il problema alla programmazione lineare.

Si supponga che gli elementi della matrice siano tutti positivi (e quindi anche il valore v* del gioco); ciò non lede la generalità dei risultati perché sussiste il seguente ovvio teorema.

Se gli elementi di una matrice {a_hk} si sottopongono a una trasformazione lineare α_hk=ma_hk+q, con m>0, le strategie ottime rimangono immutate e il valore v del gioco diventa V=mv+q.

Basta quindi aumentare tutti gli elementi della matrice di una opportuna quantità per renderli tutti positivi, se già non lo fossero.

Consideriamo le prime tre condizioni del sistema (9) e ricordiamo che queste possono essere verificate solo per valori di v non superiori a v*; in altre parole v* è il massimo valore di v che renda compatibili le prime tre delle (9). Posto allora zh=xh/v, si ottiene il valore del gioco e una strategia ottima x*=v*z* risolvendo il problema di programmazione lineare consistente nel rendere minima la forma

z = ∑_h z_h (10)

con le condizioni

z_h ≥ 0 (i = 1, 2, ..., m)

e

∑_h a_hk z_h ≥ 0 (k = 1, 2, ..., n).

Il minimo della forma lineare z non è altro che 1/v*.

La strategia ottima del giocatore II si ricava in modo analogo dalle ultime tre delle (9) e non è altro che il problema duale del precedente.

Giochi infiniti

Giochi con infinite strategie pure furono sistematicamente trattati per la prima volta da Ville (v., 1938), ma esistono precedenti esempi in Borel (v., 1921). Esempi di particolare importanza sono i giochi 'a tempo', in cui uno o entrambi i contendenti devono decidere l'istante in cui compiere un'azione, e i giochi di ripartizione.In generale per questi giochi non sussiste il teorema di von Neumann, ma esistono importanti casi particolari in cui è valido.

Per i giochi infiniti è opportuno dare una nuova definizione di valore del gioco, sostanzialmente sostituendo i concetti di massimo e minimo usati nei giochi finiti con quelli di estremo superiore ed estremo inferiore.

Essendo A l'insieme delle strategie pure α del giocatore I e B quello delle strategie pure β del II, il I guadagna v(α, β) (e il II perde v(α, β)), essendo v(α, β) una funzione di due variabili definita per ogni α ∈ A e per ogni β ∈ B. Il concetto di strategia mista può essere definito a vari livelli: come combinazione lineare convessa di un numero finito di strategie pure (come nel caso dei giochi finiti) o di una infinità numerabile di strategie pure, o come distribuzione di probabilità sull'insieme delle strategie pure, ecc. Comunque, detto X l'insieme delle strategie miste x di I e Y quello delle strategie miste y di II, e indicato con v(x, y) il valor medio del guadagno di I (perdita di II), se avviene

sup_xinf_y v(x, y) = inf_ysup_x v(x, y) = v (x ∈ X, y ∈ Y)  (6')

che sia (mentre in generale è sup_xinf_y v(x, y) ≤ inf_ysup_x v(x, y)), si dice che v è il valore del gioco.

In questo caso può darsi che non esista una strategia mista che assicuri al giocatore I di realizzare in media almeno il valore v (come nei giochi finiti), però, fissato ad arbitrio un numero reale ε>0, esiste sempre una strategia mista xe tale che

v(x_ε, y) ≥ v - ε,  (11)

per ogni y ∈ Y.

Analoghe le considerazioni per il giocatore II: fissato un ε>0 arbitrario, esiste sempre una strategia mista ye tale che per ogni x ∈ X.

Una importante classe di giochi che ammettono un valore, cioè per i quali sussiste la (6´), è costituita da quei giochi in cui uno dei due giocatori ha a disposizione un numero finito di strategie pure. Supponendo che sia il giocatore I, cioè che A sia finito, per lui esiste una strategia ottima x* tale che v(x*, y) ≤ v per ogni y ∈ Y, mentre, in generale, per il II sussiste la (12).

La stessa conclusione per l'esistenza del valore del gioco si ha quando un giocatore, per esempio il I, sa che, scelto ad arbitrio un ε>0, egli può limitare la sua scelta a un (opportuno) numero finito di strategie pure per costruire l'insieme X_ε di quelle miste, in modo che risulti |v(x_ε, y)-v(x, y)|<ε, con x_ε ∈ X_ε, per ogni x ∈ X e per ogni y ∈ Y.

Un particolare caso in cui trova applicazione questa proprietà è quello dei giochi sopra il quadrato unitario, cioè quelli in cui le strategie pure di entrambi i giocatori sono tutti i numeri reali dell'intervallo chiuso [0, 1], purché la funzione v(α, β) sia continua. Giochi sul quadrato unitario, in varie ipotesi sulla funzione v(α, β), sono stati ampiamente studiati (v., per esempio, Bohnenblust e altri, 1948 e 1950).

Giochi infiniti di diverso tipo sono quelli (a perfetta informazione) di durata infinita, cioè che prevedono infinite mosse. La loro importanza è soprattutto teorica e matematica, e il loro studio ha portato a interessanti sviluppi concernenti i fondamenti della matematica: in sostanza ha portato a individuare una contraddizione tra il teorema di Zermelo (sulla stretta determinazione dei giochi a perfetta informazione) e il suo assioma della scelta (v. Gale e Stewart, 1953; v. Mycielski e Steinhaus, 1964; v. Martin, 1975).

Giochi contro la 'natura'

Con questa denominazione si indicano 'giochi' in cui uno degli avversari è un operatore (economico, militare, ecc.), un decision maker, mentre l'avversario è uno stato della natura (il tempo che ci sarà domani in un dato luogo, uno sciopero dei trasporti preannunciato ma che può essere revocato, ecc.), e quindi un 'avversario' che non gioca personalmente contro di noi. Formalmente anche in questo caso la situazione può essere rappresentata da una matrice, come nel caso di giochi tra due persone. Basta identificare lo stato della natura come una partizione di eventi E_₁, E_₂, ..., En e il comportamento dell'operatore come l'insieme di tutte le decisioni per lui possibili, e che si escludono a vicenda, D_₁, D_₂, ..., Dm. L'operatore deve scegliere la sua decisione Dh prima di conoscere l'Ek che si verificherà: il risultato sarà il suo guadagno (algebrico) ahk in termini di denaro o di utilità. Comportarsi come prescrive la teoria dei giochi (cioè, se in questo caso esistesse il punto di sella, scegliere la strategia in equilibrio) sarebbe stravagante già nell'ambito delle strategie pure, dato che questa scelta era dettata essenzialmente dall'intento di contrastare il pensiero strategico dell'altro, e costituirebbe una rinuncia a servirsi delle proprie conoscenze ed esperienze; nell'ambito delle strategie miste poi sarebbe completamente senza senso, salvo il caso banale di un gioco indefinitamente ripetibile nelle stesse condizioni. Una delle giustificazioni dell'uso della teoria dei giochi in questo caso (almeno nell'ambito delle strategie pure) sarebbe la probabilità di avvicinarsi al valore maximin servendosi di dati oggettivi, per quanto oggettivi possano essere gli elementi della matrice.

3. Giochi tra due persone, a somma non nulla

Proprietà dei giochi a somma nulla che vengono a mancare

Se, in quanto precede, si toglie la restrizione 'a somma nulla', si ottiene un tipo di giochi, detti 'non strettamente competitivi', aventi caratteristiche nuove, profondamente diverse da quelle viste in precedenza. Va precisato che sarebbe più corretto parlare di giochi 'a somma non costante', perché è intuitivo, e facilmente dimostrabile, che giochi a somma costante si possono ricondurre immediatamente a quelli a somma nulla.

Essenziali proprietà dei giochi a somma nulla, non esplicitamente enunciate come tali perché implicite nel contesto, sono le seguenti.

A. Non è mai vantaggioso informare preventivamente l'avversario delle proprie decisioni (ovviamente, se si sceglie una strategia ottima, ciò non cambia il risultato, e può solo peggiorarlo in caso contrario).

B. Non avvantaggia i giocatori concordare un comune piano di gioco.

C. Se (x, y) e (x´, y´) sono entrambe in equilibrio, allora:

(x, y') e (x', y) sono entrambe in equilibrio; (13)

v₁(x, y) = v₁(x', y') = v₁(x', y) = v₁(x, y');

v₂(x, y) = v₂(x', y') = v₂(x', y) = v₂(x, y').  (14)

Con v₁ e v₂ si sono indicati i risultati del gioco per il primo e per il secondo giocatore, che devono essere distinti nel caso di gioco a somma non nulla. D. Se x è una strategia maximin per il giocatore I e y una strategia minimax per il II, (x, y) è una coppia di strategie in equilibrio e viceversa (per il teorema di von Neumann; notare che nel caso di giochi a somma non nulla si deve parlare di strategie maximin per entrambi i giocatori perché gli elementi delle due matrici indicano guadagni per entrambi).

Se vale la (13) si dice che le due coppie di strategie in equilibrio sono intercambiabili, se vale la (14) si dice che sono equivalenti.

Usando queste ultime definizioni, la proprietà D potrebbe esprimersi semplicemente affermando che in un gioco a somma nulla due coppie di strategie in equilibrio sono equivalenti e intercambiabili.

Per un gioco a somma non nulla possono risultare non valide tutte e quattro le proprietà elencate.

Si può mostrare questo fatto con un unico celebre esempio, denominato scherzosamente 'la battaglia dei sessi'.

matrice 5

Nel caso di somma non nulla non basta più ovviamente una matrice per indicare i guadagni di entrambi i giocatori; si usa però condensare le due matrici in un quadro unico, indicando per ogni coppia di strategie pure una coppia di numeri, di cui il primo indica il guadagno (algebrico) del giocatore I e il secondo quello del II. Il gioco accennato consiste in questo: due fidanzati vogliono uscire insieme una certa sera, ma lui preferisce andare al cinema e lei a una rivista; tuttavia entrambi preferiscono andare insieme piuttosto che separatamente. La situazione può essere descritta con la matrice 5, dove i valori numerici esprimono 'quantità di soddisfazione' in unità convenzionali (ovvero, si potrebbe anche dire, 'utilità'). Se ora l'uomo dichiara alla donna di essere assolutamente deciso ad andare al cinema e la donna sa che egli non ritorna mai sulle proprie decisioni, cioè è certa che l'uomo sceglierà la strategia 1, anch'ella avrà convenienza a scegliere la strategia 1 (perché sulla riga 1 è per lei preferibile la colonna 1). Il fidanzato dunque è avvantaggiato per aver dichiarato per primo, con sufficiente irremovibilità, la propria strategia: dunque non sussiste la proprietà A.

Che non sussista la proprietà B è ovvio: se le due persone parlano tra loro possono evitare i risultati (-1, -1), negativi per entrambi (a meno che non entrino in gioco questioni di puntiglio, ma ciò vorrebbe dire alterare la matrice del gioco). Per esempio essi potrebbero estrarre a sorte, con probabilità 1/2, le due coppie di strategie (1, 1) e (2, 2) che escludono, per entrambi, risultati negativi, e le rispettive utilità (medie) sarebbero per entrambi uguali a 3/2. Questo risultato è escluso se i due non possono parlare tra loro.

La definizione di 'strategie in equilibrio' (data dalla (2) per il caso particolare dei giochi a somma nulla) deve essere ovviamente modificata per il caso dei giochi a somma non nulla.

Definizione. - Due strategie tali che per ognuno dei due giocatori sia non vantaggioso modificare la propria strategia, nell'ipotesi che l'altro mantenga la propria, si dicono in equilibrio. (15) Evidentemente le strategie ottime nei giochi a somma nulla sono in equilibrio anche secondo questa definizione.

Sussiste il seguente teorema.

Teorema (v. Nash, 1951). - Ogni gioco non cooperativo con un numero finito di strategie pure possiede almeno una coppia di strategie miste in equilibrio. (16)

Si vede subito, ora, che non vale la proprietà C (v. matr. 5): la coppia di strategie pure (1, 1) è in equilibrio, e così pure quella (2, 2), però le coppie di strategie (1, 2) e (2, 1) non lo sono. Infine con facili calcoli si vede che le due strategie maximin (nell'ambito delle strategie miste) dei due giocatori non sono in equilibrio, il che crea quello stato di instabilità che, nel caso dei giochi a somma nulla, era stato sanato proprio dall'introduzione delle strategie miste.

Data l'importanza del fatto che sia o no possibile (o vietata) la comunicazione tra i due giocatori, vengono trattati come capitoli separati (salvo ovvie reciproche connessioni) i cosiddetti giochi cooperativi e giochi non cooperativi.

Problemi psicologici ed etici

Già le poche osservazioni fatte mostrano come nei giochi a somma non nulla divengano preponderanti gli aspetti psicologici, soggettivi, persino etici del problema, che rendono estremamente difficile una teorizzazione efficace.

Un esempio celebre è quello noto come 'dilemma del prigioniero' (elaborato da A.W. Tucker sulla base di una prima formulazione di M.M. Flood della Rand Corporation). Due uomini sono incolpati di aver commesso insieme un grave delitto, ma il pubblico ministero sa che non vi sono prove sufficienti per condannarli. Egli li esorta (separatamente) a confessare: se uno solo confessa, avrà una pena particolarmente lieve come premio per la sua collaborazione, mentre l'altro avrà quella massima; se confessano entrambi avranno una pena inferiore alla massima, ma tuttavia severa; se nessuno dei due confessa potranno essere condannati per un reato minore (per esempio possesso illegale di armi) e la pena sarà ovviamente leggera, però maggiore di quella che costituirebbe il 'premio di collaborazione' prima menzionato. Un esempio concreto è dato dalla seguente matrice, dove la strategia 1 significa per entrambi i giocatori 'non confessare', quella 2 'confessare' e i risultati sono anni di detenzione. Traducendo questi risultati in unità convenzionali di utilità (fatta variare tra 0 e 1) si ottiene una matrice del tipo seguente.

Nell'ipotesi non cooperativa, cioè se i due prigionieri non possono comunicare tra loro, si vede subito che per ciascuno dei due la strategia 2 domina, in senso stretto, la 1 (fissata la strategia di uno dei due, il massimo dell'utilità dell'altro corrisponde alla strategia 2). Dunque, avendo entrambi lo scopo di massimizzare la propria utilità, resta univocamente determinata la coppia di strategie - in tal senso - razionali: (2, 2). Ma avviene il seguente paradosso: se entrambi i giocatori si comportano in modo 'irrazionale' (cioè scelgono la strategia 1, 'non confessare') ne traggono un vantaggio.

Nell'ipotesi cooperativa, cioè se i due giocatori possono comunicare tra loro per pattuire, di comune accordo, una linea di condotta, la situazione è ancora peggiore. Il risultato di un accordo non può che essere la coppia di strategie (1, 1); ma ciascun giocatore, dopo aver fatto il patto di non confessare, si accorge che gli riesce vantaggioso mancare al patto, che l'altro vi si attenga oppure no. Su queste basi si presenta dunque inevitabile il doppio 'doppiogioco' (fare il patto (1, 1) per poi tradirlo da parte di entrambi), con la conseguenza di ottenere un risultato per entrambi peggiore. Nel contesto di questo gioco 'tradire un patto' è solo una possibile mossa, non fanno parte del discorso concetti come quelli di fiducia, onestà, lealtà. Nessuna meraviglia, in ambiente carcerario; sfortunatamente molte situazioni politiche (per esempio la corsa agli armamenti) ed economiche (concorrenza, ecc.) presentano lo stesso schema e spesso lo stesso triste risultato (per commenti pertinenti e profondi v. De Finetti, 1969).

Un'analisi di questo dilemma con una dilatazione delle strategie pure, in cui ogni giocatore considera le decisioni dell'avversario come altrettante strategie ('metagiochi', 'metastrategie'), dovuta a N. Howard (v., 1971), non supera, in sostanza, il problema fondamentale della fiducia.

Per i giochi a somma non nulla e non cooperativi sono stati proposti vari tipi di 'soluzioni', tutte più o meno discutibili e comunque subordinate a particolari proprietà della matrice. Per esempio un gioco è risolubile secondo Nash se, scelte comunque due coppie di strategie in equilibrio, esse sono intercambiabili. La soluzione, in tal caso, è costituita dall'insieme di tutte le strategie in equilibrio e, poiché non è richiesta l'equivalenza, il gioco potrà avere per ogni giocatore un valore superiore e un valore inferiore, con ovvio significato dei termini. Il dilemma del prigioniero è risolubile secondo Nash (perché ha un'unica coppia di strategie in equilibrio), per quanto discutibile possa essere la soluzione; non lo è la battaglia dei sessi, che possiede due coppie di strategie in equilibrio, non intercambiabili. Esistono altre definizioni di 'soluzione', e spesso giochi 'risolubili' in un senso non lo sono nell'altro.

Nel caso dei giochi cooperativi la ricerca di una 'soluzione' è complicata dal fatto che a un certo punto intervengono i ricordati aspetti psicologici e le tappe di una eventuale contrattazione. Una prima soluzione è stata proposta da von Neumann. Considerato l'insieme (chiuso e convesso) di tutte le coppie di utilità (u, v) conseguibili con strategie miste concordate, diciamo che una coppia domina un'altra se entrambi i suoi termini sono non minori dei corrispondenti dell'altra. Si conservino allora solo le coppie non dominate da altre (il che è naturale, dato che scartare le coppie dominate è vantaggioso per entrambi): l'insieme che rimane è un insieme di punti di ottimo paretiano, e il gioco, limitato a questo insieme, è strettamente competitivo. Da questo insieme si tolgano infine tutte le eventuali coppie che, per l'uno o per l'altro giocatore, comportano risultati inferiori al maximin che ognuno potrebbe conseguire in modo non cooperativo. L'insieme rimasto, detto insieme di negoziazione, costituisce la 'soluzione' del gioco cooperativo secondo von Neumann.

Per giungere a una soluzione costituita da un'unica coppia di utilità si può ricorrere, secondo l'impostazione di Nash (v., 1950), a uno schema d'arbitrato, cioè a una regola che dovrebbe seguire un arbitro scelto dai giocatori, regola basata su opportuni assiomi ritenuti da essi equi e accettabili. Nash stesso fornisce un insieme di assiomi molto ragionevole e dimostra che, se si accettano, la soluzione è unica (il che comporta che, in questo caso, non è più necessario un arbitro!). Essa è fornita dalla coppia di utilità uo, vo) che rende massimo il prodotto (u-υ*) (v-v*), ove con u* e v* si indicano i valori maximin dei due giocatori nell'ambito non cooperativo. La procedura usata è nota come procedura di Shapley perché, con lieve generalizzazione, è l'applicazione di un caso molto particolare del valore di Shapley di un gioco tra n persone (v. Shapley, 1953). La procedura di Nash (si tratta formalmente sempre della stessa) tiene invece conto del fatto che in alcuni casi è coerente assumere, come punto di partenza della procedura (statu quo), non i valori u* e v*, cioè i maximin, ma certi altri valori (individuati da opportune strategie di minaccia), rimanendo immutata, dopo questa sostituzione, la procedura e la forma del risultato.

Deve infine essere ricordata una impostazione, ancora di Nash, tendente a costruire modelli non cooperativi di giochi cooperativi, nota come 'programma di Nash' (v. Nash, 1951). Il programma ha avuto alcuni recenti interessanti contributi (v. Harsanyi, 1982; v. Harsanyi e Selten, 1972; v. Rubinstein, 1982).

La teoria dei giochi a somma non nulla considera molti altri argomenti - per esempio i pagamenti collaterali, che sono abbastanza spontanei, anche se forse proibiti, in questioni di appalti - e ha svariate applicazioni: economiche (duopolio, ecc.), sociali (contratti tra sindacati e datori di lavoro), militari, ecc. Comunque una delle maggiori debolezze di tutta la teoria dei giochi, e in particolare di questo caso, sta nella valutazione delle utilità dell'avversario e nel fatto, abbastanza ovvio, che un 'gioco' incomincia spesso proprio falsando, agli occhi dell'avversario, il valore delle proprie utilità.

Giochi ripetuti

In quanto precede si intende che i giochi considerati vengono giocati ciascuno una volta sola (come è inevitabile se si tratta di situazioni irripetibili). Anche se il gioco è privo di elementi aleatori, il valore del gioco nell'ambito delle strategie miste è un valor medio e non l'effettivo risultato. Ciò comporta qualche perplessità nell'uso delle strategie miste (ottime), e l'unica loro giustificazione sul piano pratico, per ciascuno dei giocatori, è costituita dall'ipotesi che l'avversario faccia altrettanto. Se il gioco è per sua natura ripetibile, si può considerare il 'supergioco' costituito da n iterazioni di questo. Se il gioco è a somma nulla, anche il supergioco risulta a somma nulla e l'uso ripetuto di strategie ottime nei singoli giochi costituisce una strategia ottima del supergioco. Inoltre il valore del gioco assume un significato pratico: diventa il limite, in probabilità, della media dei risultati se i giocatori usano le loro strategie ottime.

Diversa è la situazione nel caso di giochi a somma non nulla, sia nel caso non cooperativo che in quello cooperativo. Nel primo caso le successive informazioni acquisite sul comportamento dell'avversario costituiscono la base per una sorta di cooperazione; nel secondo (si pensi a una opportuna versione ripetibile del dilemma del prigioniero) la ripetibilità può portare a un comportamento 'leale' per la possibilità che ogni giocatore ha di punire l'altro al passo successivo.

4. Giochi tra più di due persone

La differenza tra giochi tra due persone e giochi tra n persone, con n≤3, non è di semplice complicazione formale, ma di natura qualitativa, a causa della possibilità di 'coalizioni', cioè di formazioni di sottoinsiemi della totalità degli n giocatori, in ciascuno dei quali si prendono accordi per guadagnare complessivamente di più e per ripartirsi poi questo 'di più' secondo regole interne al gruppo. Ne risulta una teoria profondamente diversa da quella dei giochi tra due persone (dove le uniche coalizioni possibili sono di natura impropria, cioè costituite dai singoli giocatori o dalla loro totalità).

La complessità della situazione, dovuta non solo a tutte le varianti già viste per due giocatori (somma nulla o non nulla, ecc.) è aumentata dal fatto che, volendo trattare realisticamente situazioni economiche, sociali, ecc., diventano poco interessanti i giochi in cui i risultati sono di natura monetaria (o trasformazioni banali di importi in termini di utilità), sicché sorge il problema della trasferibilità dell'utilità o della non trasferibilità dell'utilità, che dà luogo a due distinte parti della teoria: TU-giochi e NTU-giochi. Inoltre le complicazioni crescono comunque in modo fantastico al crescere di n, non solo per il crescere del numero delle possibili coalizioni, ma per il fatto che si presentano sempre nuove circostanze qualitativamente diverse da quelle già viste. Molte impostazioni, infine, possono essere sospettate di quel difetto caratterizzato da Good con il termine adhockeries (per De Finetti adhoccaggini: v. De Finetti, 1970, vol. I, p. 18), che indica costruzioni concettuali in cui le ipotesi più che essere realistiche servono a consentire sviluppi comodi ed eleganti della teoria.

Anche i vari numerosi tipi di soluzioni proposte, e la loro natura, lasciano insoddisfatti molti studiosi e molti utilizzatori. Tuttavia si deve riconoscere che oggi la parte più importante per le scienze economiche e sociali è costituita proprio dalla teoria dei giochi tra più di due persone.

La letteratura recente su tali giochi è vastissima ed è impossibile darne notizie esaurienti; qui verranno ricordati solo pochi punti fondamentali della teoria.Per i giochi non cooperativi sussistono immutate la definizione (15) e il teorema (16), relativi a due giocatori, salvo l'ovvio cambiamento dovuto al passaggio da 2 a n.

Definizione. - In un gioco tra n persone, n strategie tali che per ognuno degli n giocatori sia non vantaggioso modificare la propria strategia, nell'ipotesi che gli altri n-1 mantengano la propria, si dicono 'in equilibrio'. (15′)

Teorema (v. Nash, 1951). - Ogni gioco non cooperativo con un numero finito di strategie pure possiede almeno una n-pla di strategie miste in equilibrio. (16′)

Nel seguito, per evitare delicate precisazioni che potrebbero scadere nella polemica, si supporrà che le utilità in gioco siano importi di denaro: u(x)=x, ove x indica un importo.

Se il gioco è non cooperativo i ragionamenti si riconducono agevolmente al caso di due persone, pensando che ogni giocatore può conseguire il valore che otterrebbe se l'insieme degli altri n-1 giocatori fosse considerato come un unico avversario.

Un primo, fondamentale capitolo è costituito dai giochi cooperativi (con pagamenti collaterali ammessi) a somma costante K (in particolare, K=0, a somma nulla). Indicando con N l'insieme degli n giocatori, con S un qualunque sottoinsieme non vuoto e con @S il suo complementare, la peggior situazione che può incontrare la coalizione S è che anche i rimanenti giocatori si uniscano formando la coalizione @S. Il gioco si riduce in tal caso a un gioco tra due persone, a somma nulla, tra S e @S, e quindi esiste, per il teorema minimax, un valore del gioco v(S) che dipende dalla coalizione S e che gode delle note proprietà (S può assicurarsi come minimo il risultato - medio - v(S) e @S può far sì che quel risultato non superi v(S)). Risulta quindi definita una funzione d'insieme v(S) su tutti i sottoinsiemi di N; essa deve verificare le seguenti proprietà:

1) v(N) 0 K (gioco a somma costante K);

2) v(S) = K - v(@S), per ogni sottoinsieme S di N;

3) v(Φ) = 0, dove Φ è l'insieme vuoto;

4) v(R⋃S) ≥ v(R) + v(S) per ogni R, S ∈ N.

La 3 è conseguenza delle prime due; la 4 esprime il fatto, ben accettabile, che una coalizione più ampia non può peggiorare il risultato della somma delle componenti.

La funzione d'insieme v(S) dicesi funzione caratteristica del gioco a somma costante da cui deriva. In virtù della 4 la v(S) è detta superadditiva. Si dimostra che, data una funzione verificante le condizioni 1-4, esiste sempre un gioco a somma costante K di cui v(S) è la funzione caratteristica: ciò significa che la definizione di una funzione caratteristica costituisce un terzo modo di sintetizzare un gioco a somma costante, dopo quella estensiva e quella normale.

Formatesi le coalizioni, l'importo xh che spetterà a ogni giocatore h (h=1, 2, ..., n) è costituito da ciò che gli compete in base alla forma normale del gioco con l'aggiunta di quella quota in più che è stata concordata al momento della formazione dell'eventuale coalizione di cui è entrato a far parte. Si dice imputazione ogni vettore x di n numeri (guadagni algebrici) (x_₁, ..., x_n) che sono astretti alle ovvie condizioni x_h ≥ v({h}), Σx_h = v(N), ove con {h} si indica l'insieme costituito dal solo giocatore h.

Se in un gioco avviene che x_h=v({h}) per ogni h e per qualsiasi coalizione, se cioè è indifferente ai fini del risultato che un giocatore si associ o no con altri per concordare le strategie, il goco si dice inessenziale e non presenta maggior interesse dei giochi non cooperativi. Per contrapposto si dicono essenziali quei giochi per i quali non è identicamente vera la x_h=v({h}).

Se S è una coalizione e x e y due imputazioni tali che

∑_h∈Sx_h ≤ v(S)   (17)

(condizione di ammissibilità)

e

x_h > y_h per ogni h ∈ S     (18)

(condizione di preferibilità)

si dice che x domina y secondo la coalizione S.

Definizione. - Si dice che una imputazione x domina una imputazione y se esiste almeno una coalizione S non vuota per la quale sono verificate le (17) e (18).

In un gioco essenziale a somma nulla (o a somma costante) non esistono imputazioni che non siano dominate da altre: poiché l'insieme delle imputazioni non dominate da altre si chiama nucleo (in inglese core), si può esprimere quanto affermato dicendo che il nucleo di un gioco a somma nulla è vuoto. Solo giochi a somma non costante, modificando in modo opportuno la definizione di funzione caratteristica (cadono le precedenti condizioni 1 e 2), possono possedere un nucleo non vuoto.

Ciò non esclude la possibilità di definire una 'soluzione' per giochi essenziali a somma costante. Per mostrarlo usiamo un esempio classico cui si può sempre ricondurre un gioco essenziale fra tre giocatori a somma costante. Si abbia

v([1]) = v({2}) = v({3}) = 0,

v([1, 2]) = v({1, 3}) = v({2, 3}) = 1,

v([1, 2, 3]) = 1 (somma costante uguale a 1).

Il gioco può esprimersi a parole in modo molto semplice: se i giocatori non formano alcuna alleanza nessuno vince alcunché; se due giocatori (poco importa quali) si alleano contro il terzo vincono (insieme) 1 (unità monetaria) e il terzo nulla. I due giocatori che si coalizzano hanno ruoli simmetrici ed è quindi ragionevole che si dividano a metà l'importo 1; ne risultano come 'naturali' le tre imputazioni, il cui insieme conveniamo di chiamare F,

(1/2, 1/2, 0), (1/2, 0, 1/2), (0, 1/2, 1/2).

Esse godono di una particolare proprietà: ogni imputazione in F è dominata da una o più imputazioni non in F, ma è anche vero che per ogni imputazione non in F ne esiste una in F che la domina. Quest'ultimo risultato, che si dimostra agevolmente, è molto notevole, perché vi sono solo tre imputazioni in F, mentre ve ne sono infinite non in F. Inoltre nessuna delle imputazioni in F domina qualcuna delle altre due. Per questo motivo von Neumann assunse l'insieme F come 'soluzione' del gioco.

Esiste tuttavia un'altra proprietà che assicura alle imputazioni di F una particolare stabilità, ma che von Neumann non ritenne necessario menzionare in aggiunta alla prima (forse perché non formalizzabile in termini matematici). Si tratta di quanto segue. Supponendo che si sia formata la coalizione (1/2, 1/2, 0) il giocatore 3 (subdolo diavolo!) può offrire al giocatore 2 (per esempio) di sciogliere la precedente coalizione e formare coalizione con lui con l'imputazione (0, 3/4, 1/4): con ciò guadagnano entrambi i giocatori 2 e 3 mentre 1 rimane a 0. Però è naturale che a questo punto il giocatore 1 offra al 3 di coalizzarsi con l'imputazione (1/2, 0, 1/2): ancora una volta i due nuovi coalizzati, 1 e 3, ci guadagnano e resta escluso il giocatore 2 che aveva ceduto alla tentazione. Questo ragionamento assicura una particolare stabilità a una qualunque delle imputazioni di F, una volta che si sia formata.

5. Esempi di applicazioni all'economia

Oligopolio (duopolio)

Come è ben noto, l'oligopolio è una struttura di mercato caratterizzata dalla presenza di pochi venditori (produttori) di un certo bene o servizio, di fronte alla concorrenza perfetta tra compratori. Non solo come definizione, ma anche come trattazione teorica, il caso di due soli venditori, cioè del duopolio, può essere considerato come caso particolare dell'oligopolio, e le conclusioni cui si perviene possono, nella sostanza, essere estese al caso di più di due (ma comunque pochi) venditori. La precisazione 'pochi' significa che ognuno dei venditori è una parte non trascurabile del loro insieme. In questi brevi cenni sarà dunque sufficiente limitarsi al duopolio.

Indicando con x la quantità prodotta dal duopolista I, con y quella prodotta dal II, con F(x, y), G(x, y) i rispettivi profitti, con C₁ e C₂ i costi di produzione (funzione, per ciascun produttore, della quantità da lui prodotta) con P(x+y) il prezzo (funzione della quantità totale immessa sul mercato dai due produttori), sarà

F(x, y) = P(x+y)x-C₁(x)   (19)

G(x, y) = P(x + y)Y - C₂(y).  (20)

Secondo l'impostazione di Cournot, ciascuno dei due duopolisti cerca di massimizzare il proprio profitto nell'ipotesi che la produzione dell'altro rimanga costante.

Indicando con F_x la derivata parziale di F rispetto a x, ecc., le condizioni necessarie (e in genere anche sufficienti) di massimo, nelle ipotesi poste, sono F_x(x, y)=0, G_y(x, y) = 0 cioè

P(x + y) = C'₁(x) - P_x(x + y)x   (21)

P(x + y) = C'₂(y) - P_y(x + y)y.  (22)

Si può pensare che la (21) sia la definizione implicita della funzione x=X(y) che descrive la scelta ottimale della quantità prodotta dal I, data quella del II, e che la (22) definisca la funzione y=Y(x) con analogo significato per il II. Le due curve di equazione x=X(y) e y=Y(x), sul piano (x, y), sono dette curve di reazione dei due duopolisti e il loro punto d'incontro fornisce, con le sue coordinate xC_₉, yC_₉, il cosiddetto equilibrio di Cournot.

Un certo perfezionamento viene apportato a questo tipo di comportamento dal modello di Stackelberg.

Si fa la seguente ipotesi: uno dei due duopolisti, per esempio il I, ritenendo che l'altro segua il modello di Cournot, e cioè faccia uso della curva di reazione y=Y(x) sopra definita, decide di tener conto di questa congettura nel massimizzare il proprio profitto F(x, y) e quindi non può più ritenere y costante, ma deve determinare il massimo di F[x, Y(x)]. La condizione (21) cambia in modo ovvio diventando

P(x + y) = C'₁(x) - P_x(x + y) [1 + Y' (x)] x,   (23)

e così cambierebbe la (22) se a fare il predetto ragionamento fosse il II: la sua funzione di profitto diverrebbe G(X(y), y) e la (22) stessa

P(x + y) = C'₂(y) - P_y(x + y) [X' (y) + 1] y.   (24)

Se dunque è il I a fare tale ragionamento, la sua curva di reazione cambia in base alla (23) e diventa la curva di reazione di Stackelberg (per il I). Se l'altro si comporta realmente come congetturato dal I, le due curve di reazione, quella di Stackelberg per il primo e quella di Cournot per il secondo, si incontrano in un punto che, con le sue coordinate, individua il cosiddetto equilibrio di Stackelberg (per il I). Analoghe considerazioni scambiando le veci dei due duopolisti. In letteratura il duopolista che usa la curva di reazione di Stackelberg viene detto leader (parola ormai di uso internazionale) e quello che usa la curva di reazione di Cournot viene detto satellite (follower). Se sia più conveniente essere leader o satellite dipende dalle rispettive funzioni di costo. Ognuno dei due duopolisti può decidere se essere leader o satellite. Se entrambi decidono di comportarsi da satellite si ha l'equilibrio di Cournot; se uno decide di essere leader e l'altro satellite si ha l'equilibrio di Stackelberg (e naturalmente, in genere, i due punti di equilibrio - se è leader il I o se è leader il II - non coincidono). Infine, se entrambi decidono di essere leaders, si ha il cosiddetto disequilibrio di Stackelberg (Stackelberg warfare).

Questa sommaria descrizione del duopolio, in cui si è sorvolato su numerose precisazioni economiche e matematiche, è tuttavia sufficiente per intuire subito che esso è interpretabile come un gioco tra due persone, a somma non nulla; e nella versione riportata si tratta di un gioco non cooperativo.

matrice 7

Ognuno dei due giocatori ha due strategie pure possibili: comportarsi da satellite oppure da leader. Indicandole rispettivamente con S e con L si ottiene schematicamente la  matrice 7. Si osservi che in questa matrice si intendono inseriti non i valori delle coordinate dei punti di equilibrio (o disequilibrio), bensì i valori che F(x, y) e G(x, y) assumono in tali punti.

Il semplice esempio numerico che segue non solo chiarirà quanto precede, ma per la particolare ipotesi che faremo - che le funzioni di costo siano uguali - porterà a un risultato particolarmente interessante.

Supponiamo che la funzione prezzo sia lineare e così pure le funzioni di costo, uguali per i due produttori:

funzione prezzo   P(q) = 30 - 2q

(q = quantità eccessiva)

funzioni di costo    C₁(q) = C₂(q) = 6q + k

(q  quantità individuale).

Ovviamente, comunque si fissino i coefficienti, la quantità non negativa q si deve supporre tale da rendere P(q)>0. La costante k che figura nelle funzioni di costo non ha rilievo nei calcoli che seguono e si può supporre nulla.

Con queste posizioni le (19)-(24) diventano (dopo facili calcoli):

F(x, y) = [30 - 2(x + y)]x - 6x    (19')

G(x, y) = [30 - 2(x + y)]y - 6y    (20')

2x + y = 12 (curve di reazione di Cournot)  (21')

x + 2y = 12      (22')

3x + 2y = 24 (curve di reazione di Stackelberg)  (23')

2x + 3y = 24.  (24')

Risolvendo il sistema {21′, 22′} si trova il punto d'equilibrio di Cournot: x = 4, y = 4. Dal sistema {23′, 24′} si trae il punto di disequilibrio di Stackelberg: x = 4, 8,y = 4, 8. Infine dai sistemi {23′, 22′} e {24′, 21′} si ottengono i punti d'equilibrio di Stackelberg, rispettivamente essendo leader il I oppure il II 'giocatore': x = 6, y = 3 nel primo caso, x = 3, y = 6 nel secondo.

7′

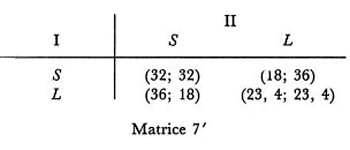
Sostituendo questi valori numerici nelle (19′) e (20′), la matrice 7 diventa la 7′.

Si osservi che la matrice 7′ ha la stessa struttura di quella del dilemma del prigioniero, con le stesse conseguenze.

Soluzione di un mercato con un venditore e due compratori

Come notano Luce e Raiffa (v., 1957, p. 207), il noto esempio che segue "è particolarmente adatto a scopi illustrativi, perché è sufficientemente semplice per essere analizzato [anche] con argomenti economici basati sul senso comune".

Il giocatore 1, il venditore, è disposto a vendere un oggetto indivisibile per un importo non inferiore ad a; i due compratori, giocatori 2 e 3, valutano l'oggetto rispettivamente b e c. Si suppone, per fissare le idee, b≤c e, affinché una trattativa abbia senso, a<b.

Determiniamo la funzione caratteristica del gioco. Risulta v({1}) = a, perché 1 possiede l'oggetto, da lui stesso valutato a, ma non può essere certo di venderlo e quindi valutarlo di più. Per i compratori, che non sono obbligati a partecipare al mercato e non possiedono l'oggetto, si ha v({2}) = v({3}) = 0. Se si forma la coalizione {1, 2}, l'oggetto è in possesso della coalizione e non può essere alienato a meno di b, perché se 1 fosse tentato di farlo, 2 gli darebbe quanto occorre per assicurarsi l'oggetto, che quindi rimarrebbe in possesso della coalizione {1, 2}. Dunque v({1, 2})=b. Con ragionamenti simili rimane fissato il valore di v per gli altri casi e la funzione caratteristica rimane quindi definita come segue:

v({1}) = a,        v({2}) = v({3}) = 0,

v({1, 2}) = b,     v({1, 3}) = c,

v({2, 3}) = 0,     v({1, 2, 3}) = c.    (25)

Una imputazione per questo gioco è, per definizione, una qualunque terna di valori (x_₁, x_₂, x_₃) che verifichi le seguenti relazioni:

x₁ + x₂ + x₃ = c,   x₁ ≥ a,    x₂ ≥ 0, x₃ ≥ 0.  (26)

Allo scopo di dare ulteriori precisazioni sulle imputazioni che possono presentarsi, ci si può servire sia di ragionamenti basati sul 'buon senso' economico, sia su quanto suggerisce la teoria dei giochi.

Poiché è in vendita un solo oggetto indivisibile, in base al buon senso si deduce che uno solo dei compratori otterrà l'oggetto, e naturalmente sarà il più forte, cioè il 3, a meno che sia b=c (caso che può essere considerato a parte); infatti egli può ottenere l'oggetto offrendo qualche cosa più di b, escludendo il 2 dalla competizione.

Dunque le sole imputazioni che possono presentarsi, secondo questo ragionamento, sono quelle che verificano le seguenti ulteriori condizioni:

b ≤ x₁ ≤ c,   x₂ = 0,   x₃ = c - x₁;    (27)

naturalmente l'ultima delle (27) è conseguenza della precedente e della prima delle (26).

Un primo modo di utilizzare la teoria dei giochi può consistere nel considerare tutte le imputazioni che costituiscono il nucleo. Si dimostra il fatto notevole che tutte e sole le imputazioni del tipo (27), trovate col 'buon senso', sono proprio quelle che costituiscono il nucleo. Se però si passa al concetto di soluzione del gioco, nel senso di von Neumann, si vede che all'insieme delle imputazioni costituenti il nucleo si deve aggiungere l'insieme di tutte quelle della forma

[x, f(x), c - x - f(x)],  a ≤ x ≤ b,   (28)

dove f(x) è una qualunque funzione decrescente di x, tale che

0 ≤ f(x) ≤ c - x.

Un esempio è fornito dalla seguente imputazione:

[x, (c - x)/3,  2(c - x)/3],  a ≤ x ≤ b.  (28')

Una interpretazione concreta di questo tipo di imputazioni si può avere pensando che i giocatori 2 e 3 formino una coalizione e si accordino affinché il giocatore 1 non riceva più di b. Con ciò la coalizione entra in possesso dell'oggetto a un prezzo x≤b; il valore effettivo x dipende dall'abilità di negoziazione di 1. Infine il possesso definitivo dell'oggetto dipende da accordi tra 2 e 3 e dal compenso che l'uno offre all'altro per questo scopo.

Una osservazione di natura matematica: il fatto che nel concetto di soluzione entrino altre imputazioni oltre a quelle del nucleo non deve meravigliare. Infatti il nucleo è per definizione l'insieme di tutte le imputazioni che non sono dominate da altre, ma ciò non significa affatto che queste imputazioni dominino tutte quelle che non sono nel nucleo; invero, nel caso esaminato, le imputazioni (28) non sono dominate da alcuna imputazione del nucleo, ma tuttavia non fanno parte del nucleo perché sono dominate da altre fuori del nucleo.

6. Conclusioni

I giochi tra due persone, in particolare quelli strettamente competitivi (v. cap. 2), nei primi anni in cui fiorì la teoria dei giochi ne furono una parte privilegiata (v. Luce e Raiffa, 1957, pp. 156-157); oggi avviene l'opposto e questa parte è considerata quasi come un capitolo irrilevante. "Tuttavia - come nota Aumann (v., 1987, p. 460) - lo studio del caso strettamente competitivo si è rivelato nel corso degli anni notevolmente fruttuoso: molti dei concetti e dei risultati generati in connessione con questo caso sono in realtà ben più ampiamente applicabili e sono diventati la pietra angolare della teoria più generale".

Notevoli riserve su molte applicazioni improprie della teoria sono state sollevate da molti studiosi, in particolare da De Finetti (v., 1969), che osserva come il fondamentale principio decisionale della massimizzazione dell'utilità sperata venga usato solo in modo parziale e del tutto tradito nel caso dei giochi 'contro la natura'.

Le risposte che la teoria dei giochi dà in molti problemi concreti, specie economici, sono spesso largamente insoddisfacenti, ma, come nota De Finetti (ibid., p. 126): "È sempre necessario - anche se non sempre viene fatto - riflettere non solo e non tanto su quello che una teoria o dottrina esplicitamente afferma e considera, quanto anche e più sui problemi che lascia aperti o addirittura apre e solleva, sui punti che lascia oscuri o che con la sua luce fa apparire più che mai confinati in un tagliente cono d'ombra". Ed è quanto mai opportuno chiudere queste considerazioni finali con una citazione di Rapoport, riportata dallo stesso De Finetti nel medesimo lavoro, che pur risalendo al 1962 è sempre attuale: "Il valore della game theory non sta nelle specifiche soluzioni che offre in situazioni altamente semplificate e idealizzate, che possono presentarsi in giochi veri e propri, ma difficilmente nella vita reale. Piuttosto il principale valore della teoria sta nel fatto che essa mette a nudo i differenti tipi di ragionamento che si prospettano in differenti tipi di conflitto". (V. anche Decisioni, teoria delle; Oligopolio; Programmazione lineare).

Bibliografia

Aumann, R.J., Game theory, in The new Palgrave dictionary of economics (a cura di J. Eatwell, M. Milgate e P. Newman), vol. II, London-Basingstoke 1987, pp. 460-482.

Blackwell, D., Girshick, M.A., Theory of games and statistical decision, New York 1954.

Bohnenblust, H., Dresher, M., Girshick, M.A., Harris, T.E., Helmer, O., McKinsey, J.C.C., Shapley, L.S., Snow, R.N., Mathematical theory of zero-sum two-person games with a finite or a continuum of strategies, Santa Monica, Cal., 1948.

Bohnenblust, H., Karlin, S., Shapley, L.S., Games with continuous convex pay-off, in Contributions to the theory of games (a cura di H.W. Kuhn e A.W. Tucker), vol. I, Princeton, N.J., 1950, pp. 181-192.

Borel, É., La théorie du jeu et les équations intégrales à noyau symétrique, in "Comptes rendus de l'Académie des Sciences", 1921, CLXXIII, pp. 1304-1308.

Borel, É., On games that involve chance and the skill of the players, in "Econometrica", 1953, XXI, pp. 101-115.

Borel, É., On systems of linear forms of skew symmetric determinants and the general theory of play, in "Econometrica", 1953, XXI, pp. 116-117.

De Finetti, B., Il rischio e le decisioni economiche, in "Quaderni dell'Istituto per gli Studi Assicurativi", 1954, XI, pp. 41-72.

De Finetti, B., Obiettività e oggettività: critica a un miraggio, in "La rivista trimestrale", 1962, I, 2, pp. 343-367.

De Finetti, B., La teoria dei giochi: cosa ci dice, su che cosa ci invita a riflettere, in Un matematico e l'economia, Milano 1969, pp. 105-143.

De Finetti, B., Teoria della probabilità, 2 voll., Torino 1970.

Gale, D., Stewart, F.H., Infinite games with perfect information, in Contributions to the theory of games (a cura di H.W. Kuhn e A.W. Tucker), vol. II, Princeton, N.J., 1953, pp. 245-266.

Harsanyi, J.C., Solutions for some bargaining games under the Harsanyi-Selten solution theory. I: Theoretical preliminaries; II: Analysis of specific games, in "Mathematical social sciences", 1982, III, pp. 179-191 e 259-279.

Harsanyi, J.C., Selten, R.A., A generalized Nash solution for two-person bargaining games with incomplete information, in "Management science", 1972, XVIII, pp. 80-106.

Howard, N., Paradoxes of rationality: the theory of metagames and political behavior, Cambridge, Mass., 1971.

Kuhn, H.W., Tucker, A.W. (a cura di), Contributions to the theory of games, vol. I, Princeton, N.J., 1950.

Kuhn, H.W., Tucker, A.W. (a cura di), Contributions to the theory of games, vol. II, Princeton, N.J., 1953.

Luce, R.D., Raiffa, H., Games and decisions: introduction and critical survey, New York 1957.

Martin, D.A., Borel determinacy, in "Annals of mathematics", 1975, CII, pp. 363-371.

McKinsey, J.C.C., Introduction to the theory of games, New York 1952.

Mycielski, J., Steinhaus, H., On the axiom of determinateness, in "Fundamenta mathematicae", 1964, LIII, pp. 205-224.

Nash, J.F. jr., The bargaining problem, in "Econometrica", 1950, XVIII, pp. 155-162.

Nash, J.F. jr., Non-cooperative games, in "Annals of mathematics", 1951, LIV, pp. 289-295.

Neumann, J. von, Zur Theorie der Gesellschaftsspiele, in "Mathematische Annalen", 1928, C, pp. 295-320.

Neumann, J. von, Morgenstern, O., Theory of games and economic behavior, Princeton, N.J., 1944.

Rubinstein, A., Perfect equilibrium in a bargaining model, in "Econometrica", 1982, L, pp. 97-109.

Shapley, L.S., A value for n-person games, in Contributions to the theory of games (a cura di H.W. Kuhn e A.W. Tucker), vol. II, Princeton, N.J., 1953, pp. 305-317.

Ville, J.A., Sur la théorie générale des jeux où intervient l'habilité des joueurs, in Traité du calcul des probabilités et de ses applications (a cura di É. Borel), vol. IV, Paris 1938, pp. 105-113.

Zermelo, E., Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, in "Proceedings of the fifth international congress of mathematicians", 1913, II, pp. 501-504.