giochi, teoria dei

giochi, teoria dei

giochi, teoria dei branca disciplinare che studia il problema della interdipendenza tra i soggetti partecipanti a un gioco, sia esso un negoziato politico, una strategia di mercato o un gioco di società (→ gioco). L’analisi dei comportamenti degli agenti che prendono parte al gioco è detta interazione strategica, all’interno di un qualsiasi contesto in cui un soggetto è portato a reagire in conseguenza del comportamento di un altro soggetto o simultaneamente a esso. La teoria dei giochi è stata elaborata dallo scienziato tedesco J. von Neumann nel 1944, che ne sviluppò le applicazioni economiche con l’economista statunitense O. Morgenstern (1902-77). La teoria dei giochi può anche essere considerata come parte della teoria delle decisioni, che analizza le situazioni in cui: a) tra le strategie disponibili al giocatore ve ne siano alcune che prevedono il suo ingresso, a certe condizioni, in una coalizione atta, a suo giudizio, a facilitare il raggiungimento dei suoi scopi o la difesa dei suoi interessi; b) nel valutare la probabilità dei vari eventi che reputa possibili, il giocatore debba tener conto delle scelte che potranno effettuare gli antagonisti. Nella misura in cui gli antagonisti sono tali consapevolmente, ciascuno di essi terrà presumibilmente conto, al momento della sua scelta, dell’analisi che a suo giudizio faranno della situazione gli altri.

I casi effettivamente discussi dalla teoria dei giochi sono convenienti idealizzazioni, che hanno permesso di esaminare in base a nuove prospettive molte situazioni di conflitto sia nell’economia (commercio internazionale, relazioni tra sindacato e industria ecc.) sia nella strategia politico-militare. Una prima drastica semplificazione viene conseguita con l’introduzione del concetto di strategia, cioè di una regola che prescriva come comportarsi in ciascuna delle situazioni in cui ci si può venire a trovare nel corso del gioco. Il compito di ogni giocatore si riduce allora, formalmente, alla scelta di una strategia. Accadrà inoltre, generalmente, che il risultato conseguito alla fine del gioco da ciascun giocatore dipenda, oltre che dall’insieme delle strategie scelte, anche da certi fattori aleatori esterni. Un’ulteriore semplificazione si ottiene sostituendo a ciascun risultato la sua previsione (→ speranza matematica) rispetto all’insieme dei fattori aleatori esterni. Ci si riduce così, formalmente, al caso in cui il risultato spettante a ciascun giocatore dipende unicamente e deterministicamente dall’insieme delle scelte di strategia effettuate. La teoria non tratta però della possibilità, pur realistica, che le valutazioni di probabilità dei diversi giocatori circa i fattori aleatori esterni non coincidano.

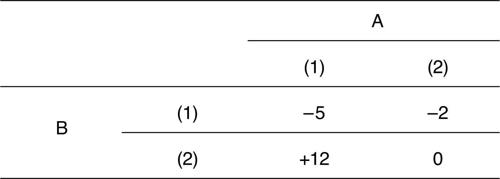
Il caso più semplice, ma al tempo stesso fondamentale, è quello del gioco tra due persone a somma zero, nel quale cioè un giocatore vince ciò che l’altro perde, e finito, nel quale cioè ciascuno dei due giocatori dispone di un insieme finito di strategie tra cui scegliere. La rappresentazione dei risultati conseguibili da ciascun giocatore viene effettuata, in termini di profitto di uno dei due, nella matrice del gioco che assume la forma riportata in figura.

I due giocatori, A e B, hanno due strategie possibili, (1) e (2), rappresentate per B dalle righe e per A dalle colonne della matrice; tali strategie si dicono più esattamente strategie pure. I risultati del gioco sono espressi in termini di profitto del giocatore A; si ha per esempio che se B usa la strategia (1), corrispondente alla prima riga, e A usa la strategia (2), corrispondente alla seconda colonna, il risultato del gioco consisterà in una perdita per il giocatore A pari a 2. Vale per questo caso il teorema del minimax, che può essere illustrato dalle seguenti considerazioni: se A sceglie la strategia (1) potrà vincere 12 nel caso B scelga la strategia (2), ma perderà 5 se B sceglie (1). Un comportamento prudenziale indurrà a scegliere la strategia (2), perché in tale caso la massima perdita possibile sarà minimizzata. Applicando il medesimo criterio prudenziale, B (che ha perdite esattamente uguali ai guadagni di A) sarà analogamente indotto a scegliere la strategia (2), a cui corrisponde una perdita nulla. In casi analoghi a quello considerato si suole dire che la combinazione ottima di strategie da parte dei due giocatori risponde al criterio del minimax: il giocatore A seleziona la colonna (strategia) nella quale figura il massimo dei risultati minimi; il giocatore B seleziona la riga (strategia) dove figura il minimo dei risultati massimi (infatti, i guadagni si riferiscono al suo oppositore). Dal punto di vista matematico la combinazione delle strategie ottime, quando è unica, individua nella matrice dei risultati il cosiddetto punto di sella. Con riferimento a questo, quando esiste, si individua la strategia ottima per ciascun giocatore e si enuncia il principio di impossibilità: né l’uno né l’altro dei giocatori può ottenere più di quanto possa assicurargli la strategia minimax. A partire dal gioco a somma zero tra due persone, la teoria viene ampliata col passare a considerare: giochi a somma non zero, dove gli interessi degli antagonisti possono in parte coincidere (per esempio, due imprese che concorrono per l’appalto di un certo lavoro; il profitto effettuabile dall’impresa vincitrice della gara è diverso dal profitto perduto dalla seconda, se i costi di realizzazione sono, come è naturale attendersi, differenti per le due imprese); giochi a somma zero tra n > 2 persone, che è possibile ricondurre al caso di due sole persone. Von Neumann e Morgenstern hanno infatti dimostrato che qualunque gioco a n persone e a somma non zero può essere ridotto a un gioco a n + 1 persone e somma zero e che quest’ultimo è una generalizzazione del caso particolare del gioco a due persone. Se però il gioco è essenziale, nel senso che coalizzandosi con altri un giocatore può modificare i risultati raggiungibili, la scelta tra le diverse coalizioni in cui può entrare e tra le ripartizioni del risultato globale conseguito da una coalizione conduce a considerare problemi di comunicazione, credibilità, negoziato, cooperazione, rescindibilità di patti ecc.

La varietà e la natura delle conclusioni cui portano i vari sistemi di ipotesi che si possono fare circa tali aspetti (per esempio la possibilità dì comunicare simultaneamente e istantaneamente, l’accettabilità del ricorso a un arbitro, il grado di coesione tra i membri di una coalizione, le regole etiche generalmente accettate ecc.), pur fornendo utili spunti di riflessione per lo studio di molti casi concreti, non permettono tanto di giungere alla scoperta di strategie vantaggiose per un giocatore qualsiasi, quanto piuttosto di porre in luce i limiti del concetto di razionalità individuale che sta alla base di gran parte delle teorie sul comportamento economico e politico. La teoria dei giochi trova applicazioni, oltre che in economia e nel campo delle strategie militari, anche in biologia, in particolare nello studio dell’evoluzione della specie. Essa ha punti di contatto con altre branche della matematica quali il calcolo delle → probabilità, la → statistica e la → programmazione lineare.