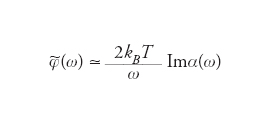teoremi di fluttuazione
teoremi di fluttuazione
Una relazione tra la reazione lineare di un sistema in equilibrio a deboli perturbazioni esterne e la correlazione temporale di fluttuazioni intorno all’equilibrio o più in generale fenomeni di fluttuazione. Il teorema di fluttuazione-dissipazione è stato stabilito nel 1951 da Herbert B. Callen e Theodore A. Welton e costituisce un ponte tra la meccanica statistica all’equilibrio e quella fuori dall’equilibrio. Esso si basa sull’osservazione fisica che la reazione di un sistema termodinamico a deviazioni del valor medio statistico non dipende dalla natura di queste ultime, siano esse fluttuazioni casuali o dovute a sorgenti esterne. Nel caso più semplice, la sorgente esterna è accoppiata (ovvero influenza il valore) con una singola osservabile (quantità fisica) A del sistema S. La funzione hamiltoniana (in molti casi di interesse essa coincide con l’energia) del sistema perturbato è allora H=H0−AX(t), dove X(t) rappresenta la perturbazione esterna. La risposta del sistema è allora descritta da una funzione a valori complessi α(ω) della frequenza ω della perturbazione, detta suscettività. Essa è determinata dalla relazione 〈A(ω)>=α(ω)X(ω). D’altro canto la funzione di autocorrelazione delle fluttuazioni intorno all’equilibrio risulta essere una funzione a valori reali φ(t) della variabile tempo t. Il teorema afferma allora che la trasformata di Fourier ∼φ(ω) di φ(t) soddisfa la relazione
dove kB è la costante di Boltzmann e T è la temperatura assoluta. Imα(ω) determina quindi la dissipazione di energia come conseguenza di perturbazioni esterne, ovvero come il lavoro fatto sul sistema da una forza esterna è distribuito sui molti gradi di libertà microscopici del sistema.