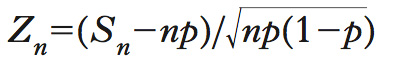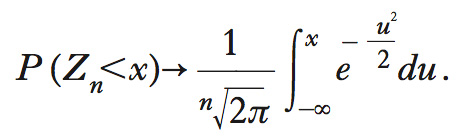limite, teoremi centrali del

limite, teoremi centrali del

Famiglia di teoremi di cruciale importanza nel calcolo delle probabilità e nelle sue applicazioni, che riguarda la convergenza in distribuzione (➔ asintotica, distribuzione) di una successione definita dalla somma di un numero crescente di variabili aleatorie (➔ variabile aleatoria). I teoremi centrali del l. provano che, sotto opportune condizioni, tale successione converge a una variabile aleatoria gaussiana di media zero e varianza unitaria.

Il teorema di De Moivre-Laplace

Dal punto di vista cronologico, il teorema di De Moivre-Laplace può essere considerato il progenitore dei teoremi centrali del limite. Tale teorema risale al 1738, anno di pubblicazione del libro Doctrine des chances di A. De Moivre, e prova la convergenza a una variabile aleatoria normale della successione di variabili aleatorie definita dal conteggio del numero di teste in n lanci di una moneta non necessariamente bilanciata. Sia X_i una variabile aleatoria uguale a 1, se si è osservata testa nell’i-esimo lancio e 0 altrimenti, e sia S_n una variabile aleatoria che indica il numero di teste in n lanci, cioè S_n=X₁+ ... + X_n. Poiché S_n ha distribuzione binomiale (➔ distribuzione di probabilità), con parametri p e n, dove p è la probabilità di ottenere testa in un singolo lancio, si ha E(S_n)=np  e Var (S_n)=np(1−p). Ne segue che la variabile aleatoria

ha media nulla e varianza unitaria. Il teorema di De Moivre-Laplace mostra che la funzione di ripartizione di Z_n è tanto più vicina alla funzione di ripartizione gaussiana standardizzata quanto più n è grande. In formule, per ogni x∈ℜ,

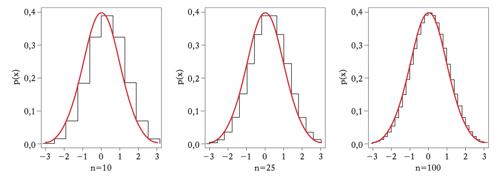
La figura descrive come, all’aumentare del numero di prove, la funzione di probabilità della variabile Z_n tenda ad avvicinarsi sempre più alla curva normale.

Il teorema di Lindeberg-Levy e le sue varianti

La famiglia dei teoremi centrali del l. contiene diverse estensioni del risultato di De Moivre-Laplace. Si consideri, per es., la somma S_n di variabili aleatorie indipendenti e identicamente distribuite, con media μ e varianza σ², entrambe finite, ma con legge arbitraria. Il teorema di Lindeberg-Levy prova che la funzione di ripartizione della variabile aleatoria

Z

_n=(S_n−μ)/σ/√1n

è ben approssimata, per n elevato, dalla distribuzione gaussiana standardizzata. Numerose varianti di tale teorema sono state successivamente dimostrate, estendendo progressivamente il risultato a successioni di variabili aleatorie non identicamente distribuite (teorema di Lyapunov), a vettori aleatori (teorema centrale del l. multivariato), a sequenze di variabili o vettori soggetti a diverse forme di dipendenza e così via.

In econometria e statistica i teoremi centrali del l. sono usati per approssimare la distribuzione campionaria (➔ distribuzione campionaria) di uno stimatore o di una statistica definita come somma di un numero elevato di osservazioni.