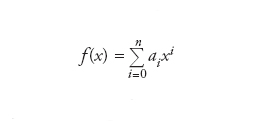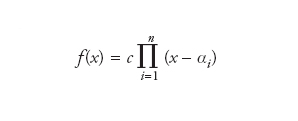teorema fondamentale dell'algebra
teorema fondamentale dell’algebra
Teorema che stabilisce, per ogni polinomio a coefficienti complessi, l’esistenza di almeno una radice nel campo dei numeri complessi. Più precisamente, per ogni polinomio
con ai∈ℂ e an≠0 (n è detto grado del polinomio) esiste un x0∈ℂ tale che f(x0)=0. Individuata una radice (complessa), non è poi difficile dimostrare che ogni polinomio può essere decomposto nel prodotto di termini lineari (di grado 1), ovvero
con c,αi∈ℂ. I numeri complessi αi sono evidentemente radici del polinomio e anche se può verificarsi il caso αi=αj con i≠j, è chiaro cosa si intenda quando si afferma che, tenendo conto di eventuali molteplicità, un polinomio a coefficienti complessi ha sempre un numero di radici complesse pari al suo grado. È questa la forma completa del teorema fondamentale dell’algebra. Il teorema è stato per la prima volta enunciato da René Descartes nel 1637, seppure in veste diversa da quella oggi adottata. Sono stati Colin MacLaurin e Leonhard Euler a rendere la formulazione più precisa e sostanzialmente equivalente a quella contemporanea. Una dimostrazione vera e propria è stata data per la prima volta da Jean d’Alembert nel 1746; altre ne seguirono per mano di Euler, Pierre-Simon de Laplace, Joseph-Louis Lagrange tra gli altri. L’elemento che tutte queste avevano in comune era l’assunzione iniziale che radici con particolare caratteristiche esistessero effettivamente; solo in un secondo momento era provato che si trattava di numeri complessi (che includono, lo ricordiamo, i numeri reali). Fu Carl Friedrich Gauss il primo a dimostrare il teorema fondamentale dell’algebra senza assumere in alcun modo l’esistenza di radici. Da allora sono stati forniti numerosi nuovi argomenti, ma tutti fanno uso in qualche forma delle proprietà topologiche dei numeri reali o complessi. Il ruolo di queste proprietà è stato alla fine ridotto alla dimostrazione che un polinomio a coefficienti reali di grado dispari ha almeno una radice.
→ Algebra