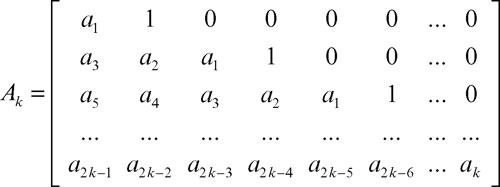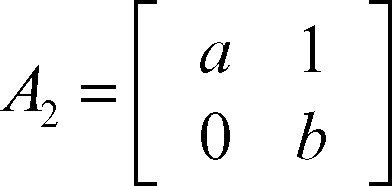Routh-Hurwitz, teorema di
Routh-Hurwitz, teorema di
Routh-Hurwitz, teorema di generalizzazione della regola di → Cartesio, che consente di stabilire quante delle radici di un polinomio hanno parte reale positiva o negativa. Più precisamente, il teorema stabilisce che le radici di un polinomio monico a coefficienti reali p(x) = xn + a1xn−1 + ... + an hanno tutte parti reali negative se i determinanti Δ1, ..., Δn, sono tutti positivi, dove Δk è il determinante della matrice quadrata di dimensione k × k
nella quale si pone ai = 0 se i > n. Per esempio, nel caso di un polinomio di secondo grado x 2 + ax + b, si ha A1 = [a] e
e pertanto la condizione espressa dal teorema equivale in questo caso a richiedere che a e b siano entrambi positivi o entrambi negativi. Il teorema consente di discutere in modo puramente algoritmico, e senza determinarne le soluzioni, la stabilità di un sistema differenziale a coefficienti costanti.