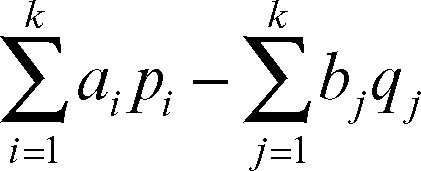Riemann-Roch, teorema di
Riemann-Roch, teorema di
Riemann-Roch, teorema di in geometria, fornisce una stima, e in molti casi il numero esatto, della dimensione dello spazio vettoriale delle funzioni meromorfe definite su una data superficie di Riemann compatta aventi un preassegnato comportamento polare. Un divisore D di una superficie di Riemann compatta S è un insieme finito P = {p1, ..., pk} di punti di S (senza ripetizioni nell’elenco) con un’applicazione P → Z0 che a ogni punto pi di P associa un intero non nullo ai. D è quindi una combinazione formale finita a coefficienti interi e non nulli di punti di P.
È possibile che l’applicazione sia vuota e, in tal caso, il divisore è detto nullo e si indica con 0. Si indica con deg(D) il grado del divisore, cioè la somma (finita) dei coefficienti numerici che compaiono nell’espressione precedente. Ogni D può essere scritto in modo unico come differenza di due divisori nel seguente modo:
Si indica con L(D) lo spazio vettoriale complesso i cui elementi sono le funzioni meromorfe su S che sono olomorfe in SP, che hanno nei punti pi un polo di molteplicità minore di o uguale ad ai e che hanno nei punti qj degli zeri di ordine almeno uguale a bj. Si indica poi in modo analogo con I(D) uno spazio differenziale meromorfo con preassegnati zeri e preassegnati comportamenti polari. Il teorema di Riemann-Roch stabilisce che se X è una superficie di Riemann compatta di genere g, D un divisore di X e gli spazi L(D) e I(D) sono di rispettiva dimensione finita l(D) e i (D), allora vale la relazione:
in cui deg(D) è il grado del divisore.