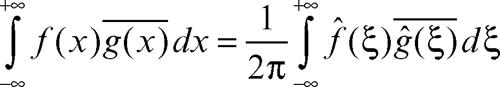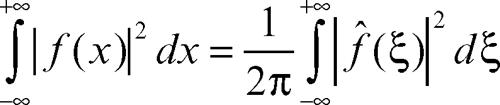Plancherel, teorema di
Enciclopedia della Matematica (2013)
Plancherel, teorema di
Plancherel, teorema di identifica una delle proprietà della trasformata di Fourier:
dove il segno di circonflesso indica appunto la trasformazione di Fourier. Il teorema è valido se le due funzioni ƒ e g ∈ L2(R) e mostra che la trasformata di Fourier (a meno del fattore 1/(2π) che si può evitare con una differente definizione) è una isometria di L2(R) su sé stesso (→ spazio Lp(Ω)). Come caso particolare si ottiene: