Pitagora, teorema di
Pitagora, teorema di
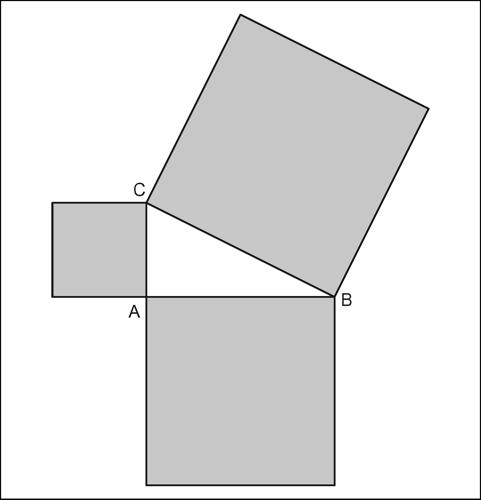
Pitagora, teorema di teorema fondamentale della geometria euclidea del piano. Esso stabilisce che in un qualsiasi triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti. In un triangolo rettangolo ABC con angolo retto in A si ha perciò:
Vale anche il teorema inverso: se in un triangolo la somma delle aree dei quadrati costruiti su due suoi lati è uguale all’area del quadrato costruito sul terzo lato, allora il triangolo è rettangolo. Il teorema di Pitagora, nella geometria euclidea del piano, è particolarmente importante sia da un punto di vista applicativo (perché fornisce le condizioni che assicurano la perpendicolarità di due linee, fondamentale in tutte le tecniche costruttive) sia da un punto di vista teorico (perché, insieme ad altri teoremi di equivalenza nel piano, assicura che il quadrato possa essere assunto come figura base delle superfici e dunque permette di fissare una unità di misura per le superfici stesse: il metro quadrato).
Indicando con a, b, c, rispettivamente, la misura dell’ipotenusa e le misure dei due cateti di un triangolo rettangolo, il teorema di Pitagora stabilisce che a2 = b2 + c2. Da ciò segue che, noti due dei tre lati, è possibile ricavare il terzo. Il teorema di → Carnot o teorema del coseno, estende il teorema di Pitagora a triangoli qualunque (non soltanto rettangoli). Esso afferma che se a, b, c sono lati di un triangolo e α l’angolo compreso tra i lati b e c, vale la relazione a2 = b2 + c2 − 2bccosα. Il teorema di Pitagora è un caso particolare del teorema di Carnot per α = 90° (cosα = 0).
La distanza tra due punti P(xP, yP) e Q(xQ, yQ) di un piano cartesiano, detta anche distanza pitagorica, viene calcolata utilizzando il teorema di Pitagora mediante la formula
Analogamente, nell’ordinario spazio tridimensionale in cui sia definito un riferimento cartesiano Oxyz, la distanza tra due punti P(xP, yP, zP) e Q(xQ, yQ, zQ) è data da