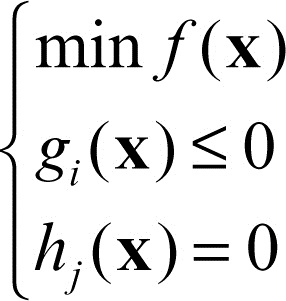Kuhn-Tucker, teorema di
Kuhn-Tucker, teorema di
Kuhn-Tucker, teorema di conosciuto anche come condizioni di Karush-Kuhn-Tucker o condizioni kkt, stabilisce condizioni necessarie affinché un problema di programmazione non lineare, i cui vincoli soddisfino delle date condizioni di regolarità, abbia soluzione. Sia il problema formulato dal seguente sistema di formule, nel quale: nella prima formula compare la funzione obiettivo f(x): Rn → R da rendere minima; nelle altre due formule, in cui i = 1, …, m e j = 1, …, n, compaiono rispettivamente i vincoli di disuguaglianza e i vincoli di uguaglianza
con gi (x): Rn → R e hj (x): Rn → R.
Siano ƒ(x), gi (x) e hj (x) continuamente differenziabili nell’intorno del punto x0 di minimo e soddisfacenti in esso le condizioni di regolarità dei vincoli; allora esistono moltiplicatori μj e λi tali che:
• gi (x0) ≤ 0 per ogni i = 1, …, m
• hj( x0) = 0 per ogni j = 1, …, n
• λi ≥ 0 con i = 1, …, m
• λigi (x0) = 0 per ogni i = 1, …, m
dove con ∇ si è indicato il gradiente.
Questo sistema di formule è indicato come condizioni di Karush-Kuhn-Tucker (kkt). La regolarità richiesta per i vincoli in x0 è espressa da un insieme di condizioni sintetizzabili nel fatto che x0 sia un punto regolare (→ superficie). Le condizioni kkt estendono il metodo dei moltiplicatori di → Lagrange.