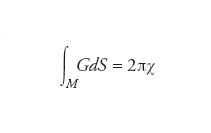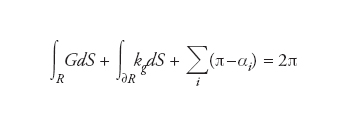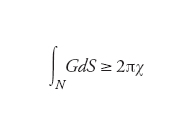teorema di Gauss-Bonnet
teorema di Gauss-Bonnet
Importante teorema della geometria differenziale, secondo il quale la caratteristica di Euler χ di una varietà compatta bidimensionale M è legata all’integrale della curvatura di Gauss (totale) G dalla
La caratteristica di Euler di M è data dalla formula χ=V−E+F per una divisione di M in poligoni dotati di un numero V di vertici, E di spigoli e F di facce. Per es., dividendo una superficie sferica di raggio unitario S2 in quattro ‘spicchi’ si ottiene χ=2−4+4=2 mentre nel caso di un cubo otteniamo χ=8−12+6. Segue dal teorema di Gauss-Bonnet che la caratteristica di Euler è indipendente dalla scelta della divisione di M ed è dunque un invariante topologico. Non a caso, per una superficie di genere g (ossia una superficie S2 ottenuta incollando su di essa un numero g≥0 di manici) si ha χ=2−2g. Nella sua forma locale, il teorema di Gauss-Bonnet per una qualunque sottosuperficie R di M è espresso dalla
dove kg è la curvatura geodetica della curva regolare a tratti ∂R (il bordo della superficie R) e la somma è su tutti gli angoli interni αi degli angoli (i punti in cui ∂R non è regolare) della stessa ∂R. Nel caso di varietà riemanniane bidimensionali non compatte senza bordo N2, è valido un analogo risultato, noto come disuguaglianza di Cohn-Vossen:
Il teorema di Gauss-Bonnet ammette infine una generalizzazione al caso di varietà riemanniane regolari e compatte di dimensione pari 2d, detto teorema di Gauss-Bonnet-Chern. Quest’ultimo è una conseguenza del teorema dell’indice di Atiya-Singer.