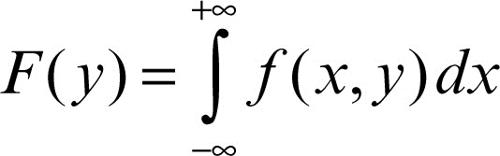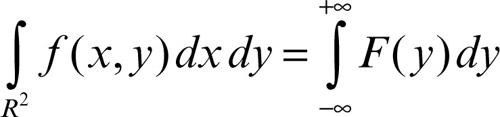Fubini, teorema di

Fubini, teorema di

Fubini, teorema di in analisi, stabilisce che se ƒ(x, y) è una funzione sommabile di due variabili, allora:

• per quasi ogni y la funzione ƒ(x, y) è sommabile rispetto a x;

• l’integrale

è finito per quasi ogni y ed è una funzione sommabile in y;

• vale la formula

Il teorema vale anche per funzioni definite in un sottoinsieme E misurabile di R², estendendole con la posizione ƒ(x, y) = 0 per (x, y) ∉ E. Il teorema si generalizza al caso di funzioni con un numero qualsiasi di variabili ƒ: R^n+m → R, consentendo la riduzione di un integrale multiplo (n + m)-dimensionale a due successivi integrali n- e m-dimensionali.