Desargues, teorema di
Desargues, teorema di
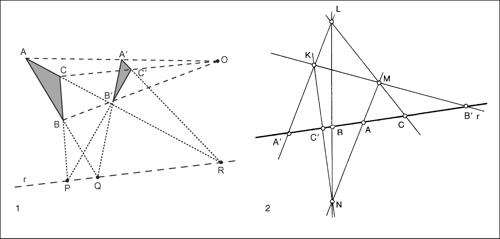
Desargues, teorema di o teorema dei triangoli omologici, in geometria proiettiva, stabilisce che se due triangoli ABC e A′B′C′ senza vertici in comune sono tali che le coppie di vertici omologhi sono tutte allineate con uno stesso punto O (proprio o improprio), allora le coppie di rette AB e A′B′, BC e B′C′, AC e A′C′ si intersecano in tre punti allineati, e viceversa. In altri termini, esso stabilisce che due triangoli sono in prospettiva rispetto a un punto se e solo se sono in prospettiva anche rispetto a una retta.
Il teorema di Desargues è autoduale, cioè coincide con il suo duale, ottenuto scambiando tra loro i termini retta e punto (→ dualità). Il teorema, pur non riguardando questioni metriche, è ricavabile per via algebrica nel piano euclideo, una volta definito un sistema di riferimento cartesiano, ma non è deducibile dagli assiomi di piano affine. Si possono pertanto costruire geometrie in cui esso non è valido (geometrie non desarguesiane) e geometrie nelle quali si assume esso o un suo equivalente come ulteriore assioma (geometrie desarguesiane).
☐ Un secondo teorema di Desargues stabilisce che le coniche di un fascio (comprese le tre degeneri, costituenti un quadrangolo completo) tagliano sopra una retta non passante per i punti base del quadrangolo (i vertici) coppie di punti di una involuzione.
Sempre come teorema di Desargues è riportato in letteratura il teorema del quadrangolo completo, in realtà già presente nelle Collectiones mathematicae di Pappo: tagliando le tre coppie di lati opposti di un quadrangolo completo con una retta non passante per alcuno dei vertici si ottengono tre coppie di punti coniugati in una stessa involuzione.