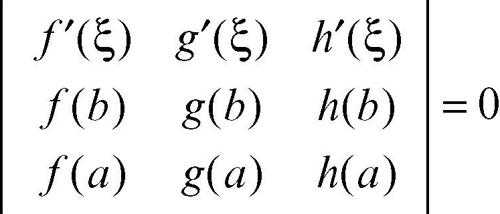Cauchy, teorema di

Cauchy, teorema di

Cauchy, teorema di o teorema degli incrementi finiti, generalizzazione del più noto teorema di → Lagrange, utile in alcune dimostrazioni dell’analisi (per esempio, nella dimostrazione del teorema di de → L’Hôpital). Date due funzioni ƒ(x) e g(x), continue nello stesso intervallo chiuso e limitato [a, b], derivabili nel corrispondente intervallo aperto (a, b), il teorema di Cauchy afferma che esiste un punto ξ ∈ (a, b) tale che

Se si aggiunge l’ipotesi che ∀x, g′ (x) ≠ 0, si può scrivere questo risultato nella forma più significativa

Il teorema di Lagrange risulta così essere un caso particolare di questo teorema relativo al caso in cui g(x) = x. A sua volta il teorema di Cauchy è il caso particolare, corrispondente a h(x) ≡ 1, del seguente teorema: date tre funzioni ƒ(x), g(x) e h(x), continue nello stesso intervallo chiuso e limitato [a, b] e derivabili nel corrispondente intervallo aperto (a, b), esiste un punto ξ ∈ (a, b) tale che