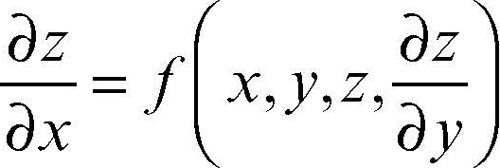Cauchy-Kovaleskaja, teorema di
Enciclopedia della Matematica (2013)
Cauchy-Kovaleskaja, teorema di
Cauchy-Kovaleskaja, teorema di in analisi, stabilisce che l’equazione differenziale alle derivate parziali
dove ƒ è una funzione analitica in (x0, y0, z0, (∂z/∂y)0), ha esattamente una soluzione z(x, y) che è analitica in (x0, y0) e per la quale z(x0, y) = g(y) definisce una funzione g tale che g(y0) = z0 e g ′(y0) = (∂z/∂y)0. Tale proprietà può essere generalizzata a funzioni di più variabili indipendenti, a derivate di ordine superiore e a sistemi di equazioni differenziali.