verita, tavola di

Enciclopedia della Matematica (2013)

verita, tavola di


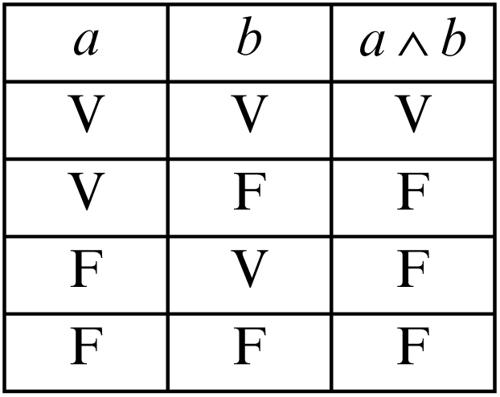
verità, tavola di metodo semantico della logica proposizionale (→ enunciati, linguaggio degli) per determinare il valore di verità («vero» V oppure «falso» F) di un enunciato composto in funzione dei valori di verità degli enunciati elementari (o atomici) che ne sono i costituenti. Per esempio, se le lettere a e b indicano due enunciati elementari, che possono essere veri o falsi, l’enunciato composto a ∧ b, ottenuto con la loro congiunzione è vero se e solo se sia a sia b sono veri. La corrispondente tavola di verità è la seguente:

table

Nel caso della logica classica (ma la considerazione risulta valida anche in molti altri sistemi di logica) il metodo delle tavole di verità è un metodo di decisione, nel senso che consente di determinare, in un numero finito di passi, se un enunciato è valido, cioè vero per qualsiasi interpretazione.

Ciò avviene nel linguaggio degli enunciati nel caso di → tautologie; simmetricamente, un enunciato che è falso, indipendentemente dai valori di verità dei suoi costituenti, è una → contraddizione e risulterà falso in ogni interpretazione.

Le tavole di verità risalgono alla logica stoica e megarica, ma la loro prima esplicita descrizione ed elaborazione è opera di Ch.S. Peirce (1880); esse sono poi state estensivamente riprese, intorno al 1920, da J. Łukasiewicz, E.L. Post e L. Wittgenstein.

A ogni connettivo è associata univocamente la sua tavola di verità ed è possibile così utilizzare questa rappresentazione per calcolare algoritmicamente il valore di verità di un enunciato composto. Per esempio, la tavola di verità dell’enunciato (tautologia)

formula

è la seguente:

table

Vedi anche
NAND In elettronica e informatica, denominazione internazionale, composta dalla N di NOT e da AND, dell’operazione di inversione (o negazione) del prodotto logico AND tra variabili booleane, della funzione corrispondente, e anche del circuito che la realizza. Come avviene per l’altra funzione logica universale ... implicazione Geologia In petrografia, si chiama struttura di i. quella di una roccia caratterizzata da interpenetrazione di due minerali prevalenti, in modo che un fascio di individui dell’uno, disposti più o meno parallelamente, traversa un individuo o un fascio di individui dell’altro, anch’essi grossolanamente ... pòrta lògica Circuito elettronico al quale è demandato il compito di eseguire operazioni elementari dell'algebra booleana (NOT, AND, OR ecc.) all'interno di circuiti più complessi. Le p.l. sono le unità fondamentali dei circuiti integrati e sono classificate in funzione del tipo di semiconduttore utilizzato per la ... contraddizione Come termine specifico di logica, la c. è il rapporto vigente tra un’affermazione e una negazione di egual soggetto e di egual predicato. In questa antitesi, vero essendo un termine, l’altro deve essere falso ( principio di c.). La prima rigorosa formulazione del principio di c. s’incontra in Aristotele, ...
Tag
Vocabolario
tàvola
tavola tàvola s. f. [lat. tabŭla]. – 1. Asse di legno di spessore sensibilmente minore della lunghezza e della larghezza: segare, piallare una t.; accatastare le t.; chiudere un’apertura con tre t. inchiodate; t. di salvezza, quella a cui...
verità
verita verità s. f. [lat. vērĭtas -atis, der. di verus «vero»]. – 1. Carattere di ciò che è vero, conformità o coerenza a principî dati o a una realtà obiettiva: dubitare della v. di una notizia; non credere alla v. delle parole di qualcuno;...