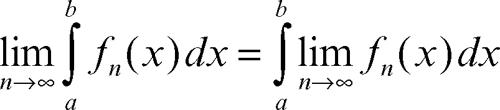successione di funzioni
successione di funzioni
successione di funzioni successione {ƒn(x)} i cui termini sono funzioni. Per ogni x dell’insieme di definizione comune a tutte le funzioni, una successione di funzioni è una → successione numerica. Si dice che {ƒn(x)} converge in x0 se la successione numerica {ƒn(x0)} converge; che {ƒn(x)} converge puntualmente in un insieme E, contenuto nell’insieme di definizione comune, se converge in ogni x ∈ E. Si dice infine che {ƒn(x)} converge uniformemente a ƒ(x) in E′ ⊆ E se
Se le funzioni ƒn(x) sono continue, e la successione converge uniformemente, anche la funzione limite ƒ(x) è continua. Se invece la successione converge solo puntualmente, è possibile che ƒ(x) sia discontinua. Per esempio, la successione {(2/π)arctan(nx)} converge in R alla funzione ƒ(x) = sgn(x). Se le funzioni ƒn(x) sono derivabili, si può considerare la successione derivata, i cui elementi sono le derivate degli elementi della successione data. La derivabilità della funzione limite ƒ(x) è assicurata dall’ipotesi di uniforme convergenza della successione delle derivate {ƒ′n(x)}, altrimenti può venire a mancare: per esempio la successione
converge uniformemente alla funzione continua |x|, che tuttavia non è derivabile nell’origine.
La nozione di convergenza uniforme è importante nel passare al limite sotto il segno d’integrale: questo è infatti lecito sotto l’ipotesi di convergenza uniforme della successione integranda; in formula, se ƒn converge uniformemente in [a, b] allora
Queste definizioni e proprietà si estendono a funzioni di più variabili.