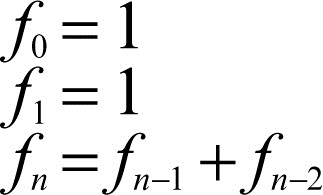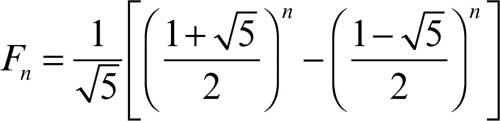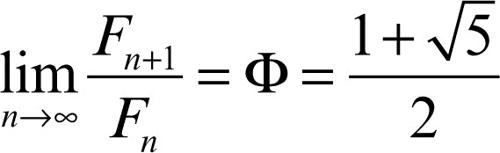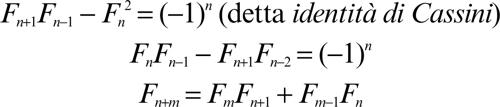Fibonacci, successione di

Fibonacci, successione di

Fibonacci, successione di successione di numeri naturali; prende il nome dal matematico pisano L. Fibonacci, che la introdusse nel suo Liber abaci, ed è indicata anche, sebbene impropriamente, come serie di Fibonacci. Fibonacci la introdusse per dare una descrizione regolare e numerica della crescita mensile di una popolazione di conigli, supponendo che essi diventino fertili al compimento del primo mese e ogni coppia di conigli partorisca al compimento del secondo mese. Così, i primi due termini della successione sono entrambi uguali a 1, mentre ciascun termine dal terzo in poi è uguale alla somma dei due che lo precedono. La successione {ƒ_n} è, quindi, così definibile ricorsivamente (→ ricorsività):

I termini della successione sono detti numeri di Fibonacci e i primi 25 di essi sono: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233, 377, 610, 987,1597, 2584, 4181, 6765,10946, 17711, 28657, 46368, 75025.

La successione di Fibonacci è da sempre circondata da un’aura di mistero e ha sempre esercitato un grande fascino in ambiti anche distanti dalla matematica poiché si presta a descrivere alcune regolarità osservabili in fenomeni naturali di crescita. Per questo, anche se alcuni riferimenti a essa sono piuttosto forzati, i suoi termini si utilizzano in modellizzazioni matematiche di fenomeni di vario tipo, dalla disposizione delle foglie lungo un ramo di una pianta in crescita ai fenomeni acustici e di riconoscimento di onde sonore. Per esempio, nel regno vegetale una sequenza di numeri di Fibonacci sembra trovarsi nella distribuzione a spirale dei flosculi delle margherite e dei semi di girasole. In entrambi i casi, vi sono due insiemi di spirali logaritmiche, una avvolta in senso orario e una in senso antiorario. I numeri delle spirali non sono uguali nei due sensi, ma tendono a essere due numeri di Fibonacci consecutivi (in genere 21 e 34 nelle margherite, 34 e 55 nei girasoli medi). Analoghe serie di spirali si trovano nelle pigne (5 e 8), negli ananas (8 e 13) e in molte piante le cui foglie crescono a spirale.

Nella trattazione più formale si aggiunge il numero 0 come numero di posto 0 nella successione, contrariamente a quanto storicamente proposto dal suo ideatore. Il termine di posto 1, indicato con F₁ è 1, così come il termine F₂; ogni altro termine è individuato applicando la regola ricorsiva. Si definisce così la successione di Fibonacci come la successione di naturali formata dalla soluzione della equazione alle differenze F_n+2 = F_n+1 + F_n, a partire dai dati iniziali F₀ = 0, F₁ = 1. L’espressione generale del termine di posto n è

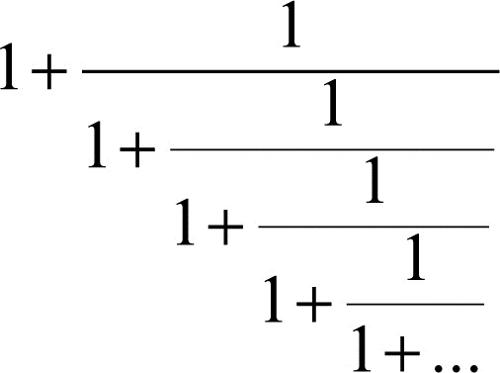
Il quoziente di due numeri di Fibonacci consecutivi è una ridotta della frazione continua

e tende al → numero aureo:

caratteristica questa che accresce la suggestione esercitata da questa successione numerica in quanto il rapporto aureo era assunto nell’arte classica come canone di perfezione.

Altre interessanti relazioni che coinvolgono i numeri di Fibonacci sono:

Il massimo comune divisore di due numeri di Fibonacci è anch’esso un numero di Fibonacci e si ha mcd(F_m, F_n) = F_{MCD(m, n)}, da cui si ricava che il numero di Fibonacci F_n è divisibile per il numero di Fibonacci F_m se e solo se n è divisibile per m. Inoltre, ogni numero di Fibonacci può essere ottenuto come somma dei numeri di Fibonacci che lo precedono tranne il suo immediato predecessore, aumentata di 1:

Anche i quadrati dei numeri di Fibonacci presentano caratteristiche interessanti. Moltiplicando un numero della successione per sé stesso e sommando i risultati ottenuti si ottiene un’altra successione

nella quale la somma di tutti i quadrati fino all’n-esimo termine della successione è equivalente al prodotto dell’n-esimo numero di Fibonacci per il successivo:

Legato ai numeri di Fibonacci è un procedimento numerico per la determinazione del punto di minimo, x₀, di una funzione unimodale in un intervallo [a, b], ossia avente un solo punto di minimo nell’intervallo, e inoltre tale che ƒ(x) > ƒ(x′ ) per ogni scelta dei punti x e x′ per cui x < x′ < x₀ oppure x > x′ > x₀. Tale metodo consiste nella determinazione di due punti interni

dove n è il numero massimo di valutazioni della funzione che si è disposti a effettuare, e nel successivo calcolo dei valori della funzione in corrispondenza di essi; in base al confronto di tali valori, è possibile limitarsi a effettuare la successiva ricerca in uno solo dei due intervalli [a, b₁] e [a₁, b], in corrispondenza del quale viene ripetuto lo stesso procedimento. La scelta dei punti così effettuata consente, nelle successive applicazioni dell’algoritmo, di calcolare a ogni passo un solo nuovo valore della funzione, essendo l’altro già stato calcolato nel passo precedente. Questo procedimento, tra tutti quelli basati sul calcolo di n valori della funzione, è quello che fornisce la massima riduzione (pari a 1/F_n) dell’intervallo iniziale di incertezza.