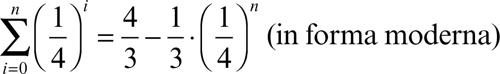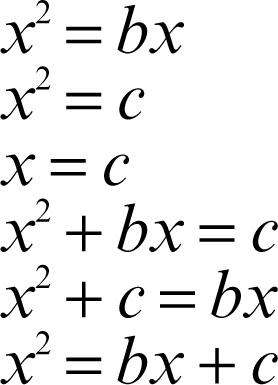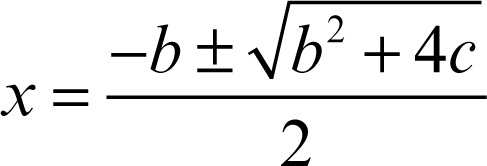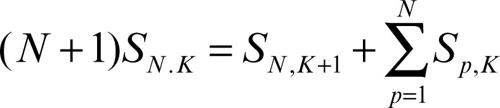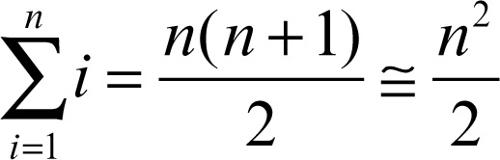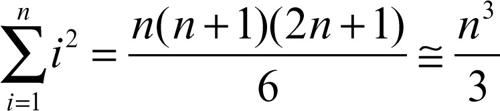STORIA DELLA MATEMATICA

STORIA DELLA MATEMATICA

STORIA DELLA MATEMATICA

Il tempo della scienza senza tempo

La matematica è la più antica e la più immutabile delle discipline. Si può dire che la matematica di base, quella insegnata oggi nella scuola primaria, è pressoché identica in tutte le scuole del mondo, da New York ai villaggi africani, e non è molto diversa da quella che insegnavano gli scribi babilonesi o egiziani.

La matematica è nata in Oriente e persino il linguaggio matematico rivela le influenze islamiche (algebra e algoritmo sono, per esempio, termini di origine araba); di origine indiana è anche la moderna notazione numerica. Tutta l’area dall’India al Mediterraneo è stata per millenni percorsa da vie commerciali e interessata da scambi culturali, influenze religiose e massicce migrazioni di popoli.

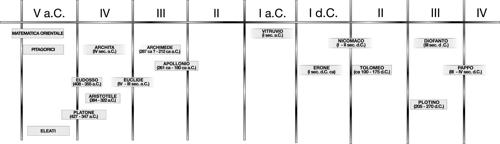
La scienza e la matematica moderna sono nate nel Seicento e da allora si sono sviluppate in maniera costante, plasmando il mondo così come lo conosciamo. Usualmente se ne pongono le basi nella matematica greca del periodo aureo, fiorita nei secc. iv e iii a.C. tra l’Accademia platonica di Atene e il Museo e la Biblioteca di Alessandria d’Egitto. Nei quasi duemila anni che separano queste due fasi storiche molti dei testi originali sono andati distrutti o perduti. I codici più antichi degli Elementi di Euclide sono di oltre mille anni successivi all’originale, un millennio di copie e traduzioni da cui il testo non è rimasto indenne. Anche peggiore la sorte toccata alle opere di Archimede e Apollonio. Scomparsi i testi, chiuse scuole e istituzioni culturali, svanita ogni testimonianza e memoria, nel medioevo si dissolve la continuità della tradizione matematica, al punto che oggi è problematico ricostruire il senso stesso dei termini antichi. Può venire addirittura il sospetto che la scienza moderna sia in realtà erede degli artigiani fiorentini e degli scolastici parigini più che dei matematici greci di Alessandria.

Oggi la matematica presenta un quadro unitario a livello internazionale ed è priva di differenze geografiche, ma nel passato sono esistite tradizioni matematiche autonome: la matematica cinese, per esempio, è cresciuta autonomamente per duemila anni, ed è giunta a livelli fino a cinque secoli fa paragonabili se non superiori a quelli della coeva matematica europea. Nel confronto, appaiono peculiarità distinte, che riflettono i caratteri profondi delle due culture, ma si notano anche indubbie somiglianze: i numeri sono sostanzialmente gli stessi e solo la notazione appare diversa; le operazioni su di essi sono affini, le figure geometriche fondamentali sono le stesse, e i calcoli pure.

Gli Elementi di Euclide sono il più importante libro scientifico di tutti i tempi e fino a quattro secoli fa erano ancora la base di tutto il sapere scientifico e il paradigma dell’idea stessa di razionalità. Ancora oggi potrebbero essere usati come libro di testo nelle scuole superiori quasi senza modifiche. Così, la matematica sembra avere uno sviluppo lineare, sembra crescere su sé stessa, senza mai rinnegare il suo passato, senza rivoluzioni, senza tempo. Di qui l’idea diffusa che la matematica sia solo la scoperta progressiva di un «mondo di idee», un regno immateriale ma tuttavia reale quanto quello fisico che ci circonda. Secondo tale diffusa idea la storia della matematica si configura come la storia della scoperta progressiva di questo mondo.

In tempi più recenti si è considerata la matematica come il linguaggio di una scienza essenzialmente empirica. In tale visione, la matematica è solo uno strumento linguistico. Conseguentemente, la sua storia appare lineare, in un certo senso dipendente dalle storie delle altre scienze (della fisica, della tecnica, della filosofia) in quanto storia di uno strumento che si adegua alle esigenze di altre discipline, anziché un settore di studi dal cui interno scaturiscono teorie e concetti autonomi. E ancora una volta, così intesa, la matematica risulta uno strumento monotono nella sua prevedibilità, appare ovvia, logica, “naturale”, e forse anche un po’ noiosa. In ogni caso finisce con l’essere la parte più prettamente formale di una storia della scienza che nel secolo scorso è stata vista come “storia delle idee”.

In verità, la storia della matematica è segnata da svolte radicali, da fratture capaci di fondare una nuova concezione del mondo. Fratture che anche oggi uno studente avverte quando passa per esempio dallo studio dell’aritmetica e della geometria a una matematica intessuta di simboli algebrici e concetti più astratti quale per esempio quello di funzione. Le idee matematiche si mostrano talvolta come creazioni inaudite basate su apparenti assurdità. Per i greci lo zero non esisteva e l’uno non era un numero. Fino al medioevo il concetto di numero reale era sconosciuto; lo intuirono gli arabi, e infine nel Seicento esso fu introdotto, pur tra le difficoltà concettuali che esso comportava soprattutto in relazione alla sua rappresentazione decimale infinita e alla definizione di continuità a esso correlata. I numeri reali furono infine accettati divenendo strumenti di lavoro indispensabili, tanto da apparire ben presto quasi una ovvietà, ma dovettero trascorrere ancora due secoli perché ricevessero una formulazione scientifica con G. Cantor e R. Dedekind, che elaborarono una rigorosa costruzione dell’insieme R dei numeri reali a partire dall’insieme Q dei numeri razionali.

La storia della matematica è dunque una storia del tutto anarchica e irrazionale, costellata di percezioni geniali e di intuizioni improvvise? Oppure al di sotto delle idee logiche e razionali alternate ai concetti più astrusi si possono intuire i tratti di un’unica storia cognitiva, complessa e sfaccettata?

Certamente, la matematica parla dei caratteri fondamentali della realtà a un livello che sembra trascendere la storia e la geografia antropiche. Ma nel contempo essa permea l’insediamento umano nel mondo, rispecchiando le manifestazioni antropologiche e culturali delle diverse civiltà, dalla religione all’arte, dalla musica al linguaggio. Ma soprattutto rivela i caratteri più profondi e nascosti del rapporto cognitivo tra l’uomo e ciò che lo circonda.

La matematica antica

La matematica viene dall’Oriente e fino a quasi tutto il medioevo è sempre stata un prodotto orientale: la Grecia antica si può considerare la periferia dell’Oriente. Archimede di Siracusa (287?-212 a.C.) è il più “occidentale” matematico antico, ma i suoi riferimenti culturali erano tutti orientali. Si può considerare Leonardo da Pisa, detto Fibonacci, vissuto nella prima metà del xiii secolo, il primo matematico “occidentale”.

Prima dei greci la matematica era patrimonio degli scribi, sacerdoti del tempio e del palazzo che avevano il monopolio della cultura, della scrittura e della matematica. Quest’ultima, pur presente negli antichi miti e rituali, aveva un ruolo essenzialmente pratico: calcoli relativi ad aree, a quantità di beni, a problemi amministrativi. Harpenodaptai (tenditori di corde) erano detti gli scribi egizi che dopo ogni inondazione del Nilo rimisuravano con corde e paletti i campi per ridisegnarne i confini.

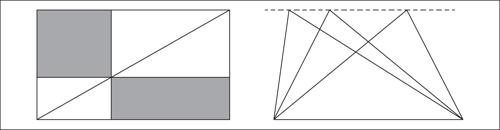
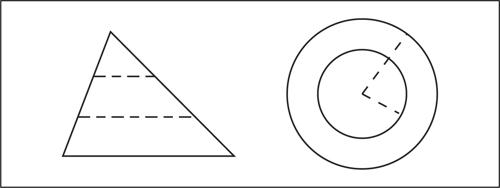
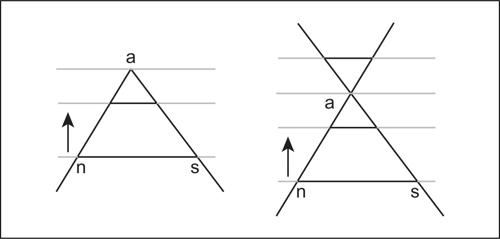
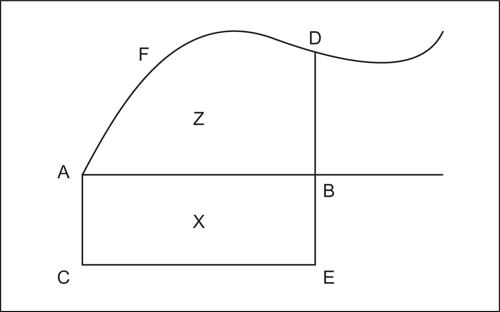
Probabilmente la matematica si svolgeva soprattutto sull’abaco, che all’origine era solo una superficie piana coperta di sabbia sulla quale si potevano tracciare linee e poggiare sassolini (calculi, in latino). Era l’antenato del moderno pallottoliere, ma serviva probabilmente anche a realizzare costruzioni geometriche e calcolare le aree delle figure (la fig. 1 mostra come si poteva scoprire sull’abaco la regola per il calcolo dell’area del rettangolo).

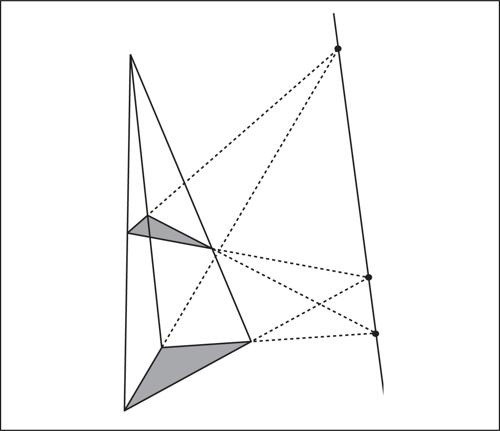
Del resto, è noto l’aneddoto plutarchiano in cui si narra che lo stesso Archimede fu ucciso sulla spiaggia mentre era impegnato in una dimostrazione geometrica tracciata sulla sabbia. I sassolini finivano con l’essere nel contempo punti, quadratini unitari e unità, antenati di quelle che i greci chiameranno monadi, così che tanto un intervallo di lunghezza n quanto il numero intero n saranno da essi considerati una sequenza lineare di n unità (fig. 2).

Nella matematica antica, legata a problemi concreti (di agrimensura, di registrazione dei beni ecc.), non si trova traccia di dimostrazioni, ma questa assenza non deve indurre a ritenere la matematica antica una scienza poco elaborata. Per esempio, gli egizi possedevano un algoritmo per la moltiplicazione tra interi, che usava non le tabelline ma la scrittura binaria dei numeri, e che così si può descrivere: si supponga, per esempio, di voler moltiplicare 27 per 13. Si raddoppi il numero 27 e si ripeta la moltiplicazione per 2 fino a ottenere il multiplo di 27 secondo il fattore 2ⁿ (cioè 2ⁿ ⋅ 27), la massima tra le potenze di 2 minore di 13 (e quindi n = 3, perché 2³ = 8 < 13, mentre 2⁴ = 16 > 13), e si scriva 13 come somma di multipli di 2 fino a tale massima potenza di 2: si ottiene 13 = 8 + 4 + 1. Si contrassegnino ora con una × soltanto i multipli di 2 che compaiono in tale somma e, nella terza riga della seguente tabella, si considerino i multipli di 27 secondo i corrispondenti fattori che compaiono nella seconda riga (che possono essere semplicemente ottenuti, a partire da 27, per raddoppiamenti successivi: 27, 54, 108 ecc.):

Infine, si sommino i multipli contrassegnati dalla × che compaiono nella terza riga; si ottiene: 216 + 108 + 27 = 351, che è il risultato cercato, cui si è giunti senza far ricorso a tabelline.

La tradizione pratica

La matematica pregreca, per il suo carattere pratico, si configurava essenzialmente come un insieme di tecniche di calcolo. Pur derivando da questa matematica pratica, la geometria teorica greca se ne distaccherà nettamente, al punto che dal v sec. a.C. fino al xvi sec. d.C. si possono riconoscere nella matematica due tradizioni nettamente distinte, una pratica e una teorica.

La tradizione pratica, che resterà viva fino al rinascimento, può essere definita una matematica dell’abaco, meno ricca di implicazioni teoriche rispetto alla grande geometria greca classica, ma tuttavia diffusa in tutto il Mediterraneo e nel Medio Oriente. È la tradizione sviluppatasi sin dal iii millennio a.C. in Mesopotamia, presente nella matematica egiziana, indiana ed ellenistica, fino a Erone e Diofanto. Era la matematica del contingente, delle applicazioni, delle professioni (amministratori e agrimensori, architetti e tecnici, artigiani e mercanti). Si tramandava soprattutto oralmente e per apprendistato (la scrittura era usata solo per elenchi di problemi e tavole numeriche), e, diversamente dalla tradizione teorica, era attenta al dato numerico empirico e alla misurazione. Il radicamento nelle applicazioni pratiche le permise di sopravvivere anche al crollo dell’impero romano d’Occidente, e di rifiorire nel medioevo tanto nel mondo islamico quanto in Europa.

Una tale matematica impermeabile alle questioni della geometria teorica, allo stile assiomatico-deduttivo e alla distinzione discreto/continuo, nella quale le tecniche erano esplicitamente aritmetiche, la geometria era sempre e solo metrica e descrittiva e non vi era una differenziazione tra unità e punto (se non nel fatto che il punto “aveva una posizione”), era in termini cognitivi una aritmogeometria. In questa tradizione la dimostrazione delle proprietà era lasciata alla evidenza visuale o a esempi generalizzabili, e non svolgeva alcun ruolo il principio di omogeneità, secondo il quale tutti i termini di una “somma” di grandezze devono avere la stessa dimensione (tutti i numeri sono segmenti, i prodotti di due numeri sono rettangoli e i prodotti di tre numeri sono parallelepipedi). Così, sia i babilonesi sia Erone potevano tranquillamente sommare aree e perimetri.

La geometria dell’abaco

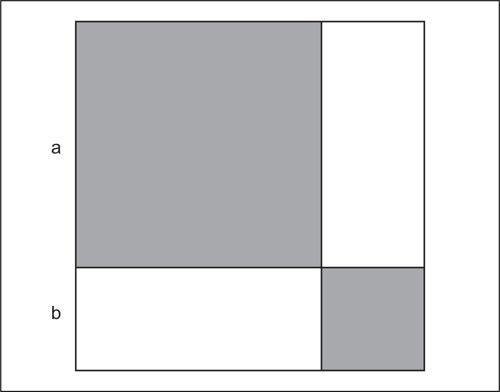
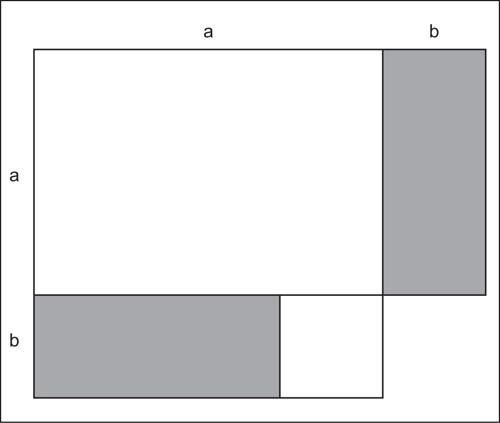
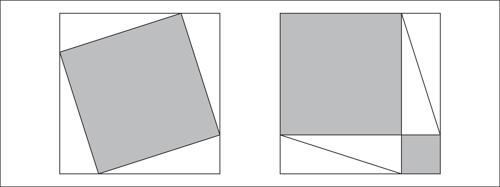
La geometria dell’abaco, che fu probabilmente la base dell’algebra geometrica, a noi pervenuta attraverso il ii libro degli Elementi di Euclide (secc. iv-iii a.C.), era probabilmente già in qualche misura nota ai babilonesi. Tramite essa si potevano mostrare proprietà che noi chiamiamo algebriche, come per esempio nelle figure 3 e 4 le formule: (a + b)² = a² + 2ab + b² e (a + b)(a − b) = a² − b² (si utilizza qui per comodità il linguaggio algebrico codificato nel xvii secolo: un anacronismo che verrà usato anche in seguito).

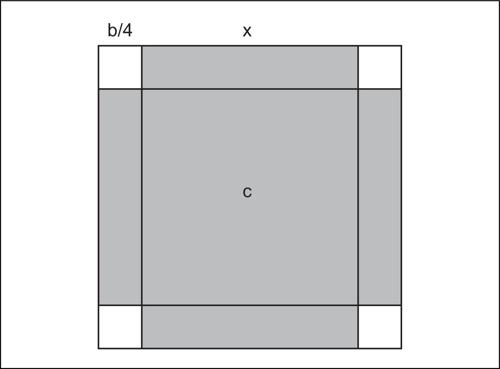
La figura 3 era anche la base della procedura pratica per calcolare la √(A) (il lato del quadrato A). Se infatti a è una buona prima approssimazione di √(A), allora √(A) = a + b, con b molto minore di a, e di conseguenza nel quadrato A il quadratino di lato b si può trascurare, ottenendo A ≅ a² + 2ab (corrispondente a una figura a forma di L, detta gnomone, differenza tra un quadrato e un quadratino in esso contenuto come in figura). Così la seconda approssimazione si ottiene aggiungendo ad a il valore approssimato b ≅ (A − a²)/2a. A tale approssimazione si può applicare di nuovo la stessa procedura per trovare una terza approssimazione, e così via.

Fino al Cinquecento l’algebra sarà intesa come tecnica pratica di risoluzione di problemi numerici, in cui le quantità erano intese geometricamente e trattate aritmeticamente, così che erano di fatto inconcepibili le equazioni di grado superiore a tre o i numeri negativi. Ciò era dovuto anche al fatto che non si era ancora sviluppato un linguaggio algebrico-simbolico che permettesse un calcolo agevole, linguaggio che verrà elaborato più tardi, nel Seicento, da Cartesio, Viète, Recorde e altri.

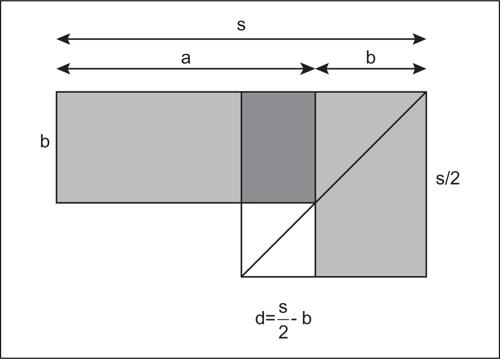
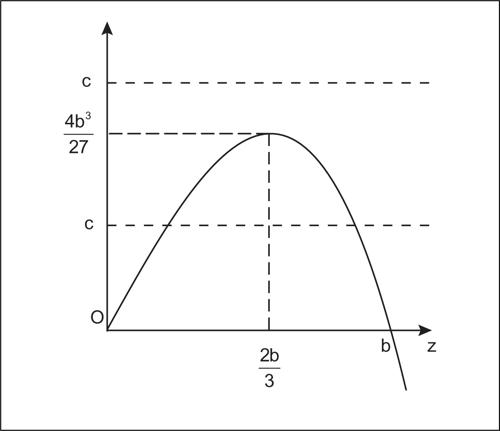
Un esempio complesso era la risoluzione della equazione di secondo grado in forma normale (nella forma, cioè, di una somma e un prodotto di due grandezze da determinare), della cui risoluzione si trova una plausibile traccia negli Elementi (teoremi ii.5 e ii.6, fig. 5).

In realtà, queste sono le uniche tracce di un approccio cognitivo geometrico, poiché sulle tavolette babilonesi si incontrano solo esempi di soluzione numerica. Ma poiché l’insegnamento nella tarda antichità era solo orale, ipotizzare un fondamento geometrico della procedura appare necessario per spiegarne, in assenza di formule, sia la descrizione che la memorizzazione. È infatti immediato ricavare la soluzione dell’equazione seguendo le indicazioni della fig. 5. Siano dati a + b = s, e ab = p. Ponendo d = |a − b|/2, a e b sono uguali a s/2 + d e s/2 − d. Lo gnomone di lati s/2 e d ha area p e quindi il quadratino bianco di lato s/2 − b ha area (s/2)² − p (che è nota). Da qui è facile calcolare b e poi a.

È da sottolineare come sia la concezione aritmogeometrica dell’abaco più che la stessa praticità a caratterizzare l’origine cognitiva e la collocazione sociale di questa tradizione. Compaiono infatti in essa anche problemi non pratici, puramente ricreativi, e in Diofanto hanno un ruolo centrale i problemi indeterminati (poco interessanti sul piano pratico), in cui le soluzioni possono assumere infiniti valori, vincolati per esempio dall’essere numeri quadrati.

La tradizione teorica

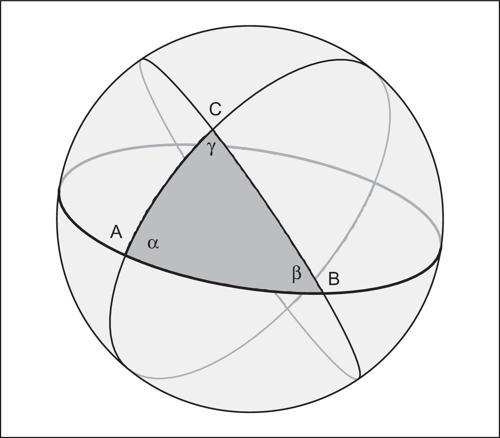
Di fronte alla tradizione pratica, nel v secolo a.C. se ne delinea una teorica, basata sulla geometria. Essa fiorisce per circa due-tre secoli, da Archita ed Eudosso sino ai grandi della matematica ellenistico-alessandrina − Euclide, Archimede, Apollonio − ai quali fanno seguito rari epigoni come Pappo. In tale tradizione la geometria non aveva alcun carattere metrico, essendo puramente teorica e centrata sulle proporzioni e sui concetti di uguaglianza e similitudine. Appariva netta in essa, contrariamente alla tradizione pratica, l’opposizione tra numeri e grandezze, tra aritmetica e geometria che durerà fino al rinascimento. E proprio tale opposizione spiega l’assoluta centralità della teoria dei rapporti e delle proporzioni nella matematica premoderna, come unico linguaggio per estendere alla geometria teorica concetti di natura aritmetica. Mentre l’aritmetica restava all’interno della tradizione pratica, la geometria teorica rompeva i ponti con la geometria dell’abaco: essa era assolutamente non metrica, giacché non esistevano in essa né lunghezze, né aree, né volumi, concetti che in qualche modo si rifacevano ad “approssimative” operazioni di misura. Oggi si dice (e qualcosa di simile dicevano i babilonesi) «l’area del cerchio è πr ²». Il matematico greco diceva invece «il rapporto fra due cerchi è il doppio rapporto dei diametri» (bisogna ricordare che i rapporti non erano numeri e doppio significava solo «composto con sé stesso», l’equivalente cioè di «elevato al quadrato», nella nostra terminologia).

Alle radici di questa geometria teorica vi erano le idee di uguaglianza e similitudine, che saranno il denominatore comune tra matematica e filosofia greca: nella prima, daranno origine alla teoria delle proporzioni e al sistema assiomatico euclideo, nella seconda alla dottrina delle idee/forme.

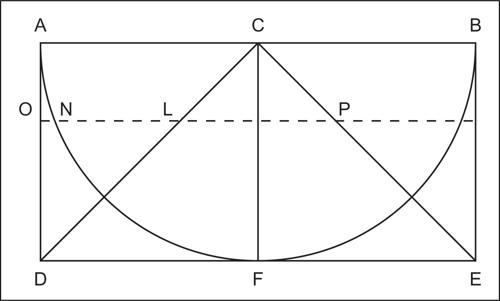
I rapporti erano relazioni tra quantità omogenee (impensabile quindi la velocità come rapporto tra spazio e tempo) e non erano numeri; anche le figure non avevano misure: non si sommavano le loro aree, bensì si univano le figure. Tra di esse si potevano fare confronti (una figura è “uguale” a un’altra se tramite opportune trasformazioni la si può trasformare in una figura sovrapponibile a essa, la prima è invece maggiore della seconda se, dopo le trasformazioni, la contiene). Le «trasformazioni equivalenti» erano le operazioni di dissezione e riassemblaggio e le equivalenze geometriche erano basate sugli assiomi dell’uguaglianza: nell’esempio in fig. 6 sono uguali i due rettangoli tratteggiati e i tre triangoli costruiti sulla stessa base. Esiste in Euclide un doppio criterio di uguaglianza: in primo luogo quello arcaico della sovrapponibilità, in secondo luogo la trasformabilità nel rispetto degli assiomi dell’uguaglianza.

I greci riuscirono a risolvere in generale il problema del confronto per le figure rettilinee, ma non per le figure curvilinee; era questo il problema della quadratura del cerchio: non si trattava di calcolare il π (per la cui approssimazione bisognerà attendere Archimede), ma di ricercare una sequenza di trasformazioni sulle figure che rendessero equivalenti un cerchio e un quadrato.

La tradizione teorica si tramandava attraverso la scrittura e la scuola, che nelle città greche andava assumendo caratteri moderni: relativamente di massa, spesso pubblica e fondata ai livelli elementari sul leggere, scrivere, far di conto: cioè manipolare segni.

Certo, ci furono nel mondo greco matematici in cui coesistevano entrambe le tradizioni: il “teorico” Archimede fu anche grande ingegnere e il “pratico” Erone (i sec. a.C. - i-ii sec. d.C.) fu anche ottimo geometra: non a caso a Erone si attribuisce la formula per il calcolo dell’area del triangolo a partire dalle lunghezze dei suoi lati, una regola che per il suo carattere metrico sarebbe stata impensabile per Euclide. Tuttavia la distinzione tra queste due tradizioni era molto più netta di quella attuale tra matematica pura e applicata, le quali condividono sostanzialmente metodi, concetti, linguaggi e istituzioni formative.

Aristotele e la strutturazione deduttiva

L’aspetto centrale della tradizione teorica era la ricerca di una strutturazione deduttiva della matematica, intuita già dai pitagorici. Tale sviluppo fu portato a compimento nel iv secolo dai matematici, soprattutto nell’ambiente dell’Accademia di Platone (427-347 a.C.), e fu teorizzato da Aristotele (384-322 a.C.), il più brillante degli allievi. Nei suoi libri Analitici prendevano forma la logica e la dottrina della scienza, a partire dalla dialettica platonica, dal lavoro dei matematici e dagli sviluppi della filosofia naturale. Alla base vi era un sistema di principi formali: il principio del terzo escluso («di un oggetto una qualsiasi determinazione deve essere o affermata oppure negata»), il principio di non contraddizione («non è possibile affermare e al tempo stesso negare qualcosa di un oggetto») e la verità per corrispondenza («è vero dire che è ciò che è e che non è ciò che non è, è falso dire che è ciò che non è e che non è ciò che è»).

Questo sistema di principi era valido solo al prezzo di frantumare il campo unitario platonico del sapere in un arcipelago di scienze “regionali”, all’interno di ciascuna delle quali i principi avevano piena validità. Il mondo aristotelico era fatto di sostanze individuali cui potevano essere associati attributi, soprattutto qualità e quantità. Ogni scienza si riferiva a un genere di sostanze ben determinato, sulla base di un sistema di assiomi (proposizioni note e universalmente accettate) e di definizioni di attributi appropriati per quel genere: la dimostrazione permetteva allora di costruire le verità di tale scienza. Le scienze non comunicavano tra loro, a meno che una scienza non fosse subordinata a un’altra (come la musica all’aritmetica o l’astronomia alla geometria).

Il ragionamento scientifico assunse la struttura del sillogismo, una forma di argomentazione in cui da due premesse con un termine in comune si ricavava una conclusione, che resterà per duemila anni la base della logica. Una forma semplice di sillogismo era: dalle due premesse «tutti gli ateniesi sono greci» e «tutti i greci sono mortali», si concludeva che «tutti gli ateniesi sono mortali». Premesse e conclusione potevano essere universali o particolari, affermative o negative; inoltre il termine comune poteva trovarsi in ruoli diversi nelle premesse. Aristotele studiò tutte le combinazioni possibili di sillogismo e individuò quelle che effettivamente erano valide. È facile infatti notare che certe coppie di premesse non permettono di ricavare alcuna conclusione: per esempio nulla si può dedurre sull’altezza degli ateniesi a partire dalle due premesse «qualche ateniese è biondo» e «qualche biondo è alto».

La logica rispecchiava perfettamente la fisica: la proposizione era descritta come soggetto + predicato, riflesso di un mondo fatto di sostanze con annessi attributi, e il sillogismo doveva in realtà riprodurre le relazioni causali, dove la parola causa aveva soltanto un senso esplicativo dei fenomeni (era la risposta alla questione «perché?»).

Tale dottrina della scienza restò pressoché invariata fino al rinascimento, anche se alla sua ombra sopravvivevano i sottili paradossi formali della logica, il più importante dei quali era il paradosso del mentitore: «io sto mentendo». Se questo enunciato è vero vuol dire che è falso, ma se è falso allora è vero. Un paradosso destinato a sopravvivere fino ai giorni nostri, legato alla compresenza nella stessa proposizione della negazione, dell’essere, della verità.

Matematica e filosofia

La matematica e la filosofia erano discipline “sorelle”. Entrambe concernevano la verità necessaria, l’essere e il discorso razionale, trovando le loro radici nel fatto che vedere, conoscere ed essere per i greci erano verbi profondamente connessi («idea» e «vedo» hanno un’origine comune e, per Aristotele, «non si può pensare senza immagini»); visuale era anche l’origine dei verbi di conoscenza come noéo, theoréo), la stessa «verità» (alétheia) era originariamente la negazione dell’oblio e del nascondere; gli enti matematici erano immanenti e immediatamente percepibili e nel contempo aspetti di conoscenza razionale.

Così, sul materiale ereditato dalla matematica pregreca, i pitagorici e successivamente Platone avevano eretto una filosofia complessa che da un lato accettava l’aspetto pratico della matematica (economico e sociale), e dall’altro concepiva il numero e la figura geometrica come parte integrante dell’ontologia in quanto mediatori di una realtà ideale ed elementi essenziali della stessa descrizione del cosmo: i pitagorici vedevano nel numero il costituente base della realtà, mentre per Platone gli enti matematici erano un ponte tra il «mondo delle idee» è la realtà naturale, così che Platone nel Timeo descriveva il cosmo con misure prive di ogni valore empirico ma tratte dai rapporti armonici musicali, ma al tempo stesso esortava Eudosso a «salvare i fenomeni» astronomici, trovandone una descrizione matematica. Su questa base tutta la tradizione pitagorica e platonica per millenni coltiverà una numerologia filosofica e teologica, ma anche una geometria descrittiva e l’idea di una presenza dei numeri nella realtà.

Diversa la collocazione della matematica nel sistema aristotelico delle scienze: da un lato essa riguardava l’essere reale nei suoi aspetti puramente logici in quanto scienza della struttura esplicativa del reale, scienza delle cause, della spiegazione dei fenomeni e quindi modello deduttivo per tutte le scienze, dall’altro il suo essere astrazione (rispetto alla materia e al divenire) ne faceva una sorta di impoverimento del reale: la matematica era un frammento del linguaggio naturale che forniva la spiegazione razionale dei fenomeni, ma la sua stessa certezza era un limite, segno di una “purezza” che finiva per configurarsi come “povertà” rispetto alla realtà naturale. Ne derivava un ruolo prevalentemente epistemologico e metodologico ben diverso dal ruolo ontologico che essa aveva in Platone.

La dimostrazione e l’incommensurabilità

Nella tradizione teorica non vi era spazio per l’algebra: tutto era percepito geometricamente, numeri inclusi. I soli enti utilizzati erano le figure geometriche e l’unica argomentazione era la dimostrazione. Le radici di questa tradizione si possono riconoscere nei pitagorici, i quali avevano verosimilmente rielaborato un’idea, importata dall’Oriente, di costruzione geometrica, cui veniva riconosciuto il ruolo di dimostrazione a partire da elementi, proposizioni e costruzioni più semplici. Infatti i babilonesi, pur non avendoci lasciato vere dimostrazioni geometriche o aritmetiche, conoscevano bene proprietà geometriche come il teorema di Pitagora: non solo qualche terna pitagorica, come (3, 4, 5) oppure (5, 12, 13), ma la proprietà generale, che probabilmente riconoscevano come costruzione geometrica evidente. La fig. 7 è una possibile costruzione geometrica per dimostrare il teorema. Non la si trova nei testi mesopotamici, ma appare nei più antichi testi cinesi e indiani.

Il ruolo della costruzione nella matematica greca è anche testimoniato dal rilievo che sin dall’inizio vi ebbero alcune costruzioni particolari, quali la quadratura del cerchio, la duplicazione del cubo, la trisezione dell’angolo.

Il passaggio dalla costruzione alla dimostrazione geometrica è uno degli episodi più affascinanti della storia della matematica. La dimostrazione all’inizio era probabilmente solo la descrizione per iscritto della costruzione di una figura, eseguita precedentemente per via orale e visuale: in greco diagramma significava «dimostrazione» oltre che «figura», e negli Elementi ogni dimostrazione era associata a una e una sola figura, talora di una banalità sconcertante. La semplice trascrizione sembra una novità irrilevante, ma i geometri greci si accorsero che così si evitava di scoprire erroneamente proprietà non generali ma valide solo per una particolare figura. Inoltre introdussero un nuovo tipo di dimostrazione, quella per assurdo, che non corrispondeva a nessuna costruzione effettiva, ma solo a una costruzione “impossibile”.

In effetti l’assurdo aveva già fatto la sua comparsa nella filosofia greca, per esempio nei paradossi di Zenone, ma solo come confutazione, come una sorta di espediente retorico per polemizzare con l’avversario. Nell’uso retorico delle contraddizioni erano maestri i sofisti, e la storia della logica antica è fondata sullo sforzo dei grandi filosofi vissuti tra la fine del v e il iv secolo, Socrate, Platone, Aristotele, di riportare le tecniche dell’argomentazione nel campo delle verità e della scienza. La semplice confutazione di un discorso avverso non è la dimostrazione della tesi contraria. Dimostrare che una tesi è assurda non significa dimostrare che la tesi opposta sia vera: a tal fine è necessario chiamare in causa il principio di non contraddizione e quello del terzo escluso, i principi formali della logica aristotelica.

Tra i risultati scoperti e dimostrati per assurdo appare uno dei teoremi più importanti di tutta la storia della matematica: l’incommensurabilità di lato e diagonale del quadrato, in termini moderni l’irrazionalita di √(2). Oggi se ne trova sui testi una dimostrazione per assurdo di tipo aritmetico: se diagonale e lato del quadrato fossero commensurabili, le loro lunghezze sarebbero nel rapporto m : n, con m e n interi e relativamente primi (se non lo fossero si potrebbero entrambi dividere per il fattore comune), in particolare non entrambi pari. Essendo 2 il rapporto dei quadrati costruiti su di essi (per il teorema di Pitagora), sarebbe m² : n² = 2. Da qui segue che m deve essere pari, poniamo m = 2k, e quindi sarebbe n² : k ² = 2. Quindi anche n sarebbe pari, contrariamente alla ipotesi secondo la quale m ed n sarebbero relativamente primi. Il che è assurdo. Ma in una tale dimostrazione il 2 appare come numero astratto, un sostantivo, mentre i numeri allora erano solo aggettivi. Tra il v e il iv secolo la dimostrazione doveva essere di tipo geometrico e prima ancora probabilmente fondata sulla teoria aritmetica della musica, la cosiddetta armonica. Infatti, la prima matematica greca originale, sviluppata dai pitagorici e non derivata semplicemente dall’Oriente, fu lo studio delle consonanze fra le note, misurate dai rapporti tra le lunghezze delle corde che davano tali consonanze: 1 : 2 (armonia di ottava), 2 : 3 (di quinta), 3 : 4 (di quarta).

Pitagora (570-490 ca a.C.) era originario di Samo. Coinvolto come tanti greci dell’epoca negli scontri politici della sua pólis, fu costretto a emigrare verso l’Italia meridionale, la Magna Grecia. Queste migrazioni erano un fenomeno diffuso nelle città elleniche dell’epoca. Provocate da ragioni politiche ed economiche, trapiantavano in un terreno vergine frammenti di società greca, creando un ambiente sociale più destrutturato di quanto fosse la pólis, che già risultava molto meno gerarchizzata rispetto alle società orientali e con una religione meno professionalizzata di quella delle caste di scribi del tempio orientale. I pitagorici furono una setta politico-religiosa che trasmutò le conoscenze tecnico-matematiche importate dall’Oriente in una «educazione liberale», in un sapere generale laico e religioso, politico e sociale, per governare le città della Magna Grecia: Metaponto, Crotone, Sibari, Taranto. Così aspetti tecnici come l’uso dei sassolini sull’abaco per studiare le figure geometriche sono forse all’origine di ipotesi filosofiche quale quella di studiare tutti i numeri, e anche tutti gli oggetti reali, in base alla loro forma geometrica discreta (in fig. 8: triangolari, quadrati, rettangolari, lineari ecc.).

Anche la musica aveva un’importanza a fini politici: essa non era un semplice intrattenimento, ma l’autentica colonna sonora della vita religiosa e sociale della pólis greca, al punto che Platone ripeterà: «Credo che i modi musicali non possano essere cambiati senza cambiare le leggi fondamentali della pólis».

Per governare occorreva dominare i modi musicali e questo creava problemi aritmetici: per esempio, per dividere in due parti uguali l’ottava occorreva trovare un x tale che 1 : x = x : 2. Oggi diremmo che x vale √(2), un numero irrazionale, ma per i pitagorici i numeri erano solo interi; solo verso la fine del v secolo a.C. Archita (430 ca-360 ca a.C.), l’ultimo grande pitagorico, scoprì che non esistevano soluzioni intere (o razionali). È questa probabilmente l’origine della incommensurabilità.

La matematica nella cultura antica

La geometria

Al centro della tradizione teorica si collocava la geometria, poiché la scienza greca era incentrata sulla presentazione visuale dell’essere, impermeabile al divenire naturale.

Come già si è accennato, era una geometria assiomatizzata e non metrica, perpetuata negli Elementi di Euclide, per duemila anni autentico monumento dell’umana ragione e culmine di una sequenza di libri di «elementi» apparsi nel iv secolo soprattutto intorno all’Accademia platonica, e derivati dall’idea pitagorica di una connessione costruttiva necessaria tra le proposizioni geometriche, da quelle più ovvie a quelle più complesse. Proclo scrive nei suoi Commentari al I libro degli Elementi che rispetto ad antichi libri di «elementi» Euclide aveva reso più rigorose e più astratte le dimostrazioni, sviluppandole per assurdo, e aveva esteso anche l’uso della teoria delle proporzioni.

Oltre alle definizioni, all’inizio del libro sono elencati postulati e nozioni comuni (assiomi). I primi hanno un carattere più costruttivo, le seconde appaiono come proprietà logiche dell’uguaglianza, probabilmente necessarie per trasformare antiche dimostrazioni basate sulla evidenza visuale in dimostrazioni rigorose per assurdo.

Le proposizioni appartengono poi a due categorie ben distinte, i teoremi e i problemi: i primi riguardano proprietà delle figure, i secondi invece costruzioni di enti geometrici, fondamentali in un’idea di dimostrazione emersa dall’idea di costruzione geometrica.

Il metodo euclideo è detto assiomatico-deduttivo, un’espressione usata anche per la matematica moderna, ma con un diverso significato. In realtà l’uniformità è solo apparente. Nella geometria greca, come del resto ancora oggi nell’insegnamento fino alle scuole superiori, non si fa differenza tra dimostrabilità e verità. Eppure la differenza è evidente. Si consideri per esempio la proposizione «in ogni triangolo la somma degli angoli interni è due angoli retti»; la sua dimostrazione è una paginetta di proposizioni concluse dalla frase «come volevasi dimostrare», e dopo la quale non sussiste alcun dubbio sulla validità del teorema. Se volessimo stabilirne la verità dovremmo invece prendere «tutti» i triangoli (ritagliati sul cartoncino, costruiti tramite le punte dei campanili, delle montagne e anche usando stelle e galassie) e calcolare su di essi la somma degli angoli interni. Sono due procedure del tutto diverse: la prima è unica anche se generale (su un triangolo «qualsiasi») la seconda è infinitaria (su «tutti» i triangoli); la prima è assolutamente certa, la seconda è sempre approssimata. Questa è la differenza tra sintassi (la manipolazione delle proposizioni secondo regole puramente formali e quindi indipendenti dal significato dei termini) e semantica (assegnazione del significato ai singoli termini e conseguente significato globale della proposizione). Per i greci questa distinzione non esisteva: ciò che era dimostrabile era vero e ciò che era vero era dimostrabile, eccezion fatta per gli assiomi e i postulati, la cui verità doveva essere del tutto evidente.

Diverse erano le conseguenze di questa coincidenza tra sintassi e semantica. In primo luogo, i termini tecnici della geometria euclidea non ricevevano il loro significato dalle definizioni, ma lo possedevano già come termini del linguaggio naturale, che la definizione si limitava a precisare. In secondo luogo, da Aristotele a Proclo, si distingueva tra teoremi in cui la deduzione aveva un ruolo «causale» e teoremi in cui la deduzione era puramente «formale», come per esempio nel teorema precedente, nella cui dimostrazione appaiono gli angoli esterni al triangolo, i quali non possono avere alcun ruolo causale sul triangolo (la somma degli angoli interni sarebbe due angoli retti anche se gli angoli esterni non esistessero).

In realtà la logica aristotelica aveva diverse radici: la teoria del sillogismo derivava dalla filosofia naturale (col sillogismo a mimare la relazione causale), la dottrina della scienza dalla geometria, e infine il sistema dei principi dalla dialettica. Così che, più che di una derivazione diretta del sistema assiomatico-deduttivo euclideo dalla logica aristotelica, si deve piuttosto parlare di una profonda affinità.

La conseguenza più celebre di questa coincidenza tra sintassi e semantica è stata per duemila anni la questione del v postulato, relativo alle parallele. Esso afferma: «Se una retta incidente due rette crea angoli interni sullo stesso lato minori di due retti, le rette, qualora prolungate all’infinito, si incontreranno dal lato sul quale gli angoli sono minori di due retti» (era una sorta di postulato di costruzione del triangolo); oggi si esprime nella forma: «Dati una retta e un punto a essa esterno, per tale punto passa una e una sola retta parallela alla prima». Tale postulato era ritenuto vero perché legato a tante altre proposizioni vere (costruzione del quadrato, teorema di Pitagora ecc.), ma non sembrava evidente. Di conseguenza doveva essere dimostrabile ma, nonostante decine di tentativi autorevoli, nessuno era riuscito a darne una dimostrazione. Solo nel xix secolo l’emergere della distinzione tra sintassi e semantica rese concepibili geometrie in cui tale postulato non era soddisfatto.

La dimostrazione procedeva da «cose più note» verso «cose meno note», dagli assiomi/postulati ai teoremi/problemi, una procedura nota anche come sintesi, che caratterizza lo stile di Euclide negli Elementi. Ma nella matematica greca appariva anche la procedura opposta, detta analisi, che partiva da «ciò che si cerca» per risalire a «ciò che già si sa». L’idea fondamentale era quella che invertendo le deduzioni di una delle due procedure si otteneva l’altra, ma in realtà A ⇒ B non implica B ⇒ A, così che per garantire la correttezza logica dei risultati l’analisi doveva sempre essere seguita dalla sintesi corrispondente.

Maestro dell’analisi fu Apollonio (262 ca-180 ca a.C.). Per capirne la grandezza basta pensare che sviluppò la teoria delle coniche (le figure ottenute per sezioni di un cono tramite un piano al variare della sua inclinazione: cerchio, ellisse, parabola, iperbole), nata probabilmente da esperienze di misurazione astronomica (meridiana, astrolabio), in quanto le stelle si muovono rispetto a un osservatore terrestre su cerchi che col vertice nell’osservatore formano un cono, la cui sezione con un piano è una conica. Apollonio ottenne per via geometrica tradizionale gran parte di quello che oggi si studia sull’argomento usando il formalismo algebrico.

Aritmetica teorica e aritmetica pratica

Del tutto diversa era la struttura dell’altra disciplina fondamentale, l’aritmetica. Gli Elementi includevano anche tre libri aritmetici (vii, viii, ix), in cui l’aritmetica veniva trattata rappresentando i numeri come segmenti. Era un’aritmetica basata su postulati e dimostrazioni, e sui concetti di rapporto e di proporzione, in un certo qual modo adottata dalla geometria.

L’aritmetica pratica aveva però una struttura molto diversa: non usava dimostrazioni ma esempi, ed era anche legata al calcolo e alla misura. Inoltre appariva organicamente connessa alla filosofia e alla teologia, dominata da un clima pitagorico e platonico fino alla fine dell’antichità: il testo più importante dell’aritmetica greca fu quello di Nicomaco, vissuto ad Alessandria tra i e ii secolo d.C., il più noto di una serie di testi in cui l’aritmetica veniva descritta all’interno della tradizione neoplatonica, senza alcuna parentela con la grande tradizione dei geometri teorici e nella quale ogni numero era figurato ed entrava direttamente nella costituzione stessa della realtà.

La notazione numerica dei greci era poco funzionale. Niente di strano che al mercato usassero una notazione simile a quella degli antichi romani, con un asta per indicare l’uno e poi l’aggiunta di un’asta per il successore, e l’uso delle iniziali dei numeri in greco per indicare numeri particolari, cinque (Π, pente in greco), dieci (Δ, deka in greco) ecc. Sorprende che i grandi matematici greci usassero per i numeri le lettere dell’alfabeto: α per l’uno, β per il due, e così via. L’alfabeto greco ha 24 lettere, aggiungendo tre lettere arcaiche di origine fenicia si arrivava a 27 simboli con cui denotare le nove cifre, le nove decine, le nove centinaia. E poi, dopo 999? Bisognava usare apici. Ma con un simile sistema erano molto difficili anche le somme elementari. Come si spiega l’uso di questa notazione davvero poco funzionale? In primo luogo, esso era probabilmente una conseguenza del fatto che il linguaggio della matematica greca era un frammento del linguaggio greco comune. In secondo luogo occorre osservare come questa rappresentazione introducesse il carattere ordinale e non solo cardinale del numero (e Piaget ha descritto come nel bambino il numero astratto nasca dal coordinamento tra i suoi aspetti cardinali e ordinali). In altri termini, la difficoltà nel calcolo era il prezzo da pagare per fare dell’aritmetica un frammento autonomo del linguaggio e concepire il numero come un ente astratto e non solo come un aggettivo.

Non esistevano né i numeri reali né i numeri razionali (eccettuate le parti, cioè le frazioni unitarie quale 1/n, molto usate già in Egitto). Ovviamente, al mercato esistevano dei modi pratici per trattare le frazioni, ma questo non aveva nessuna eco nell’aritmetica greca.

L’architettura complessiva della matematica era quella del quadrivio, in cui alle due discipline di base, aritmetica e geometria, si aggiungevano altre discipline che il medioevo chiamerà miste: in primo luogo astronomia e musica per completare il quadrivio, e poi anche ottica e statica. Altre scienze miste verranno aggiunte nel medioevo.

Queste discipline erano dette miste perché apparivano “inquinate” dalla fisica. La matematica, in quanto scienza dell’essere, non poteva essere applicata alla fisica né ad alcuni suoi settori quali la meccanica, la biologia, la psicologia, perché la fisica trattava del divenire (phýsis era la natura vista nel suo continuo fluire, e anche l’anima era considerata un ente naturale). In altri settori della fisica il divenire tuttavia non appariva: nella statica, ma anche in ottica, che non considerava la luce come “in moto”, ma ne considerava solo gli aspetti geometrici; in musica, in cui le consonanze erano trattate come rapporti fissi; in astronomia, in cui si ignorava il concetto di traiettoria dei corpi celesti e si studiavano solo le proprietà geometriche delle grandi sfere rotanti, ma fisse, nelle quali i corpi celesti erano incastonati. L’astronomia greca chiarisce il senso della geometria greca. Mentre i babilonesi avevano dato vita a un’astronomia d’osservazione, caratterizzata da grandi quantità di dati e una notevole capacità di previsione dei fenomeni astronomici (come le eclissi lunari), ma priva di un modello dei cieli, i greci elaborarono un’astronomia senza dati osservativi e costituita solo da un modello dei cieli, il cosmo, basato su sfere rotanti e complicato da sfere rotanti incastonate in altre sfere rotanti. Solo più tardi, soprattutto con Claudio Tolomeo, questo modello geometrico si arricchì dei dati osservativi e costituiì il cosiddetto sistema tolemaico che resse fino a Copernico. L’Almagesto (nome arabo che significa «il più grande») è il capolavoro di Tolomeo; insieme agli Elementi costituisce la grande eredità della scienza greca, e, insieme alle opere di Nicomaco, Erone e Diofanto, segna l’epoca d’oro della tradizione pratica in Alessandria.

Il continuo e l’infinito

L’idea di continuo non aveva natura immediatamente matematica, ma proveniva dall’indagine filosofica sull’essere e il divenire (il moto), iniziata dagli eleati (Zenone ne aveva rivelato i paradossi) e sviluppata da Platone e Aristotele, il quale ne aveva dato una doppia caratterizzazione tuttora valida: l’(infinita) divisibilità (dalla quale deriva l’idea moderna di denso in sé) e la dicotomia in parti con elemento comune (dalla quale deriva l’idea di continuità costruita sulla base delle sezioni di Dedekind). Era un concetto fondamentalmente fisico, estraneo alla matematica: il termine continuo (synechés), come opposto di discreto, negli Elementi non appare mai.

Anche l’idea di infinito non apparteneva alla matematica ed era un concetto sostanzialmente fisico. In Euclide il termine infinito (ápeiron) appare in forma solo avverbiale, per affermare che la retta può essere prolungata illimitatamente: era l’infinito potenziale («si può sempre aggiungere qualcosa») che si ritrova soprattutto nella serie dei numeri interi, mentre l’infinito attuale («non si può aggiungere nulla») era precluso, in quanto fonte di dubbi e paradossi. Questi due infiniti erano l’uno il contrario dell’altro, e non il contrario del finito. Anche le sezioni coniche, prima di Apollonio, erano costruite su coni finiti. Quella euclidea era una geometria piana senza il piano, una geometria solida senza lo spazio, una geometria di figure e solidi finiti che non richiedono un ambiente infinito che li contenga.

Lo stesso Apollonio nel suo studio delle coniche introduce rette di riferimento sulle quali “proiettare” le posizioni di punti delle curve, individuando segmenti tra i quali riconoscere relazioni geometriche nella forma di rapporti caratteristici delle curve (chiamati sýmptoma). Molti storici hanno creduto di riconoscere in queste enunciazioni i prodromi della geometria analitica moderna (con gli assi x, y, z di un sistema di riferimento, le coordinate dei punti, le equazioni delle curve). C’è però un’importante differenza: i concetti di Apollonio erano intrinseci alla curva (assi, diametri, tangenti), mentre quelli moderni sono estrinseci a essa e relativi invece a uno spazio indipendente che contiene la curva.

Tale preclusione nei confronti dell’infinito attuale si associava poi a quella nei confronti dell’esistenza reale del punto. Il punto infatti, come sarà poi per il numero reale, richiede una suddivisione infinita attuale del segmento, poiché una suddivisione infinita potenziale produce solo intervalli. E risulta chiara anche l’impossibilità di considerare un segmento come costituito dai suoi punti: come potrebbe un ente di grandezza finita essere costituito dall’unione di infiniti enti privi di grandezza? E si può concepire il punto immediatamente successivo a un altro punto? Non è possibile, poiché se tale punto è distinto allora tra i due punti esiste un intervallo il cui punto medio si colloca fra di essi, e quindi il punto trovato non è quello immediatamente successivo.

Aporie erano già emerse in Democrito (460 ca-370 ca a.C.), che si era posto il problema di considerare un cono come unione delle sue sezioni parallele alla base: se tali sezioni erano uguali allora la loro unione era un cilindro, se invece erano disuguali allora la loro unione era un cono “a gradini”.

Platone considerò i punti solo finzioni geometriche, in realtà non esistenti. Aristotele li ritenne esistenti ma solo in potenza, così che tutti i punti di un intervallo esistono in potenza ma non possono costituirlo poiché avrebbero bisogno a tal fine di esistere in atto, creando le difficoltà sopra accennate. E del resto, quando un punto divide in due un segmento, il punto stesso si duplica come estremo di entrambi, e il duplicato così nascerebbe dal nulla, ma nihil ex nihilo. L’idea di base era che l’essere del punto si esaurisse nella sua individuazione come estremo o intersezione, senza avere altra forma autonoma di esistenza.

L’infinito quantitativo

Ad Aristotele si deve l’inizio della teoria dell’infinito quantitativo, costruito sulla dicotomia della quantità in discreta e continua. Egli osserva come i numeri ammettano un minimo indivisibile (l’unità) ma non un massimo (l’infinito è solo potenziale), mentre le grandezze (geometriche), il cui paradigma era l’intervallo, non ammettano un minimo (sono potenzialmente divisibili all’infinito) ma abbiano un massimo (l’universo aristotelico era finito).

Le proprietà fisiche diverse da tempo e spazio (peso, velocità, calore ecc.) erano «qualitative». Quantità erano solo da un lato quelle geometriche e il tempo (continue), dall’altro i numeri e il linguaggio (discrete); per questo le velocità potevano essere confrontate solo come spazi percorsi in un tempo fisso o come tempi impiegati per percorrere una data distanza.

La misura era un concetto essenzialmente aritmetico: un numero “misurava” i suoi multipli, ne era cioè una parte. Al mercato si misurava il peso o la lunghezza, ma erano numeri accidentali. Mentre infatti l’unità di misura del gregge di pecore era intrinseca, sostanziale (la singola pecora), l’unità di misura della lunghezza era il braccio o il piede. Ma il braccio o il piede di chi? Era una misura puramente accidentale, e città diverse avevano unità di misura diverse. La geometria si doveva quindi strutturare senza una metrica. E anche queste misure accidentali erano sempre numeri interi, connesse tra di loro tramite fattori moltiplicativi accidentali e interi, come nelle misure inglesi: ci sono piedi e pollici, 12 pollici fanno un piede. Ma non è lo stesso che dire che 100 cm equivalgono a 1 m: infatti 12 è solo un rapporto accidentale tra unità autonome ed eterogenee, anche se convenzionalmente consolidato.

Per i greci, in realtà, irrazionali potevano essere i rapporti (relativi a grandezze incommensurabili), ma non i numeri. Per essi i numeri erano solo interi, cardinali e finiti, erano di fatto aggettivi (1, 2, 3, 4, 100, 1000, 10000 erano declinati in genere, numero e casi), erano molteplicità definite, attributi reali. Era anche difficile considerare l’insieme dei numeri, poiché questo significava ammettere l’infinito: così Euclide non dice «ci sono infiniti numeri primi», bensì «i numeri primi sono più di ogni molteplicità proposta di numeri primi», e nelle dimostrazioni non compare mai esplicitamente il principio di induzione completa, sempre sostituito da dimostrazioni (generalizzabili) per un numero finito, nonostante appaiano postulate proprietà sostanzialmente equivalenti, come «non è possibile una sequenza infinita decrescente di numeri interi».

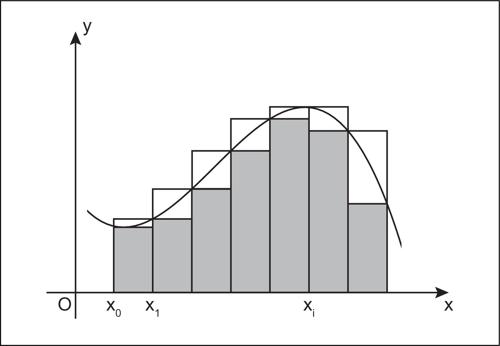
Persino Archimede, il più «infinitista» dei matematici greci, calcola la somma della generica progressione geometrica di ragione 1/4 e lunghezza n:

ma non riesce a intuire la somma della serie geometrica (per n → ∞).

Se si chiede oggi a uno studente di rappresentare con una immagine il sistema dei numeri, probabilmente egli disegnerà una retta, con un punto indicato con 0 e un altro indicato con 1. Traccerà cioè la retta numerica, con la quale si rappresenta oggi la corrispondenza biunivoca tra numeri reali e punti della retta, scrivendo un numero reale come due sequenze di cifre separate da una virgola, √(2) come 1,41421356…., π come 3,14159…, un numero reale generico come: … a₃a₂a₁a₀,a₋₁a₋₂a₋₃ … senza accorgersi del fatto che quella piccola virgola separa due universi radicalmente differenti in tutta la storia della matematica, che solo quattro secoli fa hanno trovato un punto di raccordo. La prima sequenza, a sinistra della virgola, appartiene al dominio dei numeri interi, alla numerazione, utilizzata per contare uomini e pecore, origine dei segni numerici. Al di là della virgola, la seconda sequenza appartiene a un mondo parallelo ma distinto: l’universo delle grandezze divisibili. Inoltre, mentre la prima sequenza è sempre finita anche se potenzialmente illimitata, la seconda può e deve essere attualmente infinita per denotare un generico numero reale.

Un greco avrebbe invece rappresentato il sistema dei numeri disegnando due semirette puntate verso il basso, come un lambda maiuscolo, Λ, tracciando quella che è appunto detta figura lambdoide. L’origine comune era indicata con 1, una delle due semirette segnata con i numeri interi 2, 3, 4, …, e l’altra con le frazioni 1/2, 1/3, 1/4, …, quelle che i greci chiamavano le parti.

L’uno non era un numero, ma il “seme” delle due sequenze, e lo zero non esisteva. Addirittura le definizioni euclidee erano date in modo da escludere anche l’angolo nullo o il rapporto nullo. La ragione di questa stranezza che durerà fino al rinascimento la si può leggere nel Sofista di Platone: «Poni che uno alla domanda “a che cosa può essere riferito questo predicato, il non essere”, osasse dare una risposta, ebbene, a quale oggetto e con quali determinazioni di quantità e qualità riferirebbe tale espressione? […] A ciò che noi indichiamo con l’espressione “ciò che è” non può riferirsi il non essere, neppure a ciò che indichiamo con l’espressione “qualche cosa” […] il singolare è segno di una cosa, […] il plurale di molte cose. E devi ammettere che chi non dice “qualche cosa” non dice niente in assoluto. Inoltre non possiamo ammettere che questo tale “usi una espressione”, ma non dica nulla; bisogna riconoscere che chi crede di dire ciò che non è, non usa espressione alcuna: non dice neppure […]». Il numero è sempre un numero di cose. Esistono quindi il singolare e il plurale, ma non esiste lo zero-ale. Esiste quindi l’uno, esiste il numero, ma non esiste lo zero. La matematica greca era un frammento della lingua greca.

Questo è un altro punto importante. La cultura occidentale, sin dal medioevo, è multilinguista: è consapevole dell’esistenza di molti linguaggi naturali (e delle relative traduzioni), e dell’esistenza di linguaggi formali artificiali (l’algebra, la logica, i linguaggi di programmazione ecc.). I greci erano rigorosamente monolinguisti, consideravano solo il greco. Certo, talora conoscevano altre lingue, ma erano solo “balbettii” (questo in origine il significato del termine «barbaro»). Anche le definizioni, come negli Elementi di Euclide, non servivano a introdurre nuovi termini nel linguaggio ma a delimitare e precisare in geometria l’uso tecnico di normali parole. Emblema di questa centralità teoretica del greco tra i greci è forse la parola lógos, che significava «parola», «discorso» ma anche «rapporto matematico», «ragione», «pensiero», «definizione».

I rapporti nel discreto e nel continuo

A Eudosso (408-355 a.C.) si devono alcuni dei risultati più importanti della storia della matematica. In primo luogo il modello geometrico dei cieli cui si è accennato nel paragrafo precedente. Un secondo contributo essenziale è la sua teoria delle proporzioni, una dottrina centrale per la matematica greca e medievale, essendo l’unico ponte tra discreto e continuo.

Il rapporto, il lógos, era inizialmete un concetto solo aritmetico, ma non un numero, bensì una relazione tra due numeri. Nell’antica aritmogeometria, ovviamente, questo concetto aritmetico poteva estendersi facilmente alla geometria: il rapporto tra base e altezza di un rettangolo nell’abaco era il rapporto tra il numero di unità su di esse. Ma la geometria teorica greca si era distaccata dalla matematica dell’abaco e l’incommensurabilità tra lato e diagonale del quadrato dimostrava che non si potevano ricondurre le figure geometriche a configurazioni di unità: per quanto si riducesse l’unità di misura non si riusciva a misurare contemporaneamente lato e diagonale del quadrato con un numero intero. Eudosso forse osservò come i rapporti tra segmenti incommensurabili, pur non essendo aritmeticamente definibili con esattezza, potevano essere aritmeticamente approssimati quanto si voleva. Già i babilonesi avevano trovato ottime approssimazioni numeriche per √(2). Le approssimazioni si potevano fare o per difetto o per eccesso. Per esempio un’approssimazione per difetto per √(2) è: 1 → 1,4 → 1,41 → 1,414 → 1,4142 →…, una per eccesso è: 2 → 1,5 → 1,42 → 1,415 → 1,4143 → … Qualunque numero razionale si prenda si può sempre dire se sia maggiore o minore di √(2).

Non potendosi esprimere con numeri un rapporto tra grandezze incommensurabili, la questione che Eudosso si pose fu se fosse possibile almeno dire se due rapporti a : b e c : d fossero uguali (l’uguaglianza e la similitudine erano i concetti base della geometria dell’epoca), ossia se valesse la proporzione a : b = c : d. In caso affermativo, le approssimazioni dei due rapporti dovevano essere comuni, e allora qualunque approssimazione m /n se era per eccesso per un rapporto lo era anche per l’altro, e quindi per ogni m e n si aveva che mb > na se e solo se md > nc. La notazione algebrica e aritmetica qui usata era inesistente a quei tempi, ma il ragionamento si poteva fare ugualmente nel linguaggio geometrico dell’epoca, e, considerando quella condizione non solo necessaria ma anche sufficiente, si otteneva la definizione eudossiana della uguaglianza tra rapporti: «Grandezze sono dette essere nello stesso rapporto, la prima con la seconda e la terza con la quarta, quando, per qualsiasi multiplo, gli equimultipli della prima e terza siano entrambi maggiori o uguali o minori dei corrispondenti equimultipli della seconda e della quarta». È nel libro v degli Elementi che viene delineata questa teoria delle proporzioni: i teoremi sono «teoremi generali», in quanto valgono per numeri e per grandezze geometriche, ma non configurarono mai una scienza generale e nel libro vengono riferiti alle grandezze semplicemente perché i greci non concepirono mai un genere comune a numeri e grandezze: la quantità era solo una categoria.

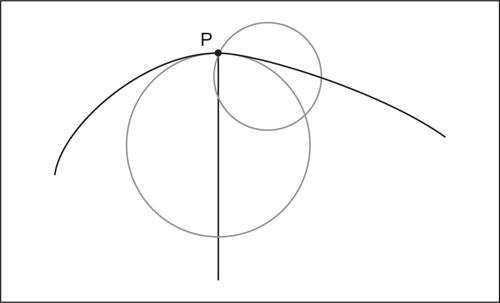
Due rettangoli le cui dimensioni avessero lo stesso rapporto erano simili, e avevano allora un rapporto che era il «doppio» (cioè il quadrato) del rapporto tra le dimensioni. Si dimostrava lo stesso risultato per i poligoni simili e si intuiva qualcosa di simile per i cerchi (fig. 9), considerando un cerchio come un poligono con moltissimi lati. Ma pensare a infiniti lati significava considerare un infinito attuale, qualcosa di inconcepibile.

Per affrontare questi problemi Eudosso ideò il metodo di esaustione.

Si supponga di voler dimostrare che il rapporto tra i cerchi è uguale al rapporto tra i quadrati con lati uguali ai rispettivi raggi (fig. 9). Lo si dimostra per assurdo: se si suppone che il rapporto tra i cerchi A : B sia minore del rapporto tra i quadrati C : D, allora il rapporto tra i quadrati sarà uguale al rapporto tra il cerchio A e una altra figura Σ > B. Si avrebbe allora A : Σ=C : D. Si circoscrivano al cerchio B poligoni regolari con un numero di lati crescente (e quindi con aree decrescenti): L₁, L₂, L₃, …, fino a trovare un poligono L_i, con tanti lati da rendere la sua differenza rispetto al cerchio B minore della differenza tra Σ e B. Questo poligono sarà così tale che Σ > L_i > B. Si costruisca un poligono con altrettanti lati M_i circoscritto al cerchio A. Tra i poligoni regolari vale il teorema che il rapporto tra due poligoni simili è uguale al rapporto tra i quadrati costruiti sui lati che hanno lo stesso rapporto dei lati dei poligoni, e quindi M_i : L_i = C : D. Ma A : Σ = C : D e quindi A : Σ = M_i : L_i e allora A : M_i = Σ : L_i. Ma il cerchio è minore del poligono a esso circoscritto e quindi Σ < L_i. Ma L_i era anche minore di Σ: il risultato è assurdo. Un analogo assurdo si verifica se si suppone che il rapporto tra i cerchi sia maggiore del rapporto tra i quadrati.

Nel ragionamento di Eudosso non appaiono né l’infinito né lo zero. Infatti il metodo di esaustione si basava sul teorema x.1 degli Elementi: «Fissate due grandezze disuguali, qualora dalla maggiore sia sottratta una grandezza maggiore della metà [in realtà questa condizione non è necessaria] e da quella restata fuori una maggiore della metà, e questo risulti in successione, sarà restata una certa grandezza che sarà minore della minore grandezza data». Poiché la minore delle due grandezze date può essere scelta a piacere il residuo può essere reso minore di ogni grandezza, ma senza mai ridursi a zero, poiché una grandezza non può diventare un non-essere e l’infinito non è un limite ma solo un luogo impraticabile.

In questo ragionamento le approssimazioni non sono più numeriche, come nell’argomentazione fatta per l’uguaglianza tra i rapporti, bensì geometriche, ottenute da poligoni circoscritti (o inscritti) con un numero crescente di lati, ma il ragionamento è analogo.

Il metodo di esaustione ha però un aspetto che lascia perplessi: può servire per verificare un’ipotesi sulla proporzione tra figure, ma non per scoprirla. In certi casi (come nel caso del cerchio) il rapporto tra le aree sembrava intuibile, ma in altri casi questo non accadeva, come nel caso del rapporto tra figure curve e rettilinee, dove occorre sempre tenere presente che in generale per i greci retto e curvo erano opposti e quindi inconfrontabili. Per esempio Archimede dimostra col metodo di esaustione che il rapporto tra un segmento di parabola e il triangolo isoscele in esso inscritto è 4 : 3. Ma questo rapporto era tutt’altro che evidente. Come l’aveva scoperto? Questi interrogativi presero ad affiorare tra i matematici del xvi secolo, quando si iniziò a studiare, capire e apprezzare gli scritti di Archimede. Molti sospettarono che Archimede disponesse di un “metodo” segreto per scoprire l’ipotesi “giusta”. Sorprendentemente, nel 1906, il filologo danese Johan Ludvig Heiberg (1854-1928) scoprì in un antico palinsesto un testo dove si parlava del «metodo di Archimede». La sorpresa doveva poi trasformarsi in ammirazione per il genio dell’autore: nella dimostrazione si faceva ricorso a una singolare fusione tra geometria e statica (teoria della leva), sviluppata da Archimede in diverse opere, costruendo una configurazione di equilibrio tra il segmento di parabola e il triangolo, tramite la realizzazione delle figure come unione delle loro sezioni parallele (segmenti, e quindi di dimensione inferiore alle figure).

Diofanto

Ad Alessandria è legato anche il nome di un matematico di cui non si sa quasi nulla e che resterà sconosciuto per tutto il medioevo, per diventare famoso con la nascita della matematica moderna: Diofanto (iii sec. d.C.), cui si deve l’ultima grande creazione della tradizione pratica dell’antichità: il primo simbolismo algebrico.

Sin dai babilonesi, l’algebra appare parte integrante della tradizione pratica, come soluzione aritmetica delle equazioni all’interno di una verosimile interpretazione aritmogeometrica dei problemi. In Diofanto si trova invece un autentico simbolismo: ς è l’incognita, probabilmente derivata da arithmós, Δ^γ è il suo quadrato, K^γ è il suo cubo, ɩ^σ sta per il segno di uguale (ísos), μ^O è la monade e ↑ sta per il segno meno. Come si è detto, i numeri venivano rappresentati alfabeticamente.

Eccone un’applicazione che si trova in un matematico bizantino del xiii secolo, editore di Diofanto, Massimo Planude (a sinistra nella tabella, a destra se ne dà una traduzione in forma moderna). Non si conoscono altre versioni precedenti e la notazione potrebbe quindi non essere del tutto quella originaria di Diofanto, ma una notazione simbolica analoga si trova in un papiro matematico che risale al ii secolo, e si può quindi ascrivere la nascita di questo simbolismo algebrico alla matematica pratica tardoantica.

Nell’esempio, si cercano due numeri la cui somma è 20 e la somma dei cui quadrati è 208.

Rispetto agli esempi concreti sulle tavole babilonesi, in Diofanto il problema viene posto in modo astratto. La risoluzione babilonese sembrava seguire i passi di una procedura ben definita, probabilmente legata alla costruzione di una figura (fig. 5) nella quale interpretare i dati numerici del problema e che permetteva di ricavarne la grandezza incognita, mentre Diofanto sembra maneggiare diverse condizioni in forma di equazioni che hanno la loro origine nell’algebra geometrica e nelle proprietà dell’uguaglianza, ma vengono ora manipolate per riscrivere le condizioni del problema. Il tempo della risoluzione non è più quello della costruzione, ma è puramente funzionale, nel senso che la soluzione si ottiene dalla sequenza di diversi passaggi a partire dai dati e dall’incognita del problema (spesso col vincolo di soluzioni intere), e la possibilità di iterare i simboli permette di esprimere potenze superiori alla terza, liberando così tali tecniche dalla limitazione del linguaggio geometrico. L’origine pratica e geometrica delle tecniche e dello stesso linguaggio algebrico appaiono però chiare anche in queste procedure simboliche, come nell’accettazione di sole soluzioni positive o nell’uso di un quadrato disegnato per denotare un quadrato aritmetico, oppure ancora nell’uso del termine «lato» (pleura) per il valore di cui si calcola il quadrato. Non esiste il prodotto tra incognite poiché il quadrato o il cubo non sono il prodotto dei rispettivi lati, ma figure; il prodotto tra un numero e l’incognita o la somma di termini sono date per semplice giustapposizione, come nell’algebra geometrica; i numeri sono semplici aggettivi che devono essere applicati a un’incognita o alla monade per diventare termini. Il segno ↑ compare come la parola «meno» nelle frasi in linguaggio naturale.

È da notare come il calcolo segua la stessa evoluzione della dimostrazione a partire da una comune origine (la costruzione della figura geometrica) tramite una traduzione sintattica, un’analogia questa tra calcolo e dimostrazione che si ripresenterà ancora in matematica. Quanto ciò sia peculiare si può cogliere osservando come le equazioni non comparvero mai nella matematica cinese, che proprio per questo, nonostante il grande sviluppo delle sue tecniche di soluzione dei problemi, non riuscì mai a creare una vera algebra.

La fine della matematica antica

La matematica antica finisce prima della caduta dell’impero romano. I romani avevano sviluppato una fugace passione per la cultura greca, all’inizio del periodo imperiale, al punto che in qualche misura l’impero era diventato bilingue: Cicerone per la filosofia e la retorica, Vitruvio per l’architettura erano state figure in cui riecheggiava la cultura greca. Ma progressivamente la romanità era tornata a prevalere. Del resto la stessa lingua latina mostra l’origine molto più pratica dell’idea romana di conoscenza: mentre i verbi greci di conoscenza richiamavano la visione e la memoria, quelli romani ricordavano l’esperienza pratica: sapio, sapientia («avere sapore»), puto, computo («potare»), penso («pesare»), verus («dritto, spiedo»), cultura («coltivazione»), scientia («tagliare»), forse anche cogito (da cogo, «raccogliere»). La divisione dell’impero in impero d’Occidente e Oriente fu non solo un espediente logistico, ma anche l’esito di una frattura culturale che, a partire dal iv secolo d.C., vide la scomparsa definitiva della matematica (e della filosofia) greca dall’Occidente; solo la retorica vi sopravvisse come traccia di quella antica influenza. La matematica si rifugiò allora nella sua terra d’origine, l’Oriente.

La fine dell’antichità e l’alto medioevo

Fra il v e il x secolo d.C. in Europa occidentale le popolazioni di cultura latina assistono al disgregarsi del loro mondo, sottoposte a invasioni e scorrerie continue dalla Scandinavia, dall’Asia, dall’Europa orientale e dai paesi islamici. La crisi, aggravandosi, travolge la produzione economica, il commercio interregionale, la cultura, e segna il tramonto delle città. Dopo il crollo dell’impero d’Occidente, le aggregazioni politiche che si costituiscono hanno in genere vita difficile: le popolazioni si rifugiano nei villaggi intorno ai castelli che diventano il cuore dei rapporti economici e sociali, delineando quella che viene detta la società feudale.

Il declino della cultura è profondo e inarrestabile: scompaiono le scuole, impallidisce la conoscenza del latino (dopo che quella del greco è caduta in un totale oblio) con l’unica eccezione degli ambienti religiosi, mentre nella vita quotidiana la lingua d’uso inizia a evolversi in quelle che diverranno le future lingue nazionali. Il latino rimane la lingua della cultura, unico strumento unificante della società europea, universale come la chiesa, ma senza vere radici sociali: il suo ruolo è del tutto diverso da quello dell’arabo nell’Islam (il Corano non si può tradurre, mentre i Vangeli sono multilinguistici sin dall’origine: la versione ufficiale della Bibbia è in greco e in latino già nella tarda antichità, e a partire dalla riforma protestante viene tradotta in tutte le lingue nazionali, senza che ciò ne infici il valore religioso), e anche quando nel rinascimento si cercherà una lingua originaria nella quale trovare il vero nome delle cose, la si cercherà nell’ebraico, o addirittura nel cinese, ma non nel latino.

Della matematica sopravvive solo la tradizione pratica nella sua forma più elementare, legata ai più semplici calcoli del commercio, dell’agrimensura e della architettura. Il Codex arcerianus, la principale fonte matematica dell’alto medioevo, raccoglie le conoscenze matematiche di carattere pratico diffuse negli ultimi secoli dell’impero d’Occidente e utilizzate dai gromatici, così chiamati per l’uso della groma, un lungo bastone provvisto in cima di un paio di sbarre orizzontali usato nei rilevamenti per traguardare.

La matematica e il cristianesimo

Unico riferimento culturale dell’Occidente europeo è il cristianesimo, ma il rapporto tra esso e la cultura classica antica è tutt’altro che lineare. Il cristianesimo antico da un lato si diffondeva soprattutto tra strati popolari urbani, dall’altro esibiva una struttura dogmatica sconcertante per la cultura classica (la divinità una e trina, il Cristo uomo e Dio, mangiare il corpo del Cristo, la resurrezione dei corpi ecc.). Era facile per i dotti pagani sottolinearne le assurdità: non è quindi strano che all’inizio si manifestasse l’opposizione tra la nuova religione e l’antica cultura. Tertulliano ne è il testimone più celebre: «Credo quia absurdum, […] tanto stolto da credere in un dio nato, e da una vergine […]. Morto è il figlio di Dio, è credibile poiché è irreale; e sepolto è risuscitato, è certo poiché impossibile». La contrapposizione è totale: «Che cosa hanno in comune Atene e Gerusalemme?».

Tuttavia, il cristianesimo sin dall’inizio è consapevole di doversi misurare con la cultura classica: Paolo predica all’Areòpago di Atene, Dionigi si converte. Così, lentamente, la parola di Cristo si diffonde fra i dotti e inizia una delle simbiosi culturali più importanti della storia.

La cultura delle nuove popolazioni barbariche si afferma nella cultura latina popolare: nelle saghe ed epopee con i cicli arturiano e carolingio, nella poesia col passaggio dalla quantità metrica all’accento e alla rima, nella musica con la nascita della polifonia e degli accordi di terza e sesta. La cultura romana, sconfitta sul terreno popolare, si poteva trincerare solo nella religione e nella filosofia, uniche sue forme di identità culturale nel medioevo. Le grandi questioni teologiche, come le lotte contro le eresie attraverso le quali si è andata formando l’ortodossia cattolica, diventano terreno di battaglia per quelle argomentazioni filosofiche di tipo dialettico e retorico che avevano caratterizzato la cultura classica.

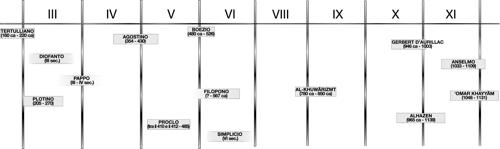
Agostino e l’estensione del concetto di quantità

Tertulliano era nordafricano e la sua formazione era prevalentemente giuridico-retorica. L’Africa settentrionale negli ultimi anni dell’impero romano è un centro culturale di primaria importanza. Da quelle terre e da quell’ambiente proviene anche il più importante pensatore cristiano della tarda antichità: Agostino (354-430). A lui si deve il primo grande tentativo di fondere il platonismo con il pensiero cristiano, ma è anche uno dei pochi e incerti canali della trasmissione del pensiero matematico antico alla cultura medievale: a lui si devono nel De quantitate animae poche pagine contenenti semplici definizioni (punto e segno, figure geometriche) che si ritrovano negli autori medievali. Agostino pone anche un problema nuovo: si può parlare di quantità dell’anima? O di quantità della carità? L’anima non è un corpo, ma è in un corpo e le sue immagini e i suoi ricordi hanno dimensioni; si può parlare di una «grande» anima o di una «maggiore» carità. E le anime si possono anche contare. Si profila così la possibilità inedita di estendere la quantità al di là delle grandezze geometriche, del tempo e del numero di cose.

La cultura nel medioevo

A questo punto si impone un’osservazione generale sull’epoca che si apre: il medioevo, usualmente ritenuto una lunga sequenza di secoli bui, in cui nessuna luce rischiarava il pensiero, e dai suoi stessi difensori esaltato per il trionfo della fede religiosa e dell’irrazionalità cui il rinascimento e la rivoluzione scientifica avrebbero posto fine. Questa lettura ha portato a ignorare il fatto che aspetti essenziali della nuova scienza, del tutto eterogenei rispetto alla scienza antica, siano apparsi già nel medioevo. Lo stesso intellettuale europeo nasce non nell’antichità ad Atene o Alessandria d’Egitto, ma in quelle lande desolate che nell’alto medioevo costituivano l’Europa. Sua prima incarnazione è il monaco benedettino, nel cui precetto «ora et labora» scompare quella scissione netta tra scienza e tecnica tipica della cultura antica, che si formava nella schola, parola che in greco e latino significava «ozio». Nel monastero si studia, si ricopiano i codici antichi, si prega e parimenti ci si dedica all’orto, alla falegnameria, al laboratorio, lavorando pietra e metalli. Le minime competenze matematiche che servivano ai muratori per edificare le chiese antiche si affiancavano a quelle necessarie per calcolare la data della Pasqua. Nella conservazione del patrimonio culturale dell’antichità i monasteri ricoprivano un ruolo non privo di contraddizioni: da un lato molti monaci avevano l’abitudine di cancellare antiche pergamene contenenti testi classici del pensiero greco per scriverci le loro omelie, d’altro lato nell’alto medioevo i monasteri divennero gli unici luoghi in cui quegli stessi classici venivano ricopiati e letti.

Il mondo così come era concepito dal cristianesimo non era eterno e immutabile o ciclico come per gli antichi greci, ma creato da un dio artigiano (artifex) talora rappresentato con il compasso e gli attrezzi intento a “produrre” l’universo, un dio descritto poi nel rinascimento come il divino «orologiaio» creatore della «macchina» del mondo. Il creato era uniforme, fabbricato da Dio: non c’erano divinità, né negli astri né nei fiumi, e appariva ingiustificata la distinzione tra una fisica terrestre e una celeste, così come inaccettabile ogni carattere divino della natura.

Un nome centrale nella storia della trasmissione del sapere logico e matematico antico al medioevo latino è quello di Boezio (480 ca-524 o 526), intellettuale emblema del tentativo dei popoli latini di salvare la propria identità culturale nella nascita dell’Europa all’interno dei nuovi stati barbarici. Senatore al tempo di Teodorico, ne divenne il consigliere, ma non poté evitare di essere coinvolto nelle trame di corte, in un’epoca in cui l’impero bizantino, romano e cristiano, era ancora presente in Italia. Venne giustiziato e la sua morte interruppe il suo tentativo di tradurre in latino tutti i classici della matematica e della logica antica. Alcune sue opere sono andate perdute e quelle rimaste costituiscono il nucleo principale delle conoscenze scientifiche dei greci note nell’alto medioevo europeo: un libro di aritmetica e uno di armonia ricavati da Nicomaco, un libro di geometria che riporta i primi tre libri degli Elementi, quasi del tutto senza dimostrazioni. In realtà di quest’ultimo ci sono pervenute due versioni, entrambe però ascrivibili ad autori medievali successivi, anche se probabilmente basate pure sul testo di Boezio. Sebbene concettualmente molto inferiori all’opera di Euclide, questi testi includono alcune aggiunte abbastanza caratteristiche del pensiero medievale. Così la Geometria ii inizia definendo la misura, che negli Elementi era concetto puramente aritmetico, come «qualunque cosa si definisca» non solo in termini di lunghezza, ma anche di peso, capacità e «animo». Dichiara il punto (che in Euclide era caratterizzato solo dall’essere «senza parti») principium mensurae, include un libro di proposizioni metriche e considera la geometria utile ai meccanici, ai medici e ai filosofi: si tratta quindi di una rilettura (caratteristica dell’alto medioevo) della geometria teorica all’interno della tradizione pratica, con l’idea agostiniana dell’estensione della categoria della quantità al di là delle grandezze geometriche e dei numeri.

Le conquiste del medioevo

L’estensione del «regno della quantità» è una delle novità medievali che risultano cruciali per la nascita della scienza moderna. Il superamento della distinzione tra scienze e tecniche e la progressiva fusione fra tradizione pratica e teorica ne sono un altro aspetto essenziale, anche se nelle università medievali e nell’umanesimo riapparirà una forma di elitarismo della teoria rispetto alle tecniche: di fatto le università del basso medioevo interrompono un processo di osmosi tra scienza e tecnica che invece era evidente nell’alto medioevo, e riemergerà nel rinascimento.

Un altro aspetto essenziale che compare nel medioevo è il superamento dell’idea greca di scienza come pura scienza di universali, per cui era scienza descrivere col sillogismo la causa delle eclissi, ma non era scienza individuarne la data, fatto tecnico che solo con Claudio Tolomeo tornò a caratterizzare l’astronomia. Le idee generali della filosofia naturale aristotelica nel medioevo si estendono invece ai fatti individuali e tecnici, segnando il trionfo di scienze quali l’astrologia e l’alchimia.

L’attenzione verso l’individuo, una delle tematiche più innovative del pensiero cristiano, trova nel francescanesimo la sua lettura più radicale; questo aspetto sarà destinato a caratterizzare una scienza che parla anche di singole cose e non di sole idee, nella quale i fatti individuali non sono solo istanze individuali di attributi universali delle specie, ma fatti complessi, effetti di innumerevoli relazioni causali. Così si assiste al formarsi di un sistema culturale medievale intorno al pensiero cristiano in cui cominciano a delinearsi i caratteri fondamentali della scienza moderna.

Questi processi culturali nell’Occidente si affiancavano a una crescente capacità di assimilare e trasformare novità tecnologiche in gran parte importate dall’Oriente, che riguardavano le tecniche agricole, i finimenti del cavallo, l’uso dei mulini per produrre energia, nuove tecniche costruttive: acquisizioni destinate a trasformare non solo l’economia ma anche il potenziale bellico degli europei. Tuttavia, anche se si intravedevano tutte queste novità, l’Europa occidentale nell’alto medioevo restava, rispetto ai grandi imperi orientali, un continente sottosviluppato.

L’impero romano d’Oriente durò mille anni dopo la caduta di quello d’Occidente. E nei secoli tra la fine dell’antichità e l’inizio del medioevo, soprattutto ad Alessandria, esso fu la dimora della cultura classica. Qui operavano gli ultimi grandi filosofi, da Plotino, padre del neoplatonismo, a Simplicio, uno dei massimi commentatori di Aristotele. Interessante la figura di Giovanni Filopono (490 ca-570), altro esponente della fusione tra pensiero classico e cristiano, e primo pensatore a sottoporre la filosofia naturale dominante, quella aristotelica, a una critica moderna. Aristotele infatti rifiutava il vuoto e l’idea di uno spazio tridimensionale “contenitore” delle cose, considerava la fisica dei cieli e quella terrestre del tutto diverse, riteneva il mondo eterno, considerava la materia una realtà solo negativa, priva di proprietà e dimensioni, e credeva che la velocità di caduta di un grave crescesse col peso. Tutte tesi che Filopono rigetta, anche se occorrerà aspettare un millennio per vedere quelle critiche pienamente accolte.

La matematica nell’Islam

Nell’alto medioevo in Oriente, a differenza di quanto avviene in Occidente, la tradizione matematica pratica vive un periodo di intenso sviluppo: la tradizione della matematica babilonese in Mesopotamia si sovrappone ad aree di cultura greca, dall’Egitto alla Siria, ad aree più orientali, dalla Persia all’Afghanistan, in cui si avverte l’influenza della matematica indiana. Saranno soprattutto queste aree più orientali, intorno alla Baghdad delle «mille e una notte», il centro della matematica islamica.

In queste aree nel vii secolo si afferma l’Islam; caratterizzato da un’incredibile capacità di espansione, l’Islam si diffonde dalla Spagna all’India occidentale, lungo quella che era sempre stata la grande via di comunicazione tra Occidente e Oriente. La matematica islamica affonda le sue radici nella tradizione pratica ma si mostra capace di comprendere anche gli aspetti più avanzati della tradizione teorica greca, e soprattutto di sviluppare in modo originale aspetti della matematica che saranno alla base della scienza moderna.

Oltre agli importanti sviluppi nell’ottica, nell’alchimia, nella trigonometria, nell’astronomia, vanno soprattutto sottolineati i contributi della matematica islamica in due campi: la notazione numerica decimale di origine indiana e l’algebra.

Il sistema decimale e l’idea di algoritmo

La nuova notazione numerica, col passaggio al sistema decimale indoarabo, si diffonde a partire dal testo di al-Khuwārizmī (780 ca-850 ca). Questo sistema era apparso in India almeno dal 595. In genere questo passaggio viene considerato come puramente notazionale e la sua importanza viene ascritta soprattutto al carattere posizionale del sistema, in cui il valore di ogni simbolo è legato alla sua posizione all’interno del numero (un 3 può valere tre unità, tre decine, tre centinaia ecc. a seconda della sua posizione). Questo aspetto tuttavia può essere ritenuto secondario; già il sistema sessagesimale babilonese era posizionale e, ancora più importante, anche nello stesso abaco i sassolini avevano un valore posizionale. La novità essenziale è invece la nascita dell’idea di algoritmo, come procedura di manipolazione sintattica dei segni numerici. Infatti nella matematica dell’abaco i segni numerici non entravano nel calcolo, ma servivano solo per registrare i dati iniziali e finali. Le cifre indoarabe sono invece gli ingredienti essenziali degli algoritmi con cui le operazioni sono svolte.

Il passaggio dall’abaco agli algoritmi sembra essere stato nei paesi islamici meno travagliato di quanto non sia stato in Europa. Probabilmente tra i due metodi vi erano punti di contatto: forse all’inizio gli stessi calcoli coi numerali venivano fatti sull’abaco (i numerali indoarabi occidentali venivano detti ghubar, «polvere»). Nell’Islam non ci sono tracce di una contrapposizione rigida fra i due metodi: del resto, come già detto, lo stesso abaco aveva una struttura di base posizionale e in genere anche decimale per gli interi: forse il nuovo sistema era inizialmente soprattutto un uso di simboli nel calcolo con l’abaco.

Va rilevato che l’idea di algoritmo porta con sé un’inaudita estensione del concetto di numero, in quanto gli algoritmi vengono estesi rapidamente alle frazioni. Tra i segni appare anche lo zero (un circoletto per denotare la colonna vuota sull’abaco), mentre l’uno viene trattato come le altre cifre (come nell’abaco). L’antica idea di numero si sfalda così a partire dal suo uso algoritmico, mentre nel contempo si attenua la distinzione fra la tradizione pratica e quella teorica. In astronomia e trigonometria i rapporti incommensurabili appaiono come misure di intervalli, diventando di fatto numeri, ignorando la complessa teoria dei rapporti di Eudosso: Omar al-Khayyām ritiene che l’essenza del rapporto debba essere la sua misura, e si chiede se «il rapporto sia legato al numero non per natura, ma con l’aiuto di qualcosa di esterno, o il rapporto sia per natura un numero e non abbia bisogno di niente di esterno»: il rapporto è ormai un numero. Dopo sei secoli Newton definirà viceversa il numero (reale) come un rapporto tra una grandezza e un’altra grandezza della stessa specie, intesa come unità.

I numeri diventano segni: non sono più caratterizzati come attributi delle cose, ma definiti operativamente dagli algoritmi e dalle misure. L’estensione dell’idea di numero arriva così quasi a prefigurare l’idea di numero reale e l’isomorfismo tra il continuo geometrico della retta e il continuo numerico dei numeri reali.

Ma l’idea di numero (intero positivo) come molteplicità tarderà a scomparire, così che l’estensione della notazione indoaraba ai decimali dovrà attendere Stevin, e nel frattempo le grandezze trigonometriche continueranno a essere indicate, in Oriente come in Occidente, come numeri interi relativi a cerchi di raggio grande, tanto più grande quanto migliore deve essere la loro approssimazione (Regiomontano userà un raggio di 600 milioni!).

L’algebra

La seconda grande novità introdotta dalla matematica islamica è lo sviluppo dell’algebra sintattica.

Anch’essa appare nell’opera di al-Khuwārizmī, che non sembra però essere stato influenzato da Diofanto. Rispetto all’algebra babilonese, l’algebra islamica ha di fatto una struttura anfibia: da un lato vi è la tecnica sintattica per trasformare il problema in equazione, dall’altro permane la tecnica geometrica per risolvere le equazioni.

La prima tecnica è fondata sull’intuizione che un problema è già una equazione tra due espressioni e sull’esperienza che tale equazione può essere trasformata con semplici manipolazioni; per esempio, un termine può essere spostato da un membro all’altro dell’equazione semplicemente cambiandogli il segno. Oggi si eseguono queste trasformazioni su equazioni scritte in linguaggio simbolico; gli arabi lo facevano operando sulle frasi scritte in linguaggio naturale, ma anche così la manipolazione algebrica trattava le parole sintatticamente, cioè come segni. Con queste trasformazioni le equazioni potevano essere poste in una forma canonica: tutte le equazioni di secondo grado potevano essere ridotte a una delle sei forme seguenti (tradotte in linguaggio algebrico moderno) con l’eventuale coefficiente di x ² posto uguale a 1 dividendo ambo i membri per esso:

Mentre nell’approccio babilonese ogni problema sembrava fare storia a sé, ora tutti i problemi erano riducibili a una delle sei forme canoniche, e quindi andavano studiate solo sei procedure di risoluzione. A noi esse appaiono equivalenti (spostando i membri e cambiandoli di segno), ma non ai matematici dell’epoca, in quanto il “senso” di queste equazioni restava geometrico e in tale approccio tutte le grandezze dovevano essere positive, così che le sei forme richiedevano soluzioni distinte.

Rispetto a un’equazione completa di secondo grado (x ² + bx + c = 0), nelle prime tre manca un termine e risultano facili da risolvere. La tecnica di risoluzione delle altre aveva sempre una natura geometrica. In fig. 10 è riportata la soluzione dell’equazione della forma (in traduzione latina) census et radices equantur numero, cioè x ² + bx = c.

Il quadrato al centro ha lato x, i quattro rettangoli laterali hanno lati x e b/4, e quindi la figura a croce punteggiata ha area c. Con i quattro quadrati angolari di lato b/4 il quadrato totale ha area c + b²/4 (che è nota) e lato x + b/2. La radice dell’area meno b/2 dà allora x. Da notare la somiglianza tra questo completamento del quadrato geometrico con il completamento del quadrato del binomio algebrico che si utilizza oggi per ricavare la formula risolutiva della precedente equazione di secondo grado.

Le tecniche di manipolazione simbolica si estendevano poi al calcolo di espressioni contenenti radicali o radicali doppi come per esempio (usando una notazione moderna)

molto utili quando (a² − b) è un quadrato perfetto. I matematici arabi raggiunsero una grande capacità di trattare geometricamente relazioni numeriche. Un esempio brillante si trova nell’opera del medico e scienziato arabo Alhazen (965 ca-1039), considerato tra l’altro il fondatore dell’ottica moderna, nel calcolo di una relazione generale tra le somme delle potenze K-esime dei primi N interi, in termini moderni:

Dalla fig. 11

si ricava direttamente

Infatti il membro di sinistra è semplicemente l’area del rettangolo totale, nel membro di destra il primo termine è la somma dei rettangoli “verticali” e la sommatoria successiva è la somma dei rettangoli “orizzontali”. Da questa formula si possono calcolare iterativamente tutti gli S_N,K.

L’importanza dei segni

Non deve sfuggire la sottile omogeneità sintattica che lega la nuova notazione numerica indoaraba alla nuova algebra simbolica: come già in Diofanto, il trattamento sintattico algebrico affonda le sue radici nella manipolazione aritmetica della tradizione pratica, in cui è assente l’opposizione tra numeri e grandezze. Questo è in fondo anche abbastanza ovvio poiché entrambe le tecniche nascevano su una base aritmogeometrica; ora accade che questi aspetti della tradizione pratica causino mutamenti epocali nella stessa struttura cognitiva della matematica. Sostanzialmente si delinea un ruolo inedito dei segni, che nella matematica greca avevano un ruolo secondario. Tanto l’estensione del concetto di numero e la numerazione indoaraba quanto la nascita della manipolazione algebrica simbolica significano che l’idea di quantità non è più caratterizzata dalla confrontabilità e dall’enumerazione, ma dal trattamento sintattico. I numeri e le grandezze cominciano a uniformarsi nell’essere soprattutto segni, e i segni cominciano a essere i componenti essenziali dell’algoritmo, che a sua volta si caratterizza come manipolazione di segni secondo regole.

La matematica in Europa

Nel secolo xi l’Europa occidentale comincia a risollevarsi dalle condizioni miserabili dell’alto medioevo. Riprendono i commerci, rifioriscono le città e gli eserciti europei cominciano ad affermarsi nelle guerre contro l’Islam: la reconquista della Spagna e le crociate ne saranno gli aspetti più evidenti. In questa fase l’Europa si apre alla matematica islamica. Soprattutto in Spagna vengono importate tecniche e strumenti, e sono tradotti in latino testi sia islamici sia di origine greca. L’imponente lavoro di traduzione è reso possibile dal carattere multilinguistico della civiltà medievale che in Spagna raggiunge il suo culmine in una città come Toledo, dove convivono dotti che parlano più lingue (l’arabo, il latino, l’ebraico). Si traducono testi medici, astrologici e alchimistici e anche i classici della matematica e il corpus aristotelico.

Emblematica di quest’epoca è la figura del francese Gerbert d’Aurillac (946 ca-1003), che fu papa col nome di Silvestro ii. I suoi viaggi lo avevano condotto in Spagna, dove aveva avuto contatti con la scienza araba e da dove si era procurato strumenti astronomici; in seguito a tale esperienza si era costruito un abaco che differiva da quelli tradizionali per il fatto di usare, al posto dei sassolini, gettoni con incise le cifre indoarabe, così che invece di mettere sulle colonne dell’abaco quattro sassolini si metteva un gettone col numero 4 (non serviva alcun gettone per il numero zero, che nell’abaco coincideva con la colonna vuota). Forse quest’abaco particolare è una traccia della derivazione della nuova aritmetica da quella antica legata all’abaco. Anche in Europa è la tradizione pratica a dominare, e si diffondono procedure approssimate per la costruzione di figure geometriche non realizzabili elementarmente con riga e compasso, come l’ettagono. Come nell’Islam, si attenua la distinzione tra tecniche (meccanica, ottica, scienza dei pesi, statica, architettura, medicina) e scienze.

La diffusione delle nuove tecniche matematiche in Europa sarà tuttavia più lenta e incerta che nei paesi islamici e le procedure di calcolo resteranno a lungo quelle tradizionali. Per esempio a Gerbert d’Aurillac veniva posta la questione se il triangolo equilatero, il cui lato ha lunghezza 7 piedi, possedesse area 28 (7 ⋅ 8/2) o area 21 (7 ⋅ 6/2). Rispondeva 21, valore approssimato corretto, derivato dalla regola secondo cui l’altezza del triangolo equilatero è circa 1/7 più piccola del suo lato (fig. 12).

Interessante osservare che il 28 derivava invece dalla regola dei numeri triangolari. Infatti aritmogeometricamente sono 28 le monadi che costituiscono il triangolo (fig. 13).

Altro esempio è un calcolo che appare in un testo del xii secolo: «Il nostro algorista ha realizzato la divisione di 100 librae per 11 merciai. La singola libra restante dalla divisione egli la pone uguale a 40 solidi. L’ulteriore resto di 7 solidi viene trasmutato in nummi, dei quali 12 fanno un solidus. Di nuovo rimangono dalla divisione altri 7 nummi, e per questi si devono comprare uova delle quali i merciai si devono servire a pranzo. Per ogni nummus si ottengono 13 uova, in totale così 91 e si dividono di nuovo queste per 11, così rimane ancora un resto di 3 uova. Queste si devono dare in ricompensa a chi ha realizzato la spartizione o barattare con del sale che debba essere mangiato probabilmente sulle uova». I numeri sono ancora solo interi con diverse unità di misura, eterogenee ma connesse tra di loro mediante rapporti di conversione fissi.

La distanza tra scienza e tecnica

Alla fine dell’alto medioevo l’Europa sembrava destinata a seguire anch’essa la strada della progressiva attenuazione della separazione tra scienza e tecnica, notata già nei monasteri all’inizio del medioevo. C’era un diffuso pragmatismo nello studio anche dei problemi matematici; per esempio, sembrava strano ritenere rette e curve inconfrontabili: bastava un filo piegato in modo da coincidere con la curva e poi raddrizzato per poterlo misurare.

Ma verso la fine dell’xi secolo si profila una trasformazione profonda nella realtà culturale europea: la nascita delle università. Con esse il solco tra scienza e tecniche si approfondirà di nuovo, fino alla fine del medioevo. Nelle università si leggono gli Elementi di Euclide ma, mentre nella matematica islamica il testo aveva il ruolo di fonte di conoscenze utilizzabili, nell’università medievale esso apparirà sempre come riferimento «ideologico» di un sapere scientifico assolutamente certo e necessario, ma indifferente alle tecniche: nell’Islam si apprezzano i risultati euclidei, in Europa si apprezza lo stile euclideo. Non sarà però un passo indietro, ma solo una deviazione per aprire la via a una nuova scienza dai caratteri assolutamente inimmaginabili.

Il basso medioevo e il rinascimento

Intorno all’anno 1100 un giovane francese figlio di nobili di provincia, Pietro Abelardo (1079-1142), si recava a Parigi per completare la sua formazione. Da alcuni decenni l’insegnamento stava rifiorendo in Europa e stava spostandosi dai monasteri benedettini e cisterciensi nelle campagne verso le scuole delle cattedrali nelle città; i maestri delle università erano spesso legati al mondo religioso e nel xiii secolo provenivano di frequente dagli ordini mendicanti, domenicani e francescani.

Il rifiorire delle città è forse il dato più rimarchevole dell’Europa dell’epoca, dovuto non solo al risveglio dell’economia e dei commerci, ma anche al fatto che le città erano un luogo più aperto e dinamico, meno soggetto ai condizionamenti della società feudale in disfacimento: «l’aria della città rende liberi», recitava un motto germanico. La figura di Pietro Abelardo, con il suo tormentato amore per Eloisa, le sue disavventure, i suoi scontri con i maestri legati al mondo dei monasteri e con le gerarchie della chiesa, il suo insegnamento brillante di una logica erede di quella greca ma nel contempo legata ai tempi nuovi, si presenta in un certo senso come emblema della nascita dell’università parigina.

La nascita delle università

Il nuovo fenomeno culturale non era limitato alla sola Francia. Qualche anno prima Irnerio aveva portato i libri legales, i codici del diritto romano, da Roma a Bologna, e qui ne aveva iniziato l’insegnamento. Tanto gli studenti quanto i docenti dovevano adeguarsi al clima sociale delle città basato sulla struttura delle corporazioni, le cosiddette universitates, in tutta Europa costrette a divincolarsi tra le gerarchie religiose e il potere politico, ma destinate a mutare la storia del pensiero e della civiltà.

Avevano uno spiccato carattere professionale: le tre facoltà maggiori erano giurisprudenza, medicina e teologia, e poi, propedeutica a queste, la facoltà di arti, nella quale veniva insegnato il quadrivio matematico (aritmetica, geometria, astronomia, musica) e il trivio (grammatica, retorica, logica). La matematica insegnata era poca, e comprendeva un po’ di Euclide e di aritmetica. Col tempo crebbe il ruolo dell’astrologia, destinata anche ad avere un posto importante nella medicina. Ma gli aspetti più interessanti della matematica nelle università concernevano il suo rapporto con la filosofia naturale.

Leonardo Fibonacci e Giordano Nemorario

Quello universitario era un insegnamento largamente indifferente alle tecniche, ma fuori delle università la rinascita economica creava in molte professioni una crescente domanda di matematica pratica ed erano i paesi di cultura islamica il luogo dove trovare le tecniche opportune. Non è quindi casuale che il primo vero matematico europeo provenga da una famiglia di mercanti pisani e la sua formazione si svolga sulle coste settentrionali dell’Africa all’inizio del xiii secolo.

È Leonardo da Pisa, detto il Fibonacci (1170 ca-1230), filius Bonacci, dal nome del padre. Il suo testo principale noto come Liber abaci, è dedicato all’algebra araba e ai temi classici della tradizione pratica, dagli algoritmi numerici alle applicazioni commerciali (con grande attenzione a dettagli quali le unità di misura nelle diverse città, le leghe metalliche ecc.). Anche lo stile, fondato su problemi, è nel solco di quella tradizione. Va comunque sottolineato come Fibonacci fosse un matematico raffinato, buon conoscitore anche di quella parte della tradizione teorica, Euclide innanzitutto, che era entrata già nella matematica araba. Occorre tuttavia fare qualche osservazione. In primo luogo, nel libro, nonostante il nome, non si usa mai l’abaco, ma sempre i nuovi algoritmi basati sulle cifre indoarabe. Succedeva lo stesso nelle cosiddette scuole d’abbaco, di cui si parlerà più avanti. Si conferma così come il termine abaco nel basso medioevo finisse col denotare in generale tutta la tradizione pratica, quella che in questo excursus è stata chiamata la matematica dell’abaco. Una seconda osservazione è che nel libro l’autore introduce le cifre da 1 a 9 come figure e lo 0 come semplice signum: nonostante lo zero fosse ormai usato negli algoritmi come le altre cifre, esso non appariva ancora esplicitamente come numero. Una terza osservazione è che Fibonacci frequentò la corte di Napoli di Federico ii negli stessi anni in cui il sovrano fondava l’università di Napoli anche con scopi pratici, ma non ci sono tracce di un rapporto tra Fibonacci e quella università. È il segno di una frattura che caratterizzò con pochissime eccezioni (soprattutto italiane) la storia della matematica medievale.

I numeri sono sempre definiti in modo usuale, come «somma» o «collezione» di unità, ma appaiono numeri negativi e anche irrazionali, e vengono usate le frazioni in maniera del tutto naturale, così come i rapporti tra quantità eterogenee (quasi inevitabili nei commerci, basti pensare al prezzo unitario), con una notazione anche molto particolare:

Ovviamente se tutte le B_i sono uguali a 10, si ottiene sostanzialmente la rappresentazione decimale, che però Fibonacci non usa. La funzionalità della sua notazione è evidente se si considera che le sottounità di misura all’epoca erano diverse da città a città e raramente decimali, così che quella di Fibonacci era una rappresentazione effettivamente più flessibile di quella decimale, ponendo le B_i uguali ai fattori di conversione tra le unità di misura e le A_i uguali alla misura data, scritta in tali unità. In algebra permane la duplicità tra una manipolazione sintattica e una risoluzione aritmogeometrica: se ne ha traccia nel fatto che l’incognita è detta cosa nella manipolazione algebrica del problema, è detta radice nella equazione da risolvere.

Fibonacci non è però l’unico protagonista della nascita della matematica in Europa nella prima metà del xiii secolo: va ricordato anche Giordano Nemorario (sec. xiii), probabilmente legato alla facoltà d’arti. In lui lo stile euclideo si dispiega sull’aritmetica, partendo dai libri aritmetici degli Elementi. Ma quelle proprietà algebriche che l’antica algebra geometrica concepiva in maniera esclusivamente geometrica cominciano a essere da lui trattate in maniera aritmetica e simbolica, con l’uso di lettere per indicare i numeri generici e parole come et, ductu, equalis per designare somme, prodotti ed equazioni. Si riconosce ancora dietro i simboli un significato geometrico nei passaggi, che hanno però frequentemente il carattere di una semplice manipolazione simbolica di proprietà aritmetiche.

Così per esempio il calcolo del quadrato del binomio, che nell’antichità si basava sulla costruzione geometrica delle figure 3 e 4, appare ora dedotto dalla proprietà distributiva e dal teorema: «Se un numero è diviso in due parti, allora quello che si ottiene dal prodotto del numero intero per una parte è quanto si ottiene dal prodotto della parte per sé stessa e per l’altra parte», cioè in formula moderna (a + b)a = a² + ab, a sua volta ricavato da un ragionamento puramente aritmetico.

Di Giordano Nemorario va ricordato anche lo studio matematico della statica, con la prima idea del principio dei lavori virtuali, dal quale inizia negli ambienti universitari europei quel rapporto tra matematica e fisica, inedito nella matematica greca, che sarà uno dei caratteri essenziali della scienza moderna.

Fibonacci e Giordano Nemorario presentano varie affinità di linguaggio nonostante avessero una estrazione sociale del tutto diversa: da un lato il mondo dei commerci, dall’altro quello delle università; il primo più attento alle applicazioni, il secondo più concentrato sullo stile dimostrativo. Saranno i secoli successivi, fino al rinascimento, ad approfondire la divaricazione fra questi due mondi e, dal punto di vista delle conoscenze e sulle scoperte, saranno secoli in cui la matematica sembrerà ristagnare.

Si devono così considerare per il basso medioevo due ambienti matematici separati: le professioni e le università. In quest’ultima le conoscenze e innovazioni matematiche sono estremamente limitate. Ma emergono due aspetti che risulteranno importantissimi: il ruolo della logica e del linguaggio da un lato, il rapporto con la filosofia naturale dall’altro.

L’università e la scolastica

L’importanza assegnata all’analisi dei testi linguistici è uno dei caratteri essenziali della cultura medievale, nella quale base della sapienza e del sapere non era la natura, ma un libro, anzi il libro, la Bibbia. Sino dai primi concili dell’antichità la disputa teologica si era basata sull’analisi logica dei testi. Il sapere degli antichi riguardava un mondo “visto e descritto”, per i medievali il sapere era soprattutto “scritto e interpretato”.

La logica aristotelica era pervenuta solo in parte ai dotti del medioevo soprattutto attraverso gli scritti di Boezio e di un tardo commentatore di Aristotele, Porfirio. Era stata sufficiente però a dare un’impronta caratteristica alle questioni teologiche dell’epoca. Si può a questo proposito ricordare la celebre prova ontologica dell’esistenza di Dio, dovuta ad Anselmo d’Aosta (1033 o 1034-1109). In essa si assume il punto di vista di un non credente, il quale, proprio in quanto non credente in Dio, deve avere nella mente l’idea di Dio, della quale aspetto essenziale è la perfezione. Ma l’idea di perfezione deve contenere quella di esistenza, in quanto una cosa esistente è più perfetta rispetto a una non esistente, così che anche il non credente deve in definitiva riconoscere la necessaria esistenza di Dio. I punti dubbi di questa prova costituiranno per secoli argomento di discussione basata sul concetto stesso di esistenza. Ma anche questo esempio mostra la differenza tra la logica medievale e quella aristotelica. Quest’ultima si fondava sul sillogismo, costruito a imitazione della relazione causale tra i fatti; nella logica medievale, invece, il fondamento è l’analisi dell’uso dei termini nel linguaggio, il quale assume un carattere più tecnico e convenzionale (altro effetto della natura multilinguistica della cultura dell’epoca) ed è anche più autonomo dalla realtà, che non deve semplicemente rispecchiare.

Occam e Buridano

La cultura che si trasmetteva nelle università medievali è nota con il nome di scolastica. Pur apparendo molto ostica alla sensibilità moderna, in essa emergono mutamenti cruciali sui temi del linguaggio e del carattere linguistico della scienza, la matematica in primo luogo.

La scienza per i greci riguardava, attraverso gli universali, direttamente la realtà ed era in questo un’immagine fedele del mondo, col linguaggio come tramite quasi naturale e non tematizzato. È Guglielmo di Occam (1280 ca-1349 ca) ad abbandonare questa connessione e a intuire come la scienza sia strutturata in proposizioni attraverso le quali descrivere il mondo. Sembra una tipica questione scolastica, ma da qui deriverà anche l’idea che la scienza non è semplicemente l’insieme di tutte le verità necessarie, ma piuttosto un processo in cui essa si costituisce come discorso intorno al mondo. Nella scienza antica una delle categorie con cui trattare le cose era la quantità, un sistema di attributi immanenti nel mondo e presenti nel linguaggio naturale come aggettivi: numeri e figure. Ma Occam si rende conto invece di come essi non siano necessari per descrivere il mondo; a tal fine bastano le cose stesse, le sostanze, e le loro caratteristiche, le qualità. Era una svolta traumatica poiché la matematica, che era stata nell’antichità il cuore dell’idea stessa di scienza, ne veniva estromessa.

L’idea che la scienza sia un linguaggio con cui parlare del mondo è un tema nuovo, che investe i successori di Occam. Tra questi Giovanni Buridano (1295 ca-1358 ca), che si pone il problema di trovare un linguaggio che sia non l’immagine del mondo, ma qualcosa di autonomo con cui si possa costruire una scienza che parta dall’esperienza e dalle conoscenze individuali per giungere tramite l’induzione alle conoscenze universali, una scienza che non si contrapponga più alle tecniche in quanto le sue verità non sono più necessarie e certe.

In questa analisi il linguaggio naturale viene letto in termini algebrici; l’individuo viene concepito come determinatum (Socrates, una costante) o vagum (hic homo, un’incognita o un segno, analogo alla cosa degli algebristi, singolo numero incognito), la cui vaghezza si dissipa tramite l’aggiunta delle condizioni del problema: l’individuo è caratterizzato ex circumlocutione come in Sophronisci filius. È la nuova connessione tra logica e algebra: la costante, l’incognita, l’equazione e la sua soluzione. Buridano insiste sul fatto che il segno possa avere un significato anche se non rappresenta una cosa esistente (come nei problemi che non ammettono soluzione), e si chiede se primus rex Franciae christianus individui univocamente, come ci si chiede se un’equazione abbia un’unica soluzione. Aristotele aveva interpretato il caso del bambino che chiama tutti gli uomini «padre» come conseguenza della mancanza in lui degli universali, Buridano lo interpreta come l’esistenza iniziale di un individuo vago (“un segno”) da cui derivano tanto gli individuali quanto gli universali.

Tipica della scrittura medievale era poi l’abitudine massiccia di abbreviare le parole con contrazioni, troncamenti, simboli sovrascritti o convenzionali. Una prassi, pressoché assente nel mondo islamico, che nasceva dal carattere meccanico della copiatura dei manoscritti e al tempo stesso dal carattere tecnico e strumentale del latino medievale e che sarà all’origine del simbolismo che caratterizzerà l’algebra europea: non solo le lettere, ma autentici nuovi simboli quali +, −, =, e successivamente i simboli per le potenze, per le radici ecc. E, come accade spesso nella storia della matematica, i simboli diventano cose, delle quali parla un linguaggio. Si assiste così lentamente alla trasformazione dell’algebra araba attraverso la linguistica e la scrittura medievale, e al lento emergere di un nuovo linguaggio algebrico dotato di una sua autonoma sintassi. Questo processo arriverà a compimento molto più tardi, nel xvii secolo, ma è il medioevo a predisporre l’universo linguistico: le radici dell’algebra simbolica si trovano nella scolastica.

Altro aspetto della logica scolastica che si rivelerà fertile per l’algebra moderna è l’attenzione a una ars inveniendi più che a una ars demonstrandi. Questa distinzione ricorda quella antica tra analisi e sintesi, ma viene posta in termini di argomentazione logica più che matematica: il sillogismo è la classica procedura per connettere il suo termine inferiore a quello superiore utilizzando il medio, ma se scopo della scienza è trovare tale connessione, allora, dati i due estremi, occorre trovare il medio. Inoltre, la logica medievale cominciava ad abbandonare l’idea che l’unica forma argomentativa fosse il sillogismo, così che l’«arte del trovare» iniziava ad assumere il carattere di un metodo scientifico generale.

Matematica e filosofia naturale

Concetti teorici tradizionalmente considerati come fisici, quali l’infinito o il continuo, cominciano a essere letti in linguaggio matematico.

In primo luogo occorre sottolineare come nel medioevo cada l’antica preclusione verso l’infinito attuale, per la semplice ragione che tutti gli attributi divini (giustizia, bontà, misericordia ecc.) sono «attualmente» infiniti. In altri termini, senza infinito non si può parlare di Dio. E inoltre la sua onnipotenza non può fermarsi di fronte alla creazione di oggetti infiniti.

Progressivamente questa novità teologica filtra anche nella filosofia naturale e nella matematica insegnate nell’università di Oxford, a cominciare da Roberto Grossatesta (1175-1253). Di carattere matematico è l’esempio della creazione di un oggetto infinito in un tempo finito: Dio potrebbe creare una quantità in mezz’ora, la stessa quantità nel successivo quarto d’ora, la stessa ancora nel successivo ottavo di ora ecc. e così dopo un’ora aver creato una quantità attualmente infinita. All’opposizione infinito attuale/potenziale si affiancherà poi l’idea di transfinito, «che eccede ogni finito al di là di ogni determinata proporzione», che esplicitamente rivela la traduzione matematica del problema e si pone come negazione del finito.

Tale lettura matematica dell’infinito si traduce in un problema nuovo e di grande portata per il futuro della matematica: il confronto tra infiniti. Gli infiniti sono tutti uguali? O esistono infiniti più grandi di altri infiniti? Su questo la scolastica si dividerà. Qui entravano in conflitto due principi fondamentali della matematica: uno di origine geometrica, «il tutto è maggiore della parte» (v assioma degli Elementi), l’altro di origine aritmetica: due moltitudini che si possono mettere in una corrispondenza biunivoca sono uguali.

Esistevano diversi paradossi in cui questi due principi entravano in conflitto. Paradossi sia aritmetici (i numeri interi e i numeri quadrati si possono mettere in corrispondenza biunivoca pur essendo i secondi una parte propria dei primi) sia geometrici: in un triangolo coi lati disuguali le parallele alla base istituiscono una corrispondenza biunivoca tra i punti dei due lati pur essendo il minore riducibile a una parte del maggiore, in due cerchi concentrici i raggi istituiscono una corrispondenza biunivoca tra i punti delle circonferenze (fig. 14).

La questione del continuo

Il problema dell’infinito era legato a quello del continuo. Infatti, se invece di aggiungere grandezze Dio avesse diviso un intervallo in mezz’ora, e poi i due intervalli ottenuti in un quarto d’ora e poi ancora i quattro intervalli in un ottavo d’ora ecc., in un’ora avrebbe potuto ridurre qualsiasi grandezza nei suoi punti, sfidando così l’antica preclusione aristotelica verso la costituzione di un intervallo tramite i suoi punti. Anche in questo caso la svolta veniva tanto dal pragmatismo della cultura medievale quanto dalla ormai piena liceità teologica dell’idea di infinito attuale, che porterà Cartesio ad affermare, nelle Meditationes de prima philosophia, qualche secolo più tardi: «Vedo manifestamente che si trova più realtà nella sostanza infinita che nella sostanza finita, e quindi che ho, in certo modo, in me prima la nozione dell’infinito che del finito, cioè prima la nozione di Dio che di me stesso».

Celebre il paradosso della rota Aristotelis (fig. 15), già noto a Erone: due cerchi solidali e concentrici rotolano finché la ruota esterna ha percorso un’intera circonferenza. I punti più bassi delle due ruote percorrono entrambi un intervallo uguale alla circonferenza maggiore, ritornando nelle stesse condizioni di partenza, pur essendo le circonferenze di diversa lunghezza.

Gli eventuali elementi ultimi che costituivano il continuo potevano essere omogenei (cioè intervalli per intervalli, superfici per superfici ecc.) secondo una tradizione vagamente atomista, o eterogenei (cioè punti per intervalli, intervalli per superfici ecc.) secondo una tradizione vagamente platonico-archimedea, in tal caso magari generabili dal moto di un indivisibile (un punto in moto genera la linea ecc.). La tesi atomista si scontrava con l’incommensurabilità, quella archimedea coi paradossi legati alla esistenza reale dei punti.

Su questi temi si nota il mutamento che il pensiero di Occam e Buridano impone alla matematica: svanisce il problema se i punti esistano o meno, poiché la scienza è fatta di proposizioni e i punti sono solo termini che possono entrare, magari come ipotesi, in determinate proposizioni, e questa loro esistenza ipotetica, secundum imaginationem, è sicuramente lecita. Anche perché, diversamente da altri enti solo immaginabili (come chimere e grifoni), tale esistenza è utile per la ragione.

I Calculatores

Sempre a Oxford, nel Merton College, lavora nella prima metà del xiv secolo un gruppo di filosofi (Thomas Bradwardine, William Heytesbury, Richard Swineshead), noti come Calculatores, ai quali si deve il tentativo di estendere il campo d’azione della quantità a quelle che la filosofia antica e medievale considerava qualità (non solo velocità, illuminazione, calore ecc., ma anche grazia, carità ecc.) e che il medioevo definiva intensive poiché potevano aumentare o diminuire di intensità.

L’esempio preferito era la velocità e ai Calculatores va ascritto quello che è noto come teorema mertoniano, secondo cui, in termini attuali, lo spazio percorso in un moto uniformemente accelerato è uguale a quello percorso nello stesso tempo in un moto uniforme a velocità media tra quella iniziale e finale.

Poco dopo, a Parigi, Nicola di Oresme (1325 ca- 1382) tradurrà questo teorema in una presentazione e giustificazione geometrica (fig. 16).

Bisogna però non confondere tale immagine con una rappresentazione cartesiana, in quanto non è una rappresentazione pur essendo una imaginatio. Infatti per Nicola di Oresme un calore “triangolare” punge più di uno “rettangolare”! La figura è fuori della realtà comune ma ha effetti reali. Inoltre l’ambiguità tra elementi eterogenei o omogenei fa sì che l’area venga vista sia come spazio percorso sia come velocità totale (in quanto una somma di velocità istantanee deve essere una velocità). L’aumento era inteso in termini di gradi discreti, anche se eventualmente infiniti. Questo è uno degli aspetti più caratteristici dello sviluppo della quantificazione medievale. Nei campi più diversi (il tempo degli orologi meccanici; la rappresentazione della musica tramite i neumi, gli antenati delle nostre note su uno spartito; la temperatura in termini di gradi; la velocità delle navi in termini di nodi) il medioevo quantificava discretizzando le qualità intensive anche se le presentava come intervalli, latitudines, cioè come grandezze continue.

Tuttavia la stranezza si attenua se si ricorda che tutti i modi per esprimere una quantità, che fossero numeri o semplici parole, erano discreti, in quanto non si conoscevano ancora i numeri reali, e la distinzione tra discreto e continuo era nebulosa nella tradizione pratica, ancora dominante, sebbene ciò si sovrapponesse a una struttura teorica aristotelica che quella distinzione invece riteneva netta. Per questo motivo la misurazione era solo formale, era una quantificazione discreta, ma intuita geometricamente e senza misura empirica.

La fine del medioevo

Anche se nelle università era filtrato poco della nuova matematica degli arabi (solo i rudimenti sugli algoritmi numerici), la riflessione sulla scienza e sul linguaggio aveva posto il problema della collocazione stessa della matematica all’interno del sapere. Fuori delle università, invece, la nuova matematica investiva il tumultuoso sviluppo della società e dell’economia tardomedievale. I commercianti, gli artigiani, gli architetti, i pittori, si rivolgevano alla matematica degli arabi per le esigenze delle loro professioni. Soprattutto in Italia, ma anche in Germania, la nascita dei comuni aveva accelerato lo sviluppo di tali professioni e la crescente domanda di conoscenze matematiche si era tradotta nella nascita delle scuole d’abbaco, talora organizzate dai comuni o dalle corporazioni, talora a opera di iniziative private. Tali scuole d’abbaco (nelle quali non vi era traccia di veri abaci) appaiono verso la seconda metà del xiii secolo nell’Italia centro-settentrionale, a Firenze soprattutto, e fioriscono sino all’inizio del xvi secolo. Costituiscono l’istruzione superiore che conduce a un diffuso processo di formazione: Giovanni Villani ci informa che a Firenze intorno al 1330 c’erano da otto a diecimila giovani che frequentavano le scuole elementari pubbliche e circa 1000-1200 che, dopo gli undici anni, imparavano «l’abbaco e algorismo» per due o tre anni, e che era normale per un artigiano saper leggere e far di conto.

L’insegnamento da parte dei maestri d’abbaco era in volgare e all’inizio puramente orale. Successivamente apparvero i «trattati d’abbaco», nei quali era raccolto un programma tutto interno alla tradizione pratica, ma che non sembra derivare dal Liber abaci di Fibonacci. Questi trattati diventeranno col tempo più completi e rigorosi e in essi si cimenteranno anche artisti come Piero della Francesca. Una tendenza che culminerà con l’opera di Luca Pacioli (1446-1517), il cui sodalizio con Leonardo da Vinci, «omo sanza lettere» ma attento lettore di matematica, è paradigmatico del rapporto inedito che si stringe tra matematici pratici e grandi artisti del rinascimento, con interessi anche meccanici e matematici. Quasi emblematica di questa connessione è la teoria della prospettiva, che nasce nella forma di regole pratiche per dare il senso della profondità nella pittura, ma che presto diviene una precisa tecnica matematica da cui si svilupperà la geometria proiettiva.

Nel rinascimento la tradizione pratica ancora dominante diventa strettamente algoritmica e la conoscenza degli algoritmi assume quel carattere mnemonico che tutto sommato caratterizza ancora oggi l’insegnamento della matematica elementare. Nell’antichità la memorizzazione delle procedure si appoggiava probabilmente su esempi numerici e figure geometriche, nel rinascimento esse vengono memorizzate più astrattamente e verbalmente; in seguito assumeranno anche l’aspetto di formule. Gli algoritmi non vanno compresi, vanno memorizzati: per esempio le tabelline pitagoriche, la regola del tre, la prova del nove, o l’estrazione della radice quadrata.

Nicola Cusano

È difficile alla fine del medioevo ritrovare qualche legame tra la matematica delle università e quella delle scuole d’abbaco, soprattutto in Inghilterra e Francia, laddove, anche a causa della guerra dei cent’anni, le università avevano perso il dinamismo che le aveva caratterizzate nel xiii e xiv secolo.

In Italia e Germania la situazione era migliore. A tale proposito va menzionato il cardinale tedesco Nicola Cusano (1400 o 1401-1464), una figura importante, quasi una cerniera tra medioevo e tempi moderni. Per quanto riguarda la matematica, il suo nome va ricordato per aver fatto delle sue riflessioni sull’infinito il grimaldello per rompere lo schema delle opposizioni aristoteliche. Moto e quiete erano opposti per Aristotele, ma un infinito rallentamento del moto è la quiete; analogamente retta e curva erano opposti, ma la retta poteva essere considerata come una circonferenza di raggio infinito. In Cusano si trova anche un’idea che si diffonderà nei secoli successivi, diventando un luogo comune nel Seicento: che sia la matematica e non la logica la base della argomentazione scientifica. Nel Cinquecento gli aristotelici sottolineavano i limiti della dimostrazione matematica (estranea alla causalità fisica, non univoca, non sillogistica) al punto da escludere la matematica dalle scienze. I platonici e i meccanici, Leonardo da Vinci per primo, trovano invece nella matematica la logica delle loro macchine e lo strumento base per tutte le scienze. Prendeva le mosse un lungo dibattito su quale fosse tra le due la dimostrazione principale, se quella logica o quella matematica; di fatto, la logica si avviava a un lungo periodo di stasi, interrotto prima dell’Ottocento solo dalla figura di Leibniz.

L’invenzione della stampa e il fiorire delle traduzioni

Con l’invenzione della stampa intorno alla metà del xv secolo, il libro, anche il libro di matematica, usciva dall’angusto mercato dei copisti universitari per diventare un bene relativamente di massa: nel giro di pochi decenni le stamperie si moltiplicarono in Italia, in Germania, in Olanda, e i libri comparvero in tutte le case delle famiglie benestanti.

L’attenzione degli umanisti per le lingue antiche aveva lasciato in eredità anche una maggiore attenzione al rigore delle traduzioni, così che il Cinquecento vide un fiorire di nuove traduzioni dei classici della matematica greca. Tra i matematici più attivi nella diffusione del libro matematico c’era Johann Müller, detto Regiomontano (1436-76), famoso anche per i suoi studi di astronomia e trigonometria. Con lui inizia una tradizione di studi astronomici nella Mitteleuropa che porterà ai risultati di Copernico, Tycho Brahe e Keplero.

Il rinascimento è anche caratterizzato dall’esplicito interrogarsi sul linguaggio, in una civiltà ormai largamente multilinguistica: si erano formate le lingue nazionali, si traduceva da una lingua europea all’altra oltre che dall’arabo, dal greco, dal latino e dall’ebraico. I linguaggi apparivano tutti convenzionali ma, quasi per contrappeso, nasceva l’esigenza di un linguaggio universale, in cui le cose avessero il loro vero nome. Poteva essere il linguaggio originario, quello di Adamo, simile all’ebraico, o un linguaggio iconico, come il cinese proposto da Leibniz; un linguaggio da riscoprire o anche da creare. Era un’indagine impensabile nella Grecia antica, in cui il greco era l’unico idioma che non fosse un balbettio, o nell’Islam, laddove l’arabo era l’unica lingua vera e immutabile, quella in cui era scritto il Corano.

L’età moderna
L’algebra del Cinquecento

In Italia appaiono le novità più rilevanti in campo matematico, soprattutto in algebra. L’algebra in Europa aveva progressivamente costruito un ricco lessico simbolico e sviluppato ampie possibilità di manipolazione delle espressioni. Andava crescendo la consapevolezza che i risultati dell’algebra geometrica potevano essere ottenuti tramite la manipolazione di espressioni, e in questo gli algebristi italiani del Cinquecento avevano raggiunto un indiscutibile primato. Ciononostante l’algebra era ancora essenzialmente una disciplina della tradizione pratica, rivolta quasi esclusivamente alla risoluzione di problemi. In particolare, i problemi che portavano a equazioni di grado superiore al secondo solo raramente erano risolvibili in quanto non esistevano procedure generali.

L’ambiente matematico appariva poco strutturato: qualche collegamento con le università, incarichi all’interno delle corti, legati al ruolo che i matematici svolgevano come meccanici e ingegneri nelle soluzioni concrete di problemi bellici, idraulici o architettonici. Vi era una grande attenzione verso gli scritti di Archimede, e si diffondeva l’idea di una meccanica come scientia media tra geometria e fisica, ma nel contempo anche autonoma. La matematica era molto richiesta per l’astrologia, che si diffondeva in tutti gli strati della popolazione, curia e corti incluse. Esisteva una diffusa e aspra concorrenzialità tra i matematici, che si traduceva in autentici «cartelli di sfida» in cui un matematico sfidava altri matematici a risolvere problemi, e la storia della scoperta della risoluzione delle equazioni di terzo grado mostra il clima acceso che circondava tali sfide.

Scipione Dal Ferro (1465-1526) per primo trovò tale soluzione all’inizio del xvi secolo, ma la tenne segreta. Niccolò Tartaglia (1499-1557) forse la riscoprì da solo e la confidò poi a Girolamo Cardano (1501-76) con l’impegno a non divulgarla. Ma Cardano venne a sapere che il primo scopritore era stato Scipione Dal Ferro e pubblicò la risoluzione ritenendosi sciolto dal vincolo di segretezza; ne seguì una ferocissima polemica.

Anche se qui per semplicità è utilizzato il linguaggio algebrico che Cartesio introdusse un secolo dopo, nella manipolazione algebrica era ancora dominante l’uso del linguaggio naturale: Tartaglia descrisse con una poesia la soluzione dell’equazione

(era già noto come eliminare il termine di secondo grado tramite una opportuna sostituzione x′ = x + a). La soluzione si fonda su una costruzione geometrica (fig. 17).

Si considera il cubo di lato x = AB, si “completa” il solido nella forma di un cubo di lato u = AC, in modo che i tre parallelepipedi di lati x, u, e v = u − x = BC diano un volume px, cioè 3xuv = px, e quindi uv = p/3. La somma di tale volume e del cubo di lato AB vale quindi q e risulta uguale, con semplici ragionamenti di natura geometrica, alla differenza tra i volumi del cubo di lato AC e del cubo di lato BC:

Sostituendo u = p/3ν si ottiene una equazione di secondo grado in ν ³:

Da qui è possibile calcolare ν ³, ν, u e quindi x.

È molto difficile capire se questa soluzione fu trovata tramite un ragionamento geometrico o algebrico, se cioè il completamento del cubo fu realizzato sulla figura o tramite la formula del cubo del binomio (come nella nostra traduzione algebrica). L’equivalenza dei due linguaggi all’epoca non era ancora esplicita, ma intuitivamente era già diffusa anche tra non matematici.

Tuttavia quello geometrico doveva in ogni caso essere il senso generale della soluzione, come si evince dal fatto che ancora per tutto il secolo si darà non un’unica ma diverse risolventi, poiché le grandezze coinvolte dovevano essere sempre positive in quanto rappresentanti grandezze geometriche: nell’Algebra di Bombelli appaiono cinque casi per la risoluzione dell’equazione di secondo grado, 16 per l’equazione di terzo grado e ben 42 per l’equazione di quarto!

D’altra parte, la scoperta della soluzione per l’equazione di quarto grado (impensabile in un approccio puramente geometrico) da parte di Ludovico Ferrari (1522-65), un allievo di Cardano, testimonia la raffinatezza delle tecniche di manipolazione simbolica. Infatti, nella procedura di risoluzione occorre porre a un certo punto un intervallo uguale al quadrato di un altro intervallo, ignorando il principio di omogeneità dimensionale: qualcosa di lecito nell’antica tradizione aritmogeometrica, ma geometricamente inaccettabile. Tuttavia alla metà del xvi secolo stava ormai maturando una matematica del tutto nuova che in un certo senso saldava le due antiche tradizioni, teorica e pratica. È qualcosa che si intravede già nell’opera dell’ultimo grande algebrista italiano del xvi secolo, Raffaele Bombelli (1526-1572?), nel quale linguaggio algebrico e geometrico appaiono interscambiabili con la massima naturalezza. Parlando di aritmetica e geometria egli scrive: «Queste due scientie hanno intra di loro tanta convenientia che l’una è la prova dell’altra e l’altra la demostration dell’una», e dimostra le risolventi delle equazioni secondo una pluralità di approcci, geometrici e aritmetici. Bombelli analizza i diversi modi di intendere la risoluzione di un’equazione, quasi un sunto di storia dell’algebra. Per esempio, l’equazione di primo grado ax = b viene risolta in tre modi. Nel primo (fig. 18), in originale senza i cerchietti, «in superficie composto di numero», b è una superficie, x e a sono lunghezze (viene preservato il principio di omogeneità), ƒ è l’unità di misura e a è un numero esplicitamente dato (nell’esempio, 2). I due rettangoli devono avere la stessa area, ragion per cui x si trova numericamente dividendo b per a: vi si puo riconoscere la tradizione pratica aritmogeometrica. La seconda soluzione (fig. 18) «in superficie senza numero»: b è un rettangolo dato, la cui base viene prolungata di a. Completando la figura si ottiene x come grandezza geometrica non metrica, in quanto i due rettangoli opposti alla diagonale hanno la stessa area b, in base al teorema vi.14 degli Elementi, quindi nella forma integralmente geometrica della tradizione teorica. La terza soluzione «in linea» (fig. 18), cartesiana ante litteram, abbandona il principio di omogeneità, b e a diventano lunghezze e ƒ è l’intervallo unitario; a : b = 1 : x e di qui si calcola x: qui si vede all’opera una concezione post-euclidea e un uso algebrico della teoria delle proporzioni. L’introduzione del segmento unitario ƒ appare teoricamente all’inizio del quarto libro dell’Algebra di Bombelli, laddove l’autore applica le operazioni aritmetiche alle linee e in cui accetta anche linee negative, ma la sua caratterizzazione transdimensionale (trattabile come numero, segmento, quadrato ecc.) appare già all’inizio del libro. Il principio di omogeneità, secondo il quale in una equazione tutti i termini devono essere dimensionalmente omogenei, assente nella tradizione pratica e centrale in quella teorica, è disinnescato dall’uso del «segmento unitario», la «comune misura», così che si può tracciare una linea prodotto di due linee. Così Bombelli, anche se in modo euristico e non sistematico, costruisce quella corrispondenza tra operazioni algebriche e geometriche che sarà fondamentale in Cartesio.

La nascita della scienza moderna

All’alba della nuova scienza, si può fare un confronto tra la matematica europea e quella araba per rispondere a quello che è il più grande interrogativo della storia della scienza: perché in Europa? Perché la scienza moderna nasce qui e non in Cina o nell’Islam?

Limitandoci al solo confronto con la scienza islamica, e considerando i soli aspetti scientifici, si deve osservare come la matematica islamica appaia a prima vista aver fatto passi avanti nella direzione della scienza moderna anche più decisivi di quella europea: nella matematica islamica risulta più chiara ed esplicita la confluenza di continuo e discreto e la riduzione del rapporto a numero, nonché più avanzato lo sviluppo delle tecniche algebriche sintattiche (anche se senza un nuovo simbolismo). Anche nelle scienze «medie», dall’astronomia all’ottica, i progressi appaiono più significativi, e più sviluppate appaiono anche le tecniche alchimistiche e la strumentazione astronomica.

La matematica europea, dopo l’improvvisa fioritura legata ai nomi di Fibonacci e Giordano Nemorario, appare invece ancora dominata dalla frattura tra una matematica universitaria antiquata, e una matematica d’abaco grossolana. Certo si riscontrano fenomeni positivi nell’uso della matematica su temi fisici da un lato, e su questioni tecniche e professionali dall’altro. Ma niente di rilevante: ancora all’inizio del Cinquecento l’unico settore scientifico ben caratterizzato della matematica europea era l’astrologia. Eppure nella matematica del tardo medioevo si preparano i caratteri di una svolta epocale. Nicola di Oresme, l’ultimo dei grandi scolastici del xiv secolo, si inventa un dialogo tra Aritmetica e Geometria presenziato da Apollo. Da un lato l’aritmetica esalta la commensurabilità per il piacere che procura in musica, per l’utilità che rivela nella costruzione delle tavole astronomiche e per la conoscenza esatta, dall’altro la Geometria difende invece (con il plauso di Nicola di Oresme) l’incommensurabilità, che garantirebbe una grande varietà di effetti in musica, sebbene richieda di doversi accontentare di approssimazioni. E si pone il problema, rilevante perché funzionale a questioni astrologiche, se i tempi di percorrenza delle orbite planetarie siano commensurabili o no, osservando (molto modernamente) che la probabilità che siano commensurabili è molto bassa e intuendo così come gli irrazionali siano molto più numerosi dei razionali. La modernità di Nicola di Oresme appare anche nella capacità di usare argomenti matematici per problemi fisici, anche se la questione rivela ai nostri occhi un’impostazione abbastanza arcaica per quanto riguarda il confronto tra una proposizione matematica e una empirica: si ignora che la prima può parlare di uguaglianza in senso stretto, mentre la seconda solo di uguaglianza a meno di errori nelle osservazioni e misurazioni, inevitabili e imprevedibili.

Si intravede qui la difficile transizione verso la matematica e la scienza nella rivoluzione scientifica. Viene infatti da chiedersi “dove” fosse la matematica nell’antichità e nel medioevo. In realtà era immanente, era un tutt’uno con la superficie del mondo, era un frammento del linguaggio naturale: per Platone era un mondo di idee che apparivano nelle cose, per Aristotele veniva astratta dalla realtà, in primo luogo eliminando la materia e il moto. Aveva poi un ruolo cruciale nelle catene causali e quindi era la base della scienza e, se non era solo un insieme di tecniche, riguardava esclusivamente la verità necessaria e l’essere immutabile. I filosofi naturali del medioevo avevano cominciato a scorgere la matematica anche nel movimento: sarà Cusano a descrivere una curva nel moto di un punto su una ruota che rotola, e Brahe a ravvisare nei cieli non più sfere fisse ma traiettorie di corpi in moto. Nicola di Oresme arrivava addirittura a geometrizzare qualità fisiche come la velocità, la temperatura ecc., con la imaginatione. Tuttavia esse restavano sempre immanenti anche se non normalmente percepite. Quindi i tempi di rivoluzione planetaria erano ancora, come attributi, grandezze precise, i cui rapporti dovevano essere, per il principio del terzo escluso, commensurabili o incommensurabili.

Del tutto diverso è il luogo della matematica per la scienza moderna: essa scomparirà dalla realtà immanente, si collocherà nelle leggi fisico-matematiche di una realtà nascosta e profonda, nelle innumerevoli relazioni causali che spiegano il divenire di ogni evento nel mondo reale e che, per sommarsi negli effetti, dovranno assumere un carattere numerico. Questa matematica non appare nel mondo della vita quotidiana, richiede un linguaggio autonomo per essere descritta e non tratta più di numeri interi e figure, quanto invece di simboli algebrici, derivate e integrali, serie e limiti, numeri reali, infiniti e infinitesimi, termini di una realtà che nella vita quotidiana semplicemente non esiste. La scienza non sarà più un sistema stabile di verità riguardanti le sostanze e i loro attributi, ma diventerà un sistema per rispondere a problemi relativi alle relazioni tra grandezze osservabili, diventerà un metodo: un’idea che serpeggia già nel Cinquecento e che poi verrà definita da Cartesio. Tre secoli dopo Hilbert sosterrà che fin quando esisteranno problemi matematici la matematica sarà una scienza viva.

Ogni fenomeno reale sarà l’effetto di numerosissime relazioni causali scritte in forma algebrica e la cui misura è possibile esclusivamente in laboratorio: solo in un ambiente artificiale si può dipanare la matassa delle innumerevoli leggi naturali che regolano la realtà, isolandole. È questa la distanza tra l’antica esperienza (naturale e qualitativa) e il moderno esperimento (artificiale e quantitativo). Ed è questa la stessa logica che sovrintende all’idea di macchina, anch’essa luogo artificiale in cui si cerca di semplificare il sistema delle cause (eliminando gli attriti, misurando esattamente le dimensioni, garantendo l’invarianza delle condizioni e dei materiali ecc.) per ottenere tutti e soli gli effetti voluti. La matematica non è più aderente alle cose sulla superficie del mondo, come aveva intuito Occam, ma giace nella sua penombra, solo indirettamente e approssimativamente percepibile e utilizzabile, e per questo non avrà più senso chiedersi se il rapporto tra i periodi di rivoluzione dei pianeti sia commensurabile o no. La nuova dislocazione della matematica avrà effetti epocali: gli stessi aspetti estetici della musica, che fino al Seicento hanno carattere matematico e oggettivo, entro il Settecento saranno ormai del tutto qualitativi e soggettivi, mentre la matematica sarà solo nelle equazioni differenziali, presentandosi come la «forma impercepibile» delle leggi fisiche delle onde sonore.

È questo sottile mutamento a rendere possibile la nascita di una teoria della probabilità, una «scienza del caso» che apparirà quasi all’improvviso verso la metà del Seicento in autori quali Fermat, Pascal, Huygens. Infatti in un mondo di catene causali deterministiche il caso è solo una mancanza soggettiva di conoscenza, e dell’ignoranza non può esservi una scienza. Ma in un mondo dove ogni evento è risultato di innumerevoli causalità naturali i cui effetti si sommano e in cui la scienza può solo cercare di isolarne alcune per prevederne il divenire, si può costruire una scienza degli effetti minori trascurati e imprevedibili, degli innumerevoli «mondi possibili» che in ogni istante si aprono davanti al presente. La transizione fra queste due diverse collocazioni della matematica domina i primi secoli dell’era moderna, l’alba della rivoluzione scientifica.

La rivoluzione scientifica

La rivoluzione scientifica è un processo articolato, ma spesso è sommariamente descritta nei libri di storia della scienza come il generico prodotto di una concomitanza di diversi fattori sociali, economici, tecnologici, culturali, filosofici e religiosi. C’è invece un filo rosso che la percorre tutta, e tale filo è proprio il nuovo luogo della matematica, descritto precedentemente. Il centro di questa nuova collocazione è la meccanica, anzi, l’idea stessa di macchina (e di esperimento) è al centro della riflessione per tutto il Seicento.

Oggi nei libri la meccanica è parte della fisica, anzi la prima parte di essa, ma agli albori della scienza moderna essa era una disciplina speciale, non solo una scientia media, intermedia tra matematica e fisica (che restava ancora sostanzialmente qualitativa), come l’astronomia e la musica, ma anche il terreno di una mediazione inedita tra scienza e tecnica. Fino alla metà del Settecento non compare alcuna frattura tra fisica-matematica e filosofia: Galileo vorrà essere nominato «primo filosofo e matematico», il capolavoro di Isaac Newton (1642-1727) saranno i Philosophiae naturalis principia mathematica, che il recensore sul «Journal des sçavans» definirà «un’opera di meccanica ma non di fisica» (cioè filosofia naturale), osservando come lo studio newtoniano delle forze fosse matematico e l’attrazione provenisse da un punto inesistente nella realtà e non da un corpo reale. A dire il vero, alla base delle leggi fisiche in forma matematica ci saranno praticamente sempre princìpi di natura metafisica e teologica, da Cartesio e Keplero a Leibniz e Newton, in fondo anche in “meccanici” come Galileo e Huygens.

Soprattutto va sottolineata la totale affinità tra matematica e realtà e l’assoluta continuità tra meccanica e geometria; per Newton: «il metodo è derivato immediatamente dalla natura stessa», fluenti e flussioni «avevano luogo nella realtà della natura fisica» e quella geometrica non è una rappresentazione, ma una immagine immediata e fedele di una realtà solo in parte percepibile per via non artificiale e non esprimibile che geometricamente. Per Newton la meccanica non è più una scienza mista subordinata alla geometria, ma è la geometria a costituire una forma di meccanica, in quanto la prima si attua tramite le operazioni meccaniche di tracciare linee e costruire figure e la seconda in più ha il tracciamento di forze e moti.

Galileo Galilei

Il padre della scienza moderna, tra la fine del xvi e l’inizio del xvii secolo, è giustamente considerato Galileo Galilei (1564-1642), della cui opera si vuole qui sottolineare soprattutto il ruolo della matematica. «La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi agli occhi (io dico l’universo), ma non si può intendere se prima non s’impara a intendere la lingua, e conoscer i caratteri, ne’ quali è scritto. Egli e scritto in lingua matematica, e i caratteri son triangoli, cerchi e altre figure geometriche [...]». L’universo è un libro matematico, e quello che vi è scritto in caratteri geometrici è la filosofia naturale: Galileo non dice che l’universo è «descritto matematicamente» nel libro (della scienza) o che le leggi naturali dell’universo «sono scritte matematicamente» in un libro. La geometria, la meccanica e l’universo sono omogenei come i caratteri, il testo e il libro. La matematica di Galileo è quindi ancora sostanzialmente immanente, ma gli enti matematici non sono più gli attributi reali e immediati delle cose, sono invece la descrizione geometrica della realtà ignota, di cui la realtà immediata comincia a essere ormai solo la manifestazione qualitativa: il peso è il fenomeno di una gravità sulla cui natura Galileo non si pronuncia, ma della quale descrive la struttura matematica. Le differenze tra matematica e realtà non sono più dovute alla presenza della materia e del moto che inquinano le forme geometriche dell’essere, ma al fatto che diversi aspetti geometrici descrivono diverse causalità e la realtà percepita ne è la somma. I pianeti allora, con tutte le loro irregolarità mostrate dal telescopio, sono corpi geometrici a tutti gli effetti, quanto la più perfetta delle sfere.

Del libro dell’universo è parte essenziale la continuità del moto, forse il problema matematico più evidente in Galileo. Osservando i caratteri matematici del moto di un grave lanciato verso l’alto, è evidente che a un certo punto esso si ferma e poi comincia a cadere. Per quanto tempo si ferma? Per un solo istante? E nell’istante successivo alla quiete con che velocità si muove? Galileo intuisce che nel frenare e nell’accelerare il grave passa per tutti i gradi di velocità. È questa l’idea cruciale, più che la legge del moto per cui lo spazio percorso dal grave cresce col quadrato del tempo. Occorre ricordare che Galileo non conosce il numero reale e alle spalle ha una tradizione in cui la velocità cresceva di un gradus alla volta. Lo zero non esiste, al suo posto c’è il non gradus, ma non è solo un problema di termini; semplicemente non c’è un numero zero che separi i positivi dai negativi, come un punto su una retta la divide in due semirette. Galileo illustra il problema con un diagramma (a sinistra in fig. 19) su cui è rappresentato un intervallo [ns] che si muove nella direzione della freccia sino ad annullarsi nel vertice a, che si presenta come una sorta di limite, passando con continuità per tutti i valori intermedi. Il caso illustrato a destra nella fig. 19 in Galileo non esiste, non può esistere: in essa a sarebbe lo 0 che divide positivi e negativi. Quello che Galileo concepisce è una sorta di processo di rallentamento al limite dalle grandezze finite (di grado in grado?) fino al non gradus. Qualcosa di simile lo si ritrova anche in Stevin e Newton.

Il problema del continuo ricorre spesso in Galileo con i suoi classici paradossi. Per esempio nella rota Aristotelis (fig. 15) Galileo immagina di sostituire i due cerchi con due poligoni con un numero crescente di lati. Nella fig. 20 si vede come il poligono grande rotolando disegna una linea continua, quello piccolo una tratteggiata. Aumentando il numero di lati i “pieni” e i “vuoti” della tratteggiata diventano sempre più piccoli. E all’infinito? Si avranno infiniti lati e infiniti vuoti, tutti senza estensione come punti. Il continuo allora assume l’aspetto di un alternarsi di pieni e vuoti. E questa di Galileo è l’unica caratterizzazione geometrica non intuitiva del concetto di continuità che si trova nella storia della matematica: nell’antichità il concetto era fisico e qualitativo, nell’era moderna esso diventa un concetto aritmetico.

Il continuo aritmetico

Il continuo aritmetico appare proprio in quegli stessi anni con il concetto di numero reale, un’idea che era stata impensabile fino a pochi decenni prima e che rapidamente diventa tanto ovvia che nessuno si preoccuperà più di definirla fino all’Ottocento.

In questo quadro spicca Simon Stevin (1548-1620), tipica figura di quest’epoca di transizione tra Cinquecento e Seicento. Ingegnere e matematico, come tanti protagonisti della storia della matematica di questi anni, in cui la matematica pratica si sovrappone alle nuove questioni teoriche. Altri personaggi con analogo profilo (Bürgi, Nepero) in quegli stessi anni avevano tabulato le funzioni trigonometriche e introdotto (e tabulato) i logaritmi per facilitarne le operazioni. Questa pratica aveva reso familiari agli uomini dell’epoca numeri indefinitamente lunghi in quanto quelle tavole, diventando sempre più precise, utilizzavano un numero crescente di cifre significative. Erano in genere approssimazioni e l’uso pratico di rapporti irrazionali aveva reso coscienti che esistevano grandezze la cui misura numerica esatta non si poteva esprimere finitamente, ma la cui approssimazione numerica si poteva dare con qualsiasi precisione desiderata. A questo punto Stevin introduce la notazione decimale potenzialmente illimitata, praticamente la stessa che usiamo oggi.

Ma l’aspetto cruciale è che questa innovazione nella notazione si affianca alla intuizione del continuo numerico e alla completa scomparsa della opposizione tra continuo e discreto. Descrive Stevin ne L’arithmetique «la comunanza e similarità […] quasi identità» tra grandezza e numero: «A una grandezza continua corrisponde il numero continuo che gli è assegnato […] il numero è per la grandezza come l’umidità per l’acqua: penetra come questa in ogni parte dell’acqua; e come a una acqua continua corrisponde una continua umidità, così a un numero continuo corrisponde una grandezza continua».

Gli algebristi francesi

Nel Seicento muta anche il sistema delle istituzioni scientifiche: tramontano le scuole d’abaco e le università diventano sempre più ininfluenti (Galileo e Newton insegnano all’università all’inizio della loro carriera ma abbandonano poi il mondo accademico per altri incarichi). Il dibattito culturale si trasferisce nelle Accademie che fioriscono ovunque nel Seicento, punta dell’iceberg di intensi scambi epistolari tra i principali uomini di scienza.

All’inizio del secolo appare in Francia una novità che riguarda il rapporto tra algebra e geometria. François Viète (1540-1603), Pierre de Fermat (1601-65) e Renato Cartesio (nome umanistico italianizzato di René Descartes; 1596-1650) hanno radici culturali del tutto diverse dagli algebristi italiani. Questi ultimi avevano una formazione matematica e meccanica, spesso pratica, e talora erano collegati a facoltà come medicina. I francesi invece hanno una formazione giuridico-retorica e filosofica, e sono amateurs della matematica.

Il bagaglio tecnico da cui partono italiani e francesi non è molto diverso, ma c’è tra di essi una grande differenza: la notazione algebrica degli italiani si trasforma nei francesi in un linguaggio algebrico. Per la prima volta nella storia la matematica si dota di un suo autonomo linguaggio simbolico (la costruzione geometrica era stata solo una presentazione iconica). È interessante analizzare come cambia l’espressione di una equazione dalla metà del Cinquecento alla Géométrie di Cartesio (1637). Erano già comuni i simboli per le operazioni aritmetiche, in aggiunta Bombelli scriveva un’equazione come

Viète invece scrive

«aggiungere Z a A piano / B, la somma sarà

Cartesio infine scriverà:

Bombelli ha una notazione in cui può esprimere i polinomi (∪ è la incognita) e poi una parola («agguagliasi… a…») per indicare l’equazione. Viète estende la notazione per gli attributi dei termini («piano» esprime che la grandezza A è bidimensionale) e utilizza lettere tanto per le costanti quanto per le incognite, ma è Cartesio a fare della equazione una proposizione in un nuovo linguaggio totalmente simbolico (∝ è il segno di uguaglianza).

Cambia anche il ruolo della x, la cosa degli algebristi rinascimentali. Per questi ultimi essa era ancora semplicemente la grandezza incognita, tra gli algebristi francesi essa diventa anche la grandezza generica, con cui rappresentare curve e luoghi geometrici. E infine, considerando le curve tracciate da un punto in moto, diventerà anche la grandezza variabile, come il tempo e le altre grandezze fisiche. È sempre più evidente l’isomorfismo tra l’algebra geometrica e quella simbolica. In Viète domina l’equivalenza tra diversi linguaggi: quello geometrico, quello algebrico, quello meccanico, quello delle proporzioni, senza una gerarchia.

In seguito apparirà sempre più netta la centralità di quello simbolico, che è evidente anche nello sviluppo del concetto di numero: il numero reale, già apparso nella generalizzazione degli algoritmi numerici e nella notazione decimale di Stevin. Ora il simbolo algebrico, da Diofanto considerato un simbolo aritmetico, rappresenta una grandezza e il numero reale appare quindi anche come soluzione delle equazioni. Ma alcune equazioni mostrano soluzioni formali che non paiono grandezze. In primo luogo si trovano soluzioni negative, poi soprattutto, con l’autonomizzarsi delle tecniche di manipolazione algebrica, appare anche l’idea di numero immaginario. Questa estensione si lega all’intuizione, che verrà dimostrata successivamente da Gauss, che una equazione di n-esimo grado ammetta n radici, anche se non tutte distinte. Ma esistevano invece equazioni di secondo grado senza soluzioni reali o di terzo con una sola soluzione, e già Bombelli era riuscito a trovare soluzioni immaginarie usando come oggetto puramente formale √(−1), l’unità immaginaria che verrà poi indicata con i, per formare i numeri complessi, ottenuti come somma formale di un numero reale e di uno immaginario: a + ib. E soprattutto emerge la possibilità di trovare soluzioni reali manipolando soluzioni di equazioni di terzo grado che dall’algoritmo apparivano complesse. Infatti l’equazione x ³ = bx + c ammetteva come soluzione:

nella quale, per (c /2)² < (b /3)³, compaiono due numeri complessi perché radici quadrate di numeri negativi. Bombelli scoprì che dalla manipolazione algebrica della soluzione complessa si otteneva una soluzione reale, e questo in un certo senso mostrava una sorta di omogeneità algoritmica tra numeri complessi e numeri reali.

Gli algebristi francesi in realtà preferivano definirsi analisti, poiché si richiamavano all’analisi (in contrapposizione alla sintesi) di cui si è parlato a proposito della matematica greca. Addirittura essi consideravano i loro lavori come la riscoperta di tecniche analitiche tenute nascoste dai loro antichi ideatori. Ma in realtà nel Seicento l’antica coppia analisi/sintesi si sovrappone da un lato alla distinzione di origine aristotelica tra composizione (procedere dall’universale al particolare, secondo l’ordine naturale) e risoluzione (procedere dal particolare all’universale, secondo l’ordine della conoscenza), dall’altro all’alternativa tra algebra simbolica e geometria. L’approccio geometrico appariva quasi sempre sintetico (anche se un’analisi geometrica appare in Newton), e quello algebrico sempre analitico. Così la procedura sintetica non era semplicemente l’inverso di quella analitica, ma la ricostruzione geometrica della soluzione simbolica talora era una procedura del tutto diversa. Nel complesso, più che l’antica opposizione analisi/sintesi trionfa l’idea di Viète di una generale intertraducibilità tra i diversi linguaggi matematici. L’alternativa fondamentale che segna la nascita della nuova scienza nel xvii e xviii secolo è quella tra metodi algoritmici simbolici e metodi geometrici.

La meccanica in origine era strutturalmente geometrica, nella sua tradizione archimedea (statica e quantitativa) come in quella aristotelica (dinamica e qualitativa), nelle sue radici ingegneristiche cinquecentesche come in Galileo e Newton. Anche se è sostanzialmente falsa la tesi di un Galileo insensibile alla misurazione numerica, è indubbio che tanto i suoi schemi argomentativi quanto la sua prassi sperimentale erano prevalentemente geometrici: è infatti l’osservazione astronomica il suo contributo sperimentale più rilevante. Anche Newton, nonostante le sue eccezionali capacità algebriche, scrisse i suoi Principia in uno stile quasi esclusivamente geometrico, senza formule. Tra i due anche Cartesio, padre del formalismo algebrico, scrive la sua Géométrie per tradurre i problemi geometrici in linguaggio algebrico, ma la sua fisica è tutta in una presentazione puramente geometrica, anche laddove una rappresentazione algebrica sembrava a portata di mano: nel moto dei gravi, nella teoria degli urti, nella legge di rifrazione.

Nel Seicento il linguaggio algebrico conserva il peccato originale di essere parte della tradizione pratica: uno strumento euristico, utile, ma inadatto a costruire una scienza. Una ars inveniendi, non una ars demonstrandi. Non è casuale allora che l’algebra diventi, soprattutto in Cartesio, parte essenziale del metodo: agli occhi del filosofo razionalista il metodo è tutto e quindi l’algebra è centrale, ma solo nel metodo e non come linguaggio di rappresentazione della realtà fisica; agli occhi del fisico empirista invece la scienza è tutto, ha carattere geometrico e quindi l’algebra è solo una tecnica spesso utile, ma fisicamente opaca.

La geometria analitica di Cartesio

La Géométrie di Cartesio è quanto di più diverso si possa immaginare dalla geometria di Euclide: non ci sono né assiomi né postulati, né definizioni né teoremi. Inizia semplicemente con la descrizione dell’isomorfismo tra operazioni aritmetiche e operazioni geometriche, tra cui il prodotto, poiché occorreva fare sì che il prodotto di due intervalli fosse un intervallo e non un rettangolo; la soluzione di Cartesio è proprio quella intuita da Bombelli (fig. 18). Bastano questi caratteri (nessuna struttura assiomatico-deduttiva, nessun principio di omogeneità) a confermare come l’algebra simbolica derivasse dalla tradizione pratica. Ma per Cartesio il metodo, e quindi l’algebra, ha un ruolo centrale, e così, diversamente da Viète, introduce una gerarchia: è la geometria che sempre più deve essere tradotta in linguaggio algebrico.

Fermat e Cartesio riescono ad associare equazioni a curve, distinguendo le curve geometriche da quelle meccaniche sulla base dell’esistenza di una singola equazione algebrica che la descrive (così per esempio la spirale non è geometrica poiché non la si può rappresentare senza coordinare un moto rettilineo con uno circolare). Così Cartesio classifica le curve dapprima sulla base di criteri geometrico-meccanici, quali la semplicità della macchina per tracciare la curva, ma alla fine si basa soprattutto sul grado dell’equazione.

La geometria proiettiva

Nella geometria nel Seicento francese non c’è solo l’analisi di Cartesio e Fermat. Un altro capitolo importante è la geometria proiettiva di Girard Desargues (1591-1661) e Blaise Pascal (1623-62). Essa appare legata soprattutto alla riscoperta della teoria delle sezioni coniche sviluppata nell’antichità, ma anche influenzata dalla prospettiva apparsa nell’arte e nell’ingegneria rinascimentale. In entrambi i casi la collocazione del centro di proiezione rispetto al piano di proiezione modifica la figura ottenuta dalla proiezione (un cerchio diventa un’ellisse, rette parallele diventano convergenti).

A Desargues si deve un teorema della geometria proiettiva che ha sempre attirato l’attenzione dei matematici: «Se due triangoli sono in prospettiva da un punto, allora i tre punti di intersezione dei lati corrispondenti sono allineati, e viceversa» (fig. 21). Il teorema è ovvio nello spazio, nel quale può essere dimostrato facilmente a partire dagli assiomi di incidenza. Nel piano invece la dimostrazione è stranamente più complessa e richiede l’assioma di congruenza fra i triangoli, a meno che non venga ottenuta come semplice proiezione del teorema dallo spazio sul piano.

Tangenti e quadrature

Sempre nella prima metà del xvii secolo si ripropongono due antichi problemi geometrici relativi a figure non rettilinee, diffusi soprattutto nel corpus archimedeo: la costruzione della tangente e la quadratura. Sono i problemi che saranno alla base della nascita del calcolo delle derivate e degli integrali. Perché questo accada nella matematica deve entrare in gioco il concetto di infinito, estraneo alla vita comune ma decisivo per la costruzione del mondo della fisica-matematica.

Tuttavia, in Fermat e Cartesio esistono tracce di un approccio finitista a quei problemi. L’idea di fondo è molto semplice: in problemi estremali, come la ricerca della tangente a una curva o la ricerca del massimo o minimo, accade che più soluzioni si identifichino. Per esempio Cartesio si pone il problema della costruzione algebrica della normale a una curva in un punto P (chiaramente equivalente alla costruzione della tangente). Considerando l’intersezione tra la curva e una circonferenza passante per P è chiaro che se il centro della circonferenza è sulla normale per P alla curva, allora P è una soluzione multipla (fig. 23).

Fermat si pone invece il problema del massimo di una funzione, per esempio bz ² − z ³ (viene qui usato anacronisticamente il termine «funzione», corrispondente a un concetto non ancora emerso: la formula in origine era infatti solo “qualche cosa di attaccato” a una curva per sintetizzarne aspetti di natura analitica). Fermat considera l’equazione bz ² − z ³ = c (fig. 22) e siano le radici x e y: egli osserva che per c troppo grande non ci sono soluzioni e che per c abbastanza piccolo ce ne sono due, ma che per il valore di c massimo della funzione le radici della equazione coincidono e quindi x = y. Da bx ² − by ² = x ³ − y ³, dividendo per x − y, consegue bx + by = x ² + xy + y ², e uguagliando le radici: 2b/3 = x, valore del massimo. Da notare che, sebbene sia facile tradurre queste procedure in termini di calcolo infinitesimale, esse sono in realtà procedure finite, e non occorre introdurre limiti o infinitesimi.

Questi concetti emergono invece da subito nell’altra questione: quella delle quadrature. L’idea è quella di calcolare un’area come una somma infinita di elementi, omogenei (una superficie somma di rettangoli sempre più stretti) o eterogenei (una superficie somma di segmenti). La seconda soluzione (gli indivisibili) appare per esempio nell’opera di Bonaventura Cavalieri (1598 ca-1647), la prima (gli infinitesimi) nell’opera di Giovanni Keplero (nome italianizzato di Johannes Kepler; 1571-1630) e di Pascal. Si fa strada la convinzione che i due approcci possano coincidere, ma l’idea intuitiva di un principio di continuità che porti un numero finito di rettangoli sempre più stretti a diventare infiniti intervalli ha un senso ancora troppo geometrico per fondare rigorosamente l’idea di limite.

John Wallis (1616-1703) tradurrà il linguaggio degli indivisibili in termini aritmetici e riterrà giustificato sfumare la distinzione tra infinitesimi e indivisibili finiti, considerando nella somma gli indivisibili di dimensione inferiore come infinitesimi omogenei. Il simbolo ∞ servirà tanto a contare il numero n di elementi da sommare, quanto a scrivere la loro dimensione 1/∞, la cui somma diventa finita quando n → ∞. L’idea di limite è in fondo estranea alla dottrina degli indivisibili, la quale è presente ancora in nuce in Leibniz, ma verrà poi presto abbandonata.

Il calcolo

Fra Cartesio e Newton la distanza è notevole. Cartesio segna il trionfo della filosofia meccanica, che si fonda su principi di carattere metafisico: il mondo descritto dal filosofo francese è fatto di corpi che si urtano, pendoli oscillanti, funi e pulegge, proiettili e gravi che cadono o restano in equilibrio. La sua geometria-meccanica concerne relazioni tra proprietà immanenti degli oggetti materiali (lunghezze, figure, tempi, pesi), come nella filosofia naturale medievale, con l’aggiunta della velocità, proprietà relativa, ma ormai quantificata come qualità intensiva già dai mertoniani e da Nicola di Oresme. L’algebra appare un linguaggio per esprimere problemi geometrici, e in qualche modo espressione di un metodo generale, ma non un linguaggio di rappresentazione della realtà fisica.

La fisica-matematica newtoniana si libera invece dello stile meccanico; essa tratta di enti non immanenti, come la forza di gravità, e di un mondo non più immanente nelle cose, ma a esse sottostante, i cui principi sono la matematica stessa e la prassi sperimentale. La meccanica è questo mondo di leggi, in cui forze e velocità sono oggetti realmente esistenti.

L’algebra comincia a diventare il calcolo, un linguaggio che abbandona completamente i termini della matematica antica (figure e numeri, fatti per parlare del mondo immediato dell’esperienza quotidiana) e tratta invece di enti matematici (differenziali, integrali, serie di potenze ecc.) del tutto estranei all’esperienza quotidiana, ma appartenenti al mondo artificiale in cui si fa scienza, il laboratorio. A tal fine occorre far fronte ai paradossi dell’infinito, a quel labirinto del continuo, che per Gottfried Wilhelm Leibniz (1646-1716), insieme al paradosso della giustizia divina, era la più grande sfida per il pensiero umano. E ciò non solo per sopravvivere a tale labirinto, ma per farne la base di una scienza del tutto nuova, capace di gestire il divenire di un regno tecnico, in cui l’empiria da naturale, qualitativa e semantica diviene artificiale, quantitativa e sintattica, da esperienza diviene esperimento.

La nuova meccanica fa riferimento a questo mondo tecnico, sottostante quello reale, di cui si vedono le tracce nelle figure geometriche. I mertoniani avevano rappresentato le configurazioni delle qualità intensive in schemi autonomi, senza connessioni con il mondo delle grandezze spaziali reali. In Galileo e in Christiaan Huygens (1629-95), invece, le figure esprimono nel contempo grandezze spaziali e velocità; in Newton appariranno anche le forze.

Le tematiche che sono alla base del futuro calcolo infinitesimale, come per esempio l’individuazione del centro di gravità dei solidi e i problemi di quadratura delle superfici curvilinee (aree delimitate da parabole, iperboli, spirali ecc.), si definiscono nel Cinquecento in seguito alla riscoperta dei testi archimedei. Anche la tecnica è quella archimedea del metodo di esaustione fondato sulla doppia riduzione all’assurdo, un metodo che a lungo venne considerato come il termine di riferimento rigoroso rispetto al quale gli strumenti simbolici presentavano solo il vantaggio della facilità d’uso; di qui la diffusa convinzione che i metodi analitici appena scoperti fossero sempre stati alla portata dei matematici greci. Mentre Wallis sottolineava come essi siano una ars inveniendi non confrontabile col rigore della ars demonstrandi, Leibniz attribuiva al calcolo simbolico un valore metafisico particolare. Solo nel Settecento l’approccio simbolico si affermerà definitivamente e bisognerà aspettare l’Ottocento perché la tecnica simbolica acquisti piena autonomia, indipendentemente dal presupposto geometrico.

Il primo tentativo di liberarsi della tradizione sintetica antica appare probabilmente in Stevin, che cerca di porre il problema in termini logici: supposto che «se due quantità differiscono, esse differiscono per una quantità non nulla», allora «due quantità che differiscono per meno di ogni quantità non nulla non sono differenti».

Vi è qui il nucleo dell’idea di limite e di infinitesimo. Ma perché l’approccio simbolico non era stato sviluppato dai greci in luogo del complesso metodo di esaustione? I greci, oltre a scontare le difficoltà legate all’idea di infinito, non potevano concepire concetti negativi come lo zero (il numero era sempre finito e determinato, un semplice aggettivo), né abbinare concetti geometrici (grandezza) con concetti aritmetici (differenza). Invece alla fine del medioevo lo zero era ormai accettato e svaniva l’opposizione tra geometria e aritmetica (come nell’assioma aritmetico-geometrico medievale «il tutto è uguale alla somma delle parti»).

Certo in Stevin o in Galileo lo zero come numero reale non appare se non come una sorta di limite delle grandezze verso il “nulla”, ma l’idea di una grandezza minore di qualsiasi grandezza (un infinitesimo) non era assurda: poteva essere una semplice superficie, come nella celebre scodella di Galileo, in cui «la circonferenza di un cerchio immenso possa chiamarsi eguale a un sol punto»: in fig. 24 il semicerchio AFB ruotando intorno all’asse FC descrive una semisfera, il triangolo CDE descrive un cono, il rettangolo ABED un cilindro. Per ogni punto P sull’asse si verifica con semplici calcoli che l’area del settore circolare formato nella rotazione da ON è uguale all’area del cerchio di raggio PL. Questa relazione vale per ogni L, e in particolare per C, laddove il settore circolare diviene una circonferenza e il cerchio diventa un punto.

Idee analoghe si ritrovano per esempio in Luca Valerio (1552 ca-1618), che osserva come la differenza tra cilindri circoscritti e inscritti a un paraboloide (fig. 25) sia uguale all’ultimo cilindro circoscritto (risultato già noto ad Archimede), e come, aumentando il numero di cilindri, essa possa essere resa minore di qualsivoglia volume e di conseguenza si possa trovare il centro di gravità considerando una sola delle due sequenze di cilindri. Ma il suo approccio è solo geometrico e l’idea di limite appare remota.

In relazione allo stesso problema Stevin scoprirà che le approssimazioni attraverso i cilindri pongono il centro di massa a un terzo dell’altezza più una quantità che si dimezza al raddoppiare del numero di cilindri, e può quindi essere resa minore di qualsiasi quantità, ma tradurrà infine il ragionamento in una argomentazione analoga al metodo di esaustione.

Un’altra fonte di ispirazione del calcolo infinitesimale veniva dalle somme di sequenze di numeri. Per esempio molti matematici, tra cui Wallis, si resero conto che le somme delle potenze degli interi

mostravano una certa regolarità.

Si sapeva che

e che

(dove ≅ denota un’approssimazione sempre migliore al crescere di n), e per qualunque k la somma sembrava approssimare il valore n^k+1/(k + 1).Wallis arrivò a estendere tale risultato anche per k fratto. In realtà questi risultati non erano dimostrati, ma verificati fino a certi valori finiti di n e di k, ed estesi per “analogia”. Da essi poi Wallis con una idea intuitiva di “interpolazione” ricavava una formula per il calcolo di π:

L’interesse per le somme finite si saldava così con l’interesse per le somme infinite, le serie (il cui calcolo era pure tutt’altro che rigoroso), usate anche per calcolare le aree sottese a certe curve. È molto nota la quadratura della iperbole proposta da Gerardo Mercatore (nome italianizzato di Gerhard Kremer; 1512-1594). Data l’iperbole di equazione y = 1/(1 + x), l’area tratteggiata (fig. 26) veniva approssimata come somma di rettangoli circoscritti le cui aree erano poi sviluppate come serie geometriche, e, usando le approssimazioni di Wallis sopra citate, risultava essere uguale a T − T ²/2 + T ³/3 − T ⁴/4 + ... = log(1 + T ).

Per gli sviluppi in serie merita di essere ricordata una tecnica che sarà portata al massimo sviluppo da Newton grazie all’uso formale degli algoritmi aritmetici. Per esempio, per sviluppare in serie la funzione ƒ(x) = 1/(1 + x) basta dividere 1 per (1 + x) applicando le usuali regole della divisione in colonna, così da ottenere 1 − x + x² − x ³ + ... Analogamente, lo sviluppo in serie di una formula sotto il radicale si ottiene sviluppando l’algoritmo in colonna per l’estrazione della radice.

Questa tecnica fa toccare con mano non solo l’origine pratica del calcolo infinitesimale, ma soprattutto la sua natura algoritmica fondata sulla fiducia nel trattamento simbolico corroborata dal suo successo. Molti filosofi criticarono l’approccio simbolico, soprattutto in Inghilterra: Hobbes lo definiva «una scabbia di simboli», Berkeley chiamava gli infinitesimi «fantasmi di quantità defunte». Una qualche diffidenza era diffusa anche tra i matematici. Del resto, nella usuale definizione di derivata si divideva per un infinitesimo il quale poi nel calcolo veniva posto uguale a zero, il che dal punto di vista aritmetico è un errore. Certo, si intuiva che la procedura aveva una natura algoritmica e non dimostrativa, ma il problema dello status del calcolo infinitesimale simbolico resterà di fatto aperto fino all’Ottocento, fino a quando cioè Weierstrass fornì una definizione logicamente rigorosa del limite di una funzione.

Una terza via al calcolo infinitesimale era l’approccio cinematico, nel quale la curva è la traiettoria descritta da un corpo/punto in movimento. In questo approccio la tangente era la traiettoria del moto che il corpo avrebbe percorso per inerzia. La stessa teoria cartesiana delle curve faceva spesso riferimento al tracciamento della curva tramite moti complessi. Anche funzioni come il seno e il logaritmo erano state definite come sovrapposizione o confronto di due moti. L’importanza della lettura cinematica della derivata non stava solo nelle applicazioni fisiche del calcolo, ma anche nel fatto che la connessione meccanico-geometrica ne fornì il vero senso per circa due secoli: di fronte alle incertezze e contraddizioni del calcolo si potevano sempre ricondurre derivate e integrali tanto al moto e allo spazio percorso quanto alla tangente e all’area.

Newton e Leibniz

Nella seconda metà del secolo xvii il calcolo infinitesimale assume nell’opera di Newton e Leibniz la forma che, almeno dal punto di vista delle tecniche, ha conservato fino a oggi. Nonostante le feroci polemiche tra i due sulla priorità della scoperta, i loro approcci erano equivalenti (almeno per quanto riguarda gli aspetti algoritmici), ma le differenze concettuali erano nette ed evidenziano il complesso processo cognitivo che ha portato all’elaborazione del calcolo infinitesimale.

Il problema di partenza era il trattamento del continuo come tema sia matematico (area e tangenti delle figure curve), sia meccanico (il moto). Le radici del “labirinto del continuo” consistevano nel fatto che si potesse parlare di un istante o punto “successivo”, ma non dell’istante o del punto “immediatamente successivo” oppure che si potesse ottenere una grandezza finita dalla somma di valori nulli. Era il cuore degli insuperabili paradossi che si incontravano quando si pensava il continuo come composto di indivisibili di misura nulla, punti per segmenti, segmenti per superfici, superfici per solidi.

Newton e Leibniz affrontano il problema da due punti di partenza distinti, anche se entrambi centrati sulla difficoltà di trattare pure gli infinitesimi, cioè grandezze infinitamente piccole ma non nulle, e orientati a cercare un’idea intuitiva di limite (per Newton) o un’idea metafisica di continuità (per Leibniz). La soluzione per distinguere gli infinitesimi dagli indivisibili fu trovata sostituendo il punto “immediatamente successivo” a un punto P con un punto P ′ ≠ P che però si può avvicinare quanto si vuole a P, considerando quindi un intervallo PP ′ non nullo ma nel contempo minore di ogni intervallo finito.

Newton lo fa concependo una curva descritta da un moto locale, e quindi in termini spaziali, usando il tempo come variabile indipendente. Considera sempre una grandezza fisica fluente x, il cui mutamento chiama flussione, indicato con ẋ, considerato un attributo della variabile x. È una “geometria del moto” in cui si può riconoscere una tradizione tipicamente inglese, dai mertoniani ai logaritmi di Nepero (nome italianizzato di John Napier, 1550-1617) e alla matematica di Isaac Barrow (1630-77), il maestro di Newton, che sviluppa una concezione cinematica di processi continui. Newton considera un tempo infinitesimo, denotato in genere con o, così che un aumento infinitesimo (momento) di x risulta o ⋅ ẋ: il momento della linea è inteso come «un segmento infinitamente breve», ma non nullo. Le difficolta vengono aggirate dall’idea cinematica, sostenendo il carattere potenziale e non attuale dell’infinito processo al limite.

Occorre notare che tale tecnica viene applicata uniformemente a tutta l’equazione, differenziando cioè tutti i termini contenenti fluenti (per esempio x e y) per ottenere un’equazione contenente fluenti e flussioni. Per trovare la tangente occorrerà risolverla ottenendo il rapporto ẏ / ẋ.

Da un punto di vista algoritmico il calcolo si basa sulla flussione della potenza xⁿ. Questo risultato viene ottenuto da z = xⁿ scrivendo z + ż ⋅ o = (x + ẋ ⋅ o)ⁿ, sviluppando il secondo membro, sottraendo z = xⁿ, dividendo per o, trascurando tutti i termini contenenti o, e ottenendo ż = n x^{n − 1} ẋ . Per funzioni più complesse strumento chiave è la teoria delle serie, tramite la quale tali funzioni vengono ridotte a somme di potenze, che per Newton sono anche uno strumento di calcolo approssimato. All’interno di questa tecnica si inserisce anche l’estensione dello sviluppo della potenza del binomio a potenze anche frazionarie e negative: se la potenza è un intero positivo lo sviluppo dà un polinomio, altrimenti si ottiene una serie di potenze. Questa tecnica appare sicuramente più fondata della semplice interpolazione e analogia di Wallis, anche se in definitiva è basata su una presupposta omogeneità algoritmica tra finito e infinito.

Col tempo Newton si distaccherà, almeno dal punto di vista teorico e nella sua fisica, dall’approccio algebrico-simbolico (il punto di svolta si può collocare negli anni Settanta, ma all’inizio del Settecento Newton sembra riconsiderare questa scelta) a vantaggio di un approccio geometrico e fondato sui rapporti, secondo l’antica tradizione teorica, così che gli infinitesimi saranno per lui solo una notazione conveniente da sostituire nei calcoli rigorosi con il “metodo dei primi e ultimi rapporti” (limite di rapporti incrementali). In termini geometrici, l’idea rigorosa è che quando due punti sulla curva tendono a coincidere anche i rapporti tra arco, tangente e secante sulla curva tendono all’uguaglianza. Newton insisterà che non si tratta di studiare un rapporto tra infinitesimi, ma di studiare un rapporto tra quantità finite che, in quanto ben definito, “tende” a un limite ben definito, e considererà il suo calcolo coincidente con quello degli antichi liberato dei “fastidi” della dimostrazione per assurdo del metodo di esaustione. Per difendersi dalle critiche sulla inesistenza del rapporto tra quantità evanescenti Newton farà il paragone con un corpo in moto che all’improvviso si arresta, considerando la sua “ultima” velocità al momento dello stop: anche essa prima dello stop non è l’ultima e allo stop non c’è più. Un ragionamento che richiama le disquisizioni scolastiche su incipit e desinit, l’inizio e la fine degli eventi. In trasparenza emerge un atteggiamento già riscontrabile in Galileo: la difficoltà a considerare lo zero un numero reale, l’elemento di separazione di numeri positivi e negativi, piuttosto che solo il semplice svanire di una grandezza.

La fig. 27 mostra il ragionamento che porta Newton al teorema fondamentale del calcolo, al fatto cioè che derivazione e integrazione sono due operazioni che di fatto possono considerarsi inverse l’una dell’altra, e mostra anche come il linguaggio delle proporzioni resti alla base del ragionamento geometrico. Newton pone AC = 1, z e x sono le aree rispettivamente al di sotto della curva e al di sotto dell’asse (e quindi x è anche l’ascissa). Di conseguenza le flussioni di z e x sono rispettivamente DB e BE = 1. DB sarà quindi anche il rapporto tra le flussioni di z e di x, che potremmo chiamare la derivata di z rispetto a x. Ma z è l’integrale della curva, la quale curva quindi coincide con la derivata del suo integrale.

Per Newton la cinematica era il fondamento del calcolo, il suo metodo derivava direttamente dalla natura, e questo era il motivo per la preferenza nei confronti dell’approccio geometrico e la diffidenza verso quello simbolico; il calcolo era qualcosa di “evidente” per enti geometrici, poco credibile per semplici simboli; le entità geometriche “esistevano”, mentre il trattamento simbolico introduceva enti immaginari e infinitesimi. Quando era tradotta in linguaggio naturale, la geometria funzionava, l’algebra invece “provocava nausea”, era ridondante, aveva un ruolo solo euristico e un carattere meccanico privo di chiarezza referenziale; le dimostrazioni geometriche avevano invece un chiaro contenuto, e tutto un complesso processo aritmetico corrispondeva al semplice tracciamento di una linea. Quindi il metodo sintetico delle flussioni, basato sul moto continuo e sui “primi e ultimi rapporti”, anziché su infinitesimi, era preferibile a quello analitico.

L’approccio di Leibniz era diverso e si basava sulle somme e differenze finite, generalizzate per diventare infinitesime. In una lettera a Wallis così scrive: «[...] mi accorsi che le differenze corrispondevano alle tangenti e le somme alle quadrature [...]». Il linguaggio della teoria delle proporzioni, centrale in tutta la storia della matematica fino ai suoi tempi, gli sembra inutile.

L’idea del triangolo caratteristico, formato con i cateti Δx e Δy, era già apparsa in Pascal ed è la base della connessione tra la teoria degli infinitesimi e lo studio delle tangenti. Leibniz dirà di essere rimasto stupito di come Pascal non ne avesse colto le potenzialità, ma occorre ricordare come ciò richiedesse da un lato una fusione tra geometria e aritmetica (la determinazione della tangente, fatto tipicamente geometrico e quasi iconico, riconducibile a differenze versus il concetto aritmetico di differenze e rapporti tra ordinate e ascisse) all’epoca ancora in statu nascendi, dall’altro un trattamento algoritmico degli infinitesimi.

Nella fig. 28 il triangolo caratteristico è TPM, simile al triangolo PAS (e anche al triangolo PAN, con PN normale alla curva). Poiché T e P′ si confondono, in quanto A e A′ sono infinitamente vicini, si ottiene che il rapporto tra gli infinitesimi P′M e PM è uguale al rapporto tra l’ordinata AP e la subtangente SA. Pascal aveva usato tale rapporto per studiare i problemi di quadratura, Barrow per studiare quelli relativi alle tangenti. Risulta tuttavia evidente dalla figura che, come la quadratura è la somma dei valori della funzione in rettangolini infinitesimi, così la tangente è individuata dalla differenza tra i valori della funzione in punti la cui distanza è infinitesima. L’addizione è però l’operazione inversa della differenza, e risulta anche chiaro che la differenza tra le due quadrature di ƒ(x) nei punti x + dx e x è proprio la ƒ(x) moltiplicata per dx: dividendo per dx si ottiene così il teorema fondamentale del calcolo.

Quella di Leibniz è una “aritmetica dell’infinito” e il suo approccio è esplicitamente simbolico e algoritmico, nei suoi fondamenti e non solo in pratica (come voleva Newton): in una lettera a Henry Oldenburg egli così scrive: «Tutto il calcolo differenziale appare solo un aspetto di una arte combinatoria generale, un alfabeto del pensiero umano», connaturata all’arte umana della scoperta, l’ars inveniendi, quasi un metalinguaggio rispetto al linguaggio aritmetico o algebrico.

Anche per Leibniz gli infinitesimi non esistono realmente, tuttavia l’infinitamente piccolo non gli appare un artificio, un inganno che ostacola lo sviluppo delle leggi naturali, ma qualcosa che ha un fondamento reale legato al ruolo dell’infinito, che entra nella realtà non materialmente, ma come fondamento intellettuale nel principio di continuità. Il differenziale è un ente simbolico, non è un infinitesimo, anche se è incomparabilmente minore delle quantità ordinarie, talora inteso come una variabile, talora come una costante, e comunque sempre omogeneo alla grandezza differenziata. Per Leibniz, dato un numero dx, dy è quel numero tale che dy /dx è la pendenza della tangente: il differenziale appare quindi un numero non nullo, «una linea retta scelta arbitrariamente» e la tangente «la linea che connette due punti a distanza infinitamente piccola» o «il lato di un poligono con un infinito numero di angoli». Il ruolo svolto in Newton dall’idea di limite viene svolto in Leibniz dal principio di continuità: «in ogni transizione supposta terminante in qualsiasi termine, si può istituire un ragionamento generale in cui tale termine finale è incluso». I differenziali violavano sì il principio di Archimede, erano diversi da 0 ma in fondo erano indistinguibili da esso, tuttavia per il principio di continuità potevano essere trattati come quantità ordinarie: non erano enti reali bensì “finzioni ben fondate” (come il continuo stesso), e servivano tramite la loro algebra a fare i calcoli.

Inizialmente Leibniz non usa l’idea di limite e scrive

come una totalità, una sorta di “somma di linee”, come nelle dottrine degli indivisibili di Cavalieri e Wallis; solo successivamente scriverà

come una somma di rettangoli infinitesimi, quando si rafforza la preclusione verso gli indivisibili.

Anch’egli stabilisce senza prova le regole della differenziazione, usando implicitamente l’idea di infinitesimi, i differenziali di variabili come differenze variabili, e così la d agisce come un operatore, in modo da permettere di definire differenziali di ordine superiore, qualcosa di difficile nell’approccio geometrico newtoniano. E la differenziazione, per Leibniz, non si applica genericamente a una equazione (come in Newton) bensì a una funzione (usa proprio questo termine per indicare quantità geometriche, coordinate, tangente, corda ecc. associate a una curva): una grandezza geometrica legata alle altre tramite un’espressione algebrica.

Il regno dei segni

Il xvii secolo è coronato dalla pubblicazione dei Principia newtoniani, nei quali la nuova fisica viene costruita non con il linguaggio del calcolo simbolico ma con i concetti della geometria. Tuttavia l’algebra simbolica si era ritagliata uno spazio crescente, anche se all’inizio era adoperata solo perché i segni aiutavano la memoria, esplicitavano i passaggi, semplificavano gli algoritmi, e quindi essa apparteneva alla tradizione pratica come forma paradigmatica dell’ars inveniendi. Ma si diffondeva l’impressione che essa aprisse nuove strade precluse al ragionamento geometrico, segnando così il tramonto del metodo di esaustione. E non è forse casuale che grandi analisti come Viète e Wallis si impegnassero anche come decrittatori di codici.

In questa diffusione del simbolismo algebrico si affacciava un processo che dominerà la matematica moderna e in realtà la stessa civiltà moderna: l’“irresistibile ascesa” del regno dei segni.

I segni, come già nella matematica islamica, non erano più usati solo per registrare i valori numerici, ma diventavano gli ingredienti essenziali della scrittura degli algoritmi: da un lato oggetti concreti, scrivibili, leggibili, manipolabili, spostabili, e quindi trattabili algoritmicamente, dall’altro enti ideali, gli unici per i quali si potesse predicare una “assoluta uguaglianza” o una “assoluta differenza”: due segni come 7 rappresentano lo stesso numero anche se sono scritti con grafia diversa, mentre 4 e 5 sono numeri del tutto diversi anche se talora scritti in modo simile.

L’ars combinatoria

Della nuova matematica che si andava profilando con la centralità del registro simbolico il testimone più autorevole fu Leibniz. In ciò consisteva anche la differenza essenziale rispetto a Newton, per il quale il simbolismo aveva un ruolo secondario. La notazione simbolica è per Leibniz «un mezzo sensibile e palpabile che guida la mente»: si pensi per esempio alla forma autoesplicativa che assume nella notazione di Leibniz la regola di derivazione della funzione composta: dz /dx = dz /dy × dy /dx. Il suo linguaggio algebrico si adatterà al trattamento del continuo creando una sintassi in grado di evitare i paradossi noti già ai greci. Considerare il punto y + dy significa in fondo solo prendere il punto che “viene dopo” y, così che dy è diverso da zero perché il punto è distinto, ma poi si pone uguale a zero perché la distanza tra i due punti deve essere minore di ogni possibile distanza finita, altrimenti vi sarebbero altri punti intermedi, e questo nel “continuo aritmetico” significherebbe zero: in una lettera a Oldenburg è scritto che dy è «la differenza delle due y più vicine».

L’ars combinatoria di Leibniz si delinea sin dall’inizio come la scienza della pratica simbolica che la rende nel contempo prassi algoritmica e linguaggio della scienza umana. La sua idea giovanile e cartesiana di un “alfabeto del pensiero umano” evolve nell’idea che in realtà l’uomo conosca solo attraverso i segni, un’idea che influenzerà sia l’algebra sia l’analisi combinatoria sia la logica formale, quasi una profezia dei futuri linguaggi algoritmici.

Un tema ricorrente nell’opera di Leibniz è l’idea di una doppia funzionalità del trattamento sintattico, come characteristica universalis, cioè come capacità del linguaggio simbolico di rappresentare compiutamente l’universo oggetto di una scienza, e come calculus ratiocinator, cioè come capacità algoritmica di effettuare ragionamenti inoppugnabili manipolando segni. Di qui l’utopia razionalista di Leibniz, secondo cui un giorno ogni diatriba filosofica sarebbe stata risolta semplicemente calcolando: c’è addirittura in Leibniz la convinzione che ogni verità (anche quando ci appare “empirica”) sia, per un essere capace di deduzioni anche infinite, sempre analitica, riducibile cioè all’inclusione del predicato nel soggetto.

Sulla via dei segni si dovrà incamminare anche la logica. Sarà Leibniz il primo ad asserire la natura analitica delle verità matematiche, il loro essere deducibili come verità logiche, puramente formali, a prescindere dal loro contenuto. Nei lavori analitici di Leibniz già si intravede la futura logica matematica, in cui dimostrazione e calcolo coincidono, giacché condividono la stessa natura algoritmica.

È una logica che non può essere confrontata né con quella medievale, che era una logica dei termini del linguaggio naturale, né con quella antica, che era un’immagine esplicativa della phýsis. Nella logica leibniziana appare inoltre un’idea, che avrà un ruolo centrale nella logica moderna: quella della possibile “aritmetizzazione” del pensiero, nel senso della sua riduzione al calcolo, nel quale cioè le idee complesse possano essere ottenute da operazioni aritmetiche (moltiplicazioni o addizioni) sui numeri associati alle idee semplici. Il pensiero di Leibniz appare lo sviluppo più coerente dell’idea, già intravista nel Cinquecento, che all’interno dell’argomentazione matematica ci fosse il nucleo di una logica generale della scienza di cui il sillogismo era solo un capitolo, un’idea spesso contrassegnata come mathesis universalis, che svolgeva un ruolo centrale nel metodo di Cartesio.

Nel Seicento appare, non solo in Leibniz, l’idea che l’uomo possa conoscere il mondo con la stessa certezza con cui lo conosce Dio, unica differenza essendo la finitezza dell’uomo di fronte all’infinitezza divina; ciò farà dell’infinito l’orizzonte della nuova scienza: i numeri reali, le serie, i limiti saranno i concetti infinitari che caratterizzeranno la matematica nei secoli successivi. E anche essi si riveleranno problematici per la matematica tradizionale geometrica, richiedendo invece una matematica sintattica e logica, svincolata da intuizioni geometriche o attrazioni fisico-meccaniche, legate al movimento.

Oltre che alla matematica, la logica del Seicento si legava anche alle scienze naturali. Per esempio, nella logica di Port Royal, si trova la distinzione, impalpabile in Aristotele e vagamente accennata nei logici medievali, tra intensione ed estensione di un predicato: per esempio, dell’aggettivo «rosso» l’estensione era l’insieme degli oggetti rossi, l’intensione era invece il concetto di «rosso», cioè un ente essenzialmente mentale. Era una distinzione chiara anche a Leibniz, ma per lui probabilmente irrilevante poiché i due ambiti erano legati in una armonia prestabilita. Nel secolo successivo Eulero introdurrà quella rappresentazione insiemistica estensionale (i diagrammi di Eulero-Venn) che ancora oggi si insegna nelle nostre scuole (fig. 29).

Più in generale si diffondeva l’idea che quel mondo reale ma inattingibile alla conoscenza comune, che era divenuto l’oggetto della scienza, avesse una struttura simbolica. Era conoscibile solo in laboratorio ma, come osserverà il matematico tedesco Hermann Weyl (1885-1955), anche la misura sperimentale è in fondo solo il confronto tra due segni, uno risultato dalla manipolazione di leggi naturali in forma algebrica e uno letto su uno strumento di misura. Nel giro di un secolo tutta la fisica sarà scritta in linguaggio algebrico, tramite funzioni ed equazioni.

Il Settecento

All’inizio del nuovo secolo, per difendere le tecniche simboliche, di sicura efficacia ma di dubbio fondamento, d’Alembert esortava: «Le calcul porte sa preuve avec soi»; e ancora «Allez de l’avant, la foi viendra ensuite».

Il Settecento è caratterizzato dall’opera di grandi fisici-matematici, quali i Bernoulli (Jakob, 1654-1705; Johann, 1667-1748; Daniel, 1700-82), Eulero (nome italianizzato di Leonhard Euler, 1707-83), Jean-Baptiste Le Rond d’Alembert (1717-83), Joseph-Louis Lagrange (1736-1813), che hanno dato al calcolo infinitesimale la sua forma analitica attuale. A prima vista potrebbe sembrare una fase “minore”, ma ci sono due aspetti di questa “sistemazione” che vanno sottolineati: la netta separazione tra filosofia e scienza fisica-matematica, e il passaggio, progressivo ma definitivo, del calcolo infinitesimale dalla forma geometrica a quella algebrica. Questo aspetto sintattico fa da sfondo alla poderosa tecnica per l’applicazione della analisi alla fisica-matematica: la risoluzione delle equazioni differenziali.

Il primo testo sul calcolo è quello di Guillaume-François-Antoine de l’Hôpital, Analyse des infiniment petits pour l’intelligence des lignes courbes, pubblicato nel 1696, ma dovuto in gran parte a Johann Bernoulli. In esso appaiono le definizioni di “quantità variabile”, che cresce o decresce con continuità e la cui parte infinitamente piccola è il differenziale, e due postulati: uno più aritmetico («Due quantità la cui differenza è una quantità infinitamente piccola possono essere prese o usate indifferentemente»), e uno di carattere più geometrico («Una curva può essere considerata come un poligono con un infinito numero di lati, ognuno di lunghezza infinitamente piccola, che determinano la curvatura della curva dagli angoli che fanno tra di loro»).

Si esplicita il concetto di funzione come espressione: per Eulero essa è «una espressione analitica comunque composta della quantità variabile e di numeri o quantità costanti»; per Lagrange è «un’espressione algebrica comunque composta di variabili e contenente un numero qualsiasi di costanti». La stessa derivata diventa allora una funzione. Il carattere “sostanziale” delle espressioni algebriche (anche infinite) appare nel fatto che per Lagrange la serie di potenze diventa la forma più generale per esprimere una funzione, e la continuità viene caratterizzata dall’esistenza di un’unica espressione algebrica per la funzione. Parallelamente, inizia il processo di traduzione della meccanica newtoniana nel formalismo di Leibniz.

I matematici del Settecento accettano inizialmente l’esistenza degli infinitesimi più dei “padri fondatori” Newton e Leibniz: per Johann Bernoulli «nella misura in cui il numero dei termini è infinito, l’infinitesimo esiste ipso facto». Ma in realtà l’approccio realista e pragmatico al calcolo (sia nella sua versione geometrica sia in quella simbolica) stava tramontando a vantaggio di un metodo puramente algoritmico, senza riferimento agli infinitesimi (usati solo per tradurre il problema in una equazione differenziale) alle figure geometriche o al moto. Così il problema “metafisico” della loro natura riceveva soluzioni che oggi possono apparire bizzarre: per Eulero il differenziale non è altro che lo zero e il calcolo è solo una procedura per espressioni del tipo 0/0 che per scopi pratici utilizza i differenziali, e motiva la sua opinione facendo vedere come la loro manipolazione si possa ricondurre a proprietà dello zero; lo storico della matematica Carl B. Boyer scrive che di 28 pubblicazioni tra il 1754 e il 1784 da lui analizzate, 15 interpretano il calcolo con i differenziali leibniziani, 6 in termini di limiti, 4 in termini di zero euleriano; Lagrange invece definiva le derivate come i coefficienti nello sviluppo in serie di Taylor:

In Eulero il calcolo infinitesimale ha ancora caratteri spiccatamente geometrici, ma nel 1788 Lagrange pubblica la sua Mécanique analytique, la più importante opera scientifica dopo i Principia newtoniani, nella quale si vanta di non utilizzare più figure ma solo formule (e lo fa veramente: un libro di 600 pagine senza neanche una figura). Con l’affermarsi della forma algebrica simbolica, la nuova analisi infinitesimale diventava sempre più la base non solo della meccanica ma della fisica tout court (astronomia, acustica, ottica, teoria del calore).

Anche la teoria delle equazioni differenziali parziali, legata al concetto di funzione, cresceva intorno a problemi di fisica. Uno dei più celebri fu quello delle corde vibranti, la cui forma è data da una funzione u(x, t) soluzione dell’equazione differenziale

Nel caso di un’onda stazionaria (le oscillazioni delle corde degli strumenti musicali non si propagano nello spazio) la soluzione dell’equazione è una somma di sinusoidi, e quindi periodica. La discussione tra d’Alembert ed Eulero in questo studio riguardava la funzione iniziale, se dovesse essere già periodica, come voleva d’Alembert, oppure no, come voleva Eulero, sulla base della plausibilità fisica: infatti una corda ferma viene di solito messa in vibrazione tirandola per il suo punto medio e poi lasciandola andare: ha quindi una forma iniziale non periodica (è una spezzata formata da due segmenti di retta, fig. 30).

Caratteristica dell’epoca è la quasi impossibilità di distinguere tra matematica e fisica, come per esempio nel calcolo delle variazioni. Esso appare con il problema della brachistòcrona: la curva che, dati due punti a diversa altezza, in presenza della sola gravità e del vincolo di seguire la curva, consente la discesa tra essi in un tempo minimo (non è la retta, che dà invece la curva di minima lunghezza, fig. 31).

Si tratta di un problema di minimo in una famiglia di curve, affrontato alla fine del xvii secolo da Johann e Jakob Bernoulli. Essi studiarono in generale il problema di trovare in una famiglia di curve (funzioni) F quella che minimizzava il valore di una certa funzione (il tempo, nel caso della brachistòcrona) che dipendeva dalla curva variabile in F, una funzione di funzione che assumerà il nome di funzionale. A questo fine Lagrange distinguerà tra d che esprime la differenziazione lungo la curva, e δ, che esprime la variazione in una famiglia di curve. Tali problemi di minimizzazione apparivano sempre più spesso in una meccanica che andava assumendo una forma diversa da quella newtoniana, giacché si fondava su diversi principi, quali il principio di minima azione, il principio dei lavori virtuali, il principio della minima altezza del centro di massa, i principi di conservazione. Il calcolo delle variazioni è alla radice della moderna analisi funzionale, ma la sua motivazione originaria era fisica e problemi fisici ne segnarono lo sviluppo. Essenzialmente fisico fu l’esito principale di tale teoria: la meccanica lagrangiana, che diventerà lo standard della fisica dalla fine del xviii secolo.

Non diversa fu l’evoluzione di un altro capitolo della matematica settecentesca: il metodo dei moltiplicatori di Lagrange, sviluppato per studiare il minimo o massimo di una funzione tra punti vincolati a variare su una linea o una superficie. Detta ƒ la funzione e detti g_i = 0 i vincoli, il metodo consisteva nel minimizzare la funzione ƒ + l₁g₁ + l₂g₂ +...+ l_ng_n al variare non solo delle incognite ma anche dei parametri l_i. Il metodo ha una elegante motivazione matematica (in fondo riconducibile alla intuizione di Cartesio e Fermat che un punto di massimo o minimo è anche un punto multiplo, in cui cioè più soluzioni vengono a coincidere), ma ammetteva anche una parallela motivazione fisica: le linee o superfici di vincolo per il moto di un corpo potevano essere determinate dall’azione di forze (quali per esempio una pressione o una resistenza che costringevano il corpo a muoversi sulla linea o superficie), e allora il moto veniva dedotto dai principi di minimo della meccanica applicati senza i vincoli ma in cui fossero presenti anche tali forze, il cui valore era proprio dato dagli l_i. Quanto nell’opera di Lagrange derivasse dal problema matematico e quanto derivasse dal problema fisico è difficile da dire; in realtà l’impressione è che mai come nel Settecento tra meccanica e calcolo simbolico la distinzione sia stata impalpabile.

Nel 1744 Pierre-Louis Moreau de Maupertuis (1698-1759) introduceva il principio di minima azione: prendeva le mosse dal problema della rifrazione di un raggio di luce, ma in realtà rispondeva a sollecitazioni teologiche. Eulero dava a tale principio un fondamento più fisico, ma dal 1768 al 1772 nelle sue Lettere a una principessa tedesca sulla filosofia naturale tornava a fondere a sua volta fisica, matematica, filosofia e teologia quasi senza soluzione di continuità. Ma quando nel 1779 l’Accademia delle scienze di Berlino indisse un concorso sul tema delle “cause” della forza, tema classico nel dibattito sulla fisica newtoniana, vi parteciparono molti filosofi, ma nessun fisico-matematico. Nella Mécanique analytique di Lagrange del 1788 gli aspetti filosofici sono ormai del tutto assenti. Ormai la fisica-matematica si era definitivamente separata dalla filosofia: il suo fondamento risiedeva esclusivamente nella capacità di risolvere i problemi fisici.

Questa frattura era una delle facce della cultura illuminista e della rivoluzione industriale che si stava diffondendo a partire dall’Inghilterra. Con la rivoluzione francese si afferma il sistema metrico decimale, con il metro campione. I sistemi metrici tradizionali (come quello ancora oggi diffuso in Inghilterra e usa) erano basati sull’esistenza di unità eterogenee (piedi, cubiti, pollici ecc.) legate da rapporti convenzionali. Era un’idea puramente aritmetica applicata al continuo e che rimaneva estranea al numero reale. Il nuovo sistema rifletteva invece l’emergere del continuo numerico e cioè di una struttura numerica infinitamente e omogeneamente divisibile, che nell’Ottocento si estenderà a tutte le misure fisiche.

La matematica moderna

La separazione tra fisica-matematica e filosofia è una svolta epocale: al collegamento esplicito tra scienza e filosofia si sostituisce una sorta di “contiguità e competizione cognitiva” tra esse. È soprattutto in Immanuel Kant (1724-1804) che questo passaggio appare inizialmente: la sua “metafisica” differisce nettamente dalla metafisica tradizionale e si caratterizza piuttosto come una indagine critica sulle condizioni a priori della scienza, che ne garantisca tanto la struttura razionale quanto il carattere empirico. Con Kant svanisce l’idea, indiscussa sino dalla antichità, che fonti della conoscenza siano solo l’esperienza e la deduzione (con assiomi garantiti dall’evidenza); al centro dell’attività scientifica si colloca il soggetto della conoscenza, un po’ immagine della città scientifica, che non contempla la natura ma le “impone” di rispondere alle domande che egli formula e le fornisce anche la cornice generale in cui la stessa empiria deve essere inserita.

Sulla scia di Kant l’Ottocento vede la nascita di autentiche “filosofie della scienza”, di stampo più idealista in Germania, più empirista in Inghilterra. Il preminente ruolo della filosofia nelle università tedesche arricchisce anche la matematica di sfumature filosofiche, ma l’organica connessione tra filosofia naturale e fisica-matematica è perduta per sempre. La fine dell’Ottocento vedrà anzi nel mondo matematico delinearsi un’autonoma capacità di farsi filosofia. Non casualmente i due testi più influenti della nuova geometria, la Habilitationschrift di Riemann del 1854 e l’Erlanger Programm di Klein del 1872, saranno letti da due geometri “puri” davanti a un pubblico di filosofi.

Semantica e sintassi

La separazione tra scienza e filosofia si affiancava alla nuova collocazione dell’algebra simbolica, da un lato ormai perfetto linguaggio della fisica-matematica, dall’altro però ancora costretta a trovare il suo senso nella geometria (la derivata e l’integrale erano ancora comprensibili solo come calcolo della tangente e dell’area). La matematica, tuttavia, non doveva più rispecchiare la realtà, ma, almeno nella Mitteleuropa, si andava organizzando in teorie, strutture linguistiche complesse, autonome anche dalle teorie fisiche. I segni, che fino al Settecento erano solo uno strumento di calcolo, diventavano sempre più un linguaggio di rappresentazione della scienza matematica e naturale. Gli enti matematici conservavano i loro caratteri intuitivi e costruttivi geometrici, e tuttavia assumevano sempre più una caratterizzazione algebrica. Era questa che, in definitiva, ne determinava l’identità e le relazioni, e questa evoluzione implicava la crescente centralità di concetti quali le corrispondenze biunivoche, gli isomorfismi, le trasformazioni.

La matematica assumeva un aspetto più concettuale, non più limitata a enti evidenti all’intuizione e ai calcoli/teoremi a essi relativi: i concetti matematici diventavano i veri oggetti della analisi. Nozioni fondamentali, quali grandezza, numero, continuo, infinito, spazio, misura, che fino al Settecento avevano un carattere non problematico e descrittivo (anche se di una realtà ormai accessibile solo in laboratorio), cominciavano a diventare problematiche, a richiedere una ricostruzione su basi di tipo logico e insiemistico, mentre le loro proprietà si traducevano in definizioni e in assiomi su cui edificare le teorie.

L’autonomia e centralità del registro sintattico caratterizza soprattutto l’analisi nella prima metà del secolo. Lo iato tra la matematica e la fisica si tradurrà invece in una crescente distinzione tra sintassi e semantica, particolarmente rilevante nella trasfigurazione di algebra e geometria nella seconda metà del secolo. L’autonomia della sintassi e la distinzione tra sintassi e semantica diventeranno il dato caratterizzante della matematica moderna. Dall’autonomia della sintassi derivava lo studio di funzioni definite solo formalmente (tramite integrali o serie, quali le funzioni ellittiche, ipergeometriche ecc.), del tutto estranee all’idea di funzione come espressione; da questa impostazione scaturiva anche il problema dell’esistenza (in un senso da stabilire) degli enti matematici. La stessa corrispondenza tra curve ed equazioni, che il Settecento aveva visto come naturale, appariva più complessa: la curva di fig. 32,

pur non avendo un’espressione unica (uguale a e^x per x negativo, e^−x per x positivo), era l’integrale di un’unica espressione:

In questa prospettiva emerge anche la questione dei fondamenti della matematica, termine chiave della filosofia kantiana che avrà un ruolo centrale dalla fine dell’Ottocento a oggi. La questione nasceva dal venir meno dei due capisaldi su cui aveva poggiato in passato l’indiscutibilità dei fondamenti della matematica: da un lato la sua “certezza” razionale, fondata sull’idea di dimostrazione euclidea a partire da assiomi evidenti, dall’altro il suo legame indissolubile con la stessa realtà naturale. Se la distinzione tra sintassi e semantica metteva in discussione questo legame, parallelamente faceva della dimostrazione e della sua certezza un fatto sempre più solo formale. Così l’analisi, presentata con frequenza sempre maggiore attraverso il simbolismo algebrico, non poteva più fondarsi né sui successi della fisica né sull’evidenza delle dimostrazioni geometriche, svincolata ormai dall’essere semplice riflesso formale e necessario di una realtà “data”. Occorreva un fondamento degli stessi aspetti formali non riducibile alla credibilità o evidenza degli assiomi. Il tema appare in diversi autori, tra i quali Bernhard Bolzano (1781-1848), che sottolinea l’insufficienza del rigore geometrico per fondare l’analisi. La stessa geometria, diventando sempre più solo la dottrina dello spazio, si doveva porre il problema dei propri fondamenti epistemologici, mentre il linguaggio algebrico-aritmetico sempre più diventava la base del fondamento logico rigoroso di tutto il pensiero matematico.

Il trattamento geometrico-meccanico della natura fisica, tipico della scienza del Seicento in cui la geometria rappresentava immediatamente e iconicamente la realtà, non era più sufficiente a fondare la matematica, che costituiva ormai un universo autonomo, per nulla “simile” alla realtà, e la cui assimilabilità alla natura fisica passava per una inedita centralità del kantiano soggetto della conoscenza. Platone sosteneva (secondo Plutarco) e Keplero ripeteva, che «dio geometrizza», Gauss (secondo Kronecker) sosteneva che «dio aritmetizza», e Dedekind correggerà in «l’uomo aritmetizza».

La sintassi dimorava sempre più dentro l’attività creatrice del soggetto, la semantica riguardava invece le scienze naturali. Le coordinate cartesiane, che in Cartesio erano ancora intrinseche e immanenti nella figura, nel Settecento diventano estrinseche e traccia del soggetto della fisica-matematica (il sistema di riferimento degli assi cosiddetti cartesiani), formando un autentico panoptikon, il soggetto capace di descrivere compiutamente l’universo newtoniano, e, secondo Laplace, con la meccanica newtoniana anche di prevederne il futuro e conoscerne il passato. Ma la stessa conoscenza empirica appariva limitata a una descrizione relativa e soggettiva del mondo: Hume aveva sottolineato come la stessa idea di causalità fosse solo legata alla connessione temporale degli eventi consolidatasi nell’abitudine. La scienza per contro richiedeva di essere intersoggettiva; appariva quindi necessario fissare le caratteristiche che doveva avere una scienza invariante rispetto al cambiamento del soggetto. Di quella soggettività e di questa intersoggettività Kant era stato in un certo senso il padre, chiarendo che la “certezza” della matematica non aveva niente a che fare con l’oggettività o la razionalità dei suoi assiomi. In verità, egli era rimasto legato al senso geometrico della fisica newtoniana e abbastanza cieco nei confronti delle potenzialità della logica; ciò lo aveva portato a ritenere ormai chiusa e completa la logica formale e ad ascrivere un carattere a priori alla geometria euclidea: nel Settecento la logica appariva periferica alla ricerca scientifica e il significato geometrico della fisica-matematica era ancora dominante.

Nell’Ottocento il soggetto trascendentale kantiano diventa creatore della ragione scientifica, ma il soggetto empirico (il sistema di riferimento) appare relativo: di qui la centralità dello studio teorico delle proprietà invarianti per una data trasformazione di tale sistema. Si capovolge il legame settecentesco tra geometria e fisica: lo spazio non è più il palcoscenico assoluto delle leggi fisiche e del sistema del mondo newtoniano, bensì ne diventa un aspetto, e certe caratteristiche di invarianza, omogeneità e simmetria dello spazio si traducono in principi di conservazione di quantità fisiche. La relatività sia speciale sia generale segnerà il coronamento di questa nuova relazione tra geometria e fisica.

Gauss

La moderna idea di spazio era emersa con il concetto di continuo aritmetico infinito. Per Newton lo spazio era quasi il sensorium divino, per Kant la geometria e la percezione spazio-temporale si presentavano come condizioni a priori della scienza. Nell’Ottocento lo spazio geometrico resta lo sfondo oggettivo e reale di tutta la fisica, ma comincia ad assumere i caratteri di una generica varietà n-dimensionale: un concetto molto ampio in cui il carattere intuitivo dello spazio si generalizza in termini di dimensioni, di curvatura, di proprietà invarianti e di trasformazioni caratterizzate algebricamente, mentre la matematica ottocentesca trova sempre più la sua dimora nel soggetto e nella sua attività creatrice. Si esalta il carattere mentale degli enti matematici, se ne cerca la radice nella ragione umana e si pone il problema della sua autonoma struttura linguistica. Di conseguenza il baricentro della matematica si sposta: non è più la geometria, ma diventa sempre più la manipolazione algebrica, riflesso simbolico dell’aritmetica, la quale fino ad allora era rimasta solo calcolo, una parte secondaria e sostanzialmente pratica della matematica; anche in Kant essa non aveva assunto una fisionomia molto precisa, pur apparendo, almeno nell’analisi del numero cardinale, fondata su giudizi sintetici. Scrive invece Gauss che «dobbiamo umilmente ammettere che, mentre il numero è un prodotto del nostro spirito, lo spazio ha una realtà esterna alla nostra mente, così che noi non possiamo completamente prescrivere le sue proprietà a priori»: è cioè nell’aritmetica che si sviluppa compiutamente la libertà creatrice dello spirito umano, e non nella geometria, connessa e vincolata non solo alla percezione, ma anche a un necessario accordo con la realtà esterna e quindi assimilabile alla meccanica.

Carl Friedrich Gauss (1777-1855) non si occupò di fisica-matematica in senso stretto: la sua opera più celebre, le Disquisitiones arithmeticae, parte dalla teoria delle congruenze modulo per sviluppare una lunga serie di capitoli della teoria dei numeri; come astronomo è famoso per la sua capacità di dedurre matematicamente le orbite dei corpi celesti dalle osservazioni. Introdusse anche lo studio statistico degli errori e della loro distribuzione (la gaussiana). La matematica assume ormai in Gauss i caratteri di uno strumento che il soggetto conoscente usa per descrivere il mondo fisico, ed è oggetto autonomo di analisi, poi applicabile alla fisica. L’analisi, per esempio, si concentra sulle serie di potenze come oggetti formali, e sul loro collegamento con le equazioni differenziali e il calcolo degli integrali. Gauss intuisce l’importanza della notazione matematica, della sua profonda differenza da quella degli antichi e di come essa sia una leva per risolvere problemi complessi, ma vede il rischio di una riduzione meccanica del suo uso, quale si era affermata nel calculus settecentesco, e richiede che sempre se ne mantengano i caratteri concettuali originali; un esempio è fornito dalle serie, le quali hanno un significato chiaro quando convergenti, ma non quando divergenti: «Appena una serie cessa di essere convergente, la sua somma in quanto somma non ha significato», e questo porta anche a diffidare dell’infinito, semplice «façon de parler».

In geometria Gauss inizia lo studio intrinseco delle superfici. Già Eulero si era reso conto del fatto che una superficie nello spazio, descritta con una equazione F(x, y, z) = 0 in R³, poteva anche essere studiata associando a ogni punto una coppia di coordinate sulla superficie u(x, y, z), v(x, y, z) (per esempio latitudine e longitudine su una superficie sferica). È questa l’idea di una geometria intrinseca: una superficie nello spazio euclideo può così essere studiata “dall’esterno” tramite la sua equazione, oppure la si può considerare in sé, definendo la sua metrica locale descritta in termini di coordinate intrinseche da un differenziale ds² = Edu ² + 2Fdudv + Gdv ², dal quale ricavare le sue proprietà geometriche. Per esempio la curvatura della superficie (concetto che emerge intuitivamente dalla rappresentazione tridimensionale) poteva essere determinata anche da tale metrica intrinseca (e quindi da misure locali) e restare invariante per qualunque trasformazione della superficie che non ne provocasse pieghe o strappi (per esempio la superficie laterale di un cilindro o di un cono poteva essere trasformata in una superficie piana preservandone la metrica, cosa impossibile invece per una superficie sferica).

Le geometrie non euclidee

Un altro capitolo della matematica ottocentesca legato al nome di Gauss è quello delle geometrie non euclidee. Ufficialmente la loro scoperta è attribuita a János Bolyai (1802-60) e Nicolaj Ivanovič Lobačevskij (1793-1856), ma ci sono evidenze che Gauss, ben prima di questi, ne avesse studiato i caratteri principali. Tali geometrie mettevano fine ai tentativi susseguitisi fin dall’antichità di dimostrare il postulato delle parallele dagli altri postulati della geometria euclidea. In particolare nella prima metà del Settecento Giovanni Girolamo Saccheri (1667-1733) aveva tentato di dimostrare il postulato per assurdo studiando le conseguenze della sua negazione, e trovando una lunga serie di teoremi strani, ma non assurdi (per esempio: la somma degli angoli interni di un triangolo differiva da 180° di una quantità crescente con l’area del triangolo e i triangoli simili erano anche uguali).

Una difficoltà nasceva dal fatto che le geometrie ellittiche (per le quali non esistono rette parallele a una retta per un punto esterno a essa) hanno un modello banale (la superficie di una sfera, dove le rette sono costituite dai cerchi massimi, le cui proprietà erano note già ai greci nella trigonometria sferica, fig. 33), ma sembrano violare il secondo postulato di Euclide, secondo il quale le linee rette sono illimitate. In realtà la geometria ellittica soddisfa il secondo postulato se lo si intende come richiesta che le rette siano illimitatamente prolungabili (anche se finite, come gli archi dei cerchi massimi sulla sfera) invece che tout court infinite: distinzione questa che verrà in seguito sottolineata da Riemann. Le geometrie iperboliche, invece (per le quali esistono infinite parallele a una retta per un punto esterno a essa) rispettano tale postulato ma non ammettono modelli semplici.

Gauss aveva intuito che non era scontata la kantiana necessità a priori della geometria euclidea in quanto non dimostrabile, anzi essa appariva piuttosto a posteriori (e affine alla meccanica), mentre l’essere a priori sembrava piuttosto una caratteristica dell’aritmetica. Si è molto sottolineato il carattere “antikantiano” delle geometrie non euclidee, ma Gauss non colse mai tale carattere, pur avendo studiato attentamente Kant. Di fatto era stato proprio Kant ad aprire la frattura tra realtà esterna e formalismo matematico, e anche nello spostamento dell’a priori dall’intuizione spaziale alla creatività del soggetto nell’aritmetica, Gauss riecheggiava in realtà la connessione kantiana tra tempo e struttura del soggetto della conoscenza. Le geometrie non euclidee nell’Ottocento non destarono inizialmente una grande impressione e sembrarono solo una curiosità. Col tempo risultò chiaro che si trattava di una geometria diversa da quella euclidea ma altrettanto rigorosa e coerente (si costruirono modelli euclidei anche della geometria iperbolica), e diventarono l’esempio paradigmatico della fine della sovrapponibilità di sintassi e semantica che aveva caratterizzato la matematica fino al Settecento.

Gauss dimostra anche finalmente in maniera rigorosa il teorema fondamentale dell’algebra (ogni polinomio di grado n ammette almeno una radice complessa e di conseguenza ne ammette n) tramite la rappresentazione geometrica dei numeri complessi, introdotta nel Settecento da Eulero, per connettere i numeri complessi alla trigonometria: e^ix = cosx + i sinx, dove e è la costante di Eulero, base dei logaritmi naturali. Di qui derivava una rappresentazione geometrica sul piano, in cui e^ix è un vettore unitario di inclinazione x, del quale cosx è la parte reale e sinx la parte immaginaria (fig. 34).

Tale formula per x = π diventa e ^iπ = −1, giudicata quasi universalmente “la più bella formula matematica di sempre” perche coniuga in poco spazio le più importanti costanti matematiche.

In Gauss la geometria non è più la scienza dell’essere e il paradigma della ragione deduttiva: la sua metamorfosi ha ormai avuto inizio.

La matematica nelle università

Il passaggio tra Settecento e Ottocento è segnato anche dalla trasformazione delle università che assumono la loro forma moderna. La seconda metà del Settecento aveva visto affiancarsi alle accademie come luoghi di attività dei matematici le scuole ingegneristiche militari, in cui la matematica applicata alla meccanica aveva un ruolo centrale. Con la rivoluzione francese e poi con Napoleone questa vocazione ingegneristica e militare della matematica si accentua: è in gran parte la matematica applicata a caratterizzare l’École polytechnique della riforma napoleonica, nella quale insegnano alcuni dei massimi matematici dell’epoca, da Monge a Legendre, da Lagrange a Fourier. Nasce in questo periodo la figura del professore di matematica. La caduta di Napoleone non interrompe lo sviluppo dell’insegnamento matematico nelle università, anche quando nel corso del secolo il baricentro della ricerca matematica si muove dalla Francia verso la Germania, spostamento questo che segnerà anche la nuova stagione del pensiero matematico: in antitesi alla fisica-matematica e al legame con le applicazioni ingegneristiche tipiche del Settecento francese si delinea una matematica pura, autonoma, che caratterizzerà la scienza moderna fino a oggi.

L’aritmetizzazione della analisi

Protagonista degli inizi dell’Ottocento è la figura e l’opera di Jean-Baptiste-Joseph Fourier (1768-1830), in cui il rapporto intimo tra fisica e matematica tipico del Settecento francese si estende al di là della semplice meccanica per investire tutta la fisica, in particolare la teoria del calore, che comincia a saldarsi con la meccanica: si delinea l’idea che il calore stesso sia una forma di energia, la cui conservazione, nelle diverse forme in cui essa si trasforma, diventa uno dei principi fondamentali della fisica. In Fourier tuttavia matematica e fisica appaiono più autonome: la connessione si realizza nell’applicazione degli strumenti matematici alle condizioni fisiche. Il risultato più importante di questa connessione è la teoria delle serie di Fourier.

Punto di partenza è lo studio delle equazioni differenziali che caratterizzano la diffusione del calore nei solidi. Lungo una sbarra infinita l’equazione è, detta ν la temperatura:

Il calcolo della somma della serie è effettuato sulle somme parziali di n termini di una serie trigonometrica e poi esteso al limite per n → ∞, mentre la natura fisica del problema fornisce un criterio di selezione di soluzioni e procedure: il problema della convergenza, sebbene non ancora matematicamente esplicito, è già presente.

Le serie trigonometriche erano già apparse nello studio delle corde vibranti, e del resto le funzioni seno e coseno hanno la caratteristica (utilissima nelle equazioni differenziali e sostanzialmente condivisa da esponenziali e polinomi) di avere derivate di qualsiasi ordine sempre dell’identico tipo. Non è quindi strano che esse appaiano nell’Ottocento uno strumento cruciale per la risoluzione di tali equazioni. La forma più nota di serie di Fourier è

nella quale i coefficienti sono calcolabili dalla stessa ƒ(x):

e risulta quindi naturale chiedersi se ogni funzione possa essere scritta come serie trigonometrica, questione resa più complessa anche dal fatto che la trasmissione del calore, diversamente dal comportamento delle onde vibranti, non ha carattere ondulatorio: disomogeneità tra fisica e matematica impensabile nel Settecento, ma normale nell’Ottocento. Il risultato fondamentale di queste ricerche è che praticamente qualsiasi funzione periodica ƒ(x) può essere scritta come serie di Fourier o, se non periodica, come integrale:

In questa forma entra in crisi l’idea settecentesca di funzione come espressione algebrica, e anche l’idea di continuità inizia a trasformarsi, sebbene solo con Cauchy si delineerà la concezione moderna.

L’autonomia della sintassi in analisi si traduce nello spostamento dell’attenzione dall’uso degli oggetti del calcolo, considerati quasi naturali nell’analisi settecentesca (funzioni, continuità, serie, successioni, differenziali, integrali), alla definizione e caratterizzazione rigorosa degli stessi e delle loro mutue relazioni, distinta dalla loro applicazione.

Il calcolo differenziale, che fino all’inizio dell’Ottocento trovava ancora l’unico suo possibile senso nel modello geometrico, sebbene avesse ormai acquisito un linguaggio puramente algebrico, entra in una fase generalmente nota come aritmetizzazione dell’analisi che darà al calcolo la sua forma moderna, basata sul linguaggio algebrico e sulla traduzione statica del concetto di limite. Viene data una definizione rigorosa dei concetti di derivata e integrale, e vengono chiariti i concetti di infinito, convergenza e continuo, che avevano un ruolo cruciale nella matematica moderna ma che erano ancora rimasti poco più che una intuizione geometrica.

Va sottolineato come l’espressione orale del nuovo simbolismo dell’analisi abbia ancor oggi un carattere dinamico (limite, converge, tende a...) derivato dalle serie e dalla tradizione newtoniana, mentre le definizioni formali hanno un carattere statico, più vicino al formalismo dei differenziali leibniziani. Un’ambiguità che sopravvisse anche a livello concettuale fino a che Karl Weierstrass (1815-97) non dette del concetto di limite di una funzione la definizione statica attuale («per ogni ε positivo esiste un δ tale che…»).

Quest’approccio appare già nell’opera di Bolzano, ma è nel 1821 che si inaugura il “nuovo corso” dell’analisi, con il Cours d’analyse algébrique et infinitésimale di Augustin-Louis Cauchy (1789-1857), nel quale tuttavia rimane ancora notevole il ruolo dell’intuizione geometrica del rapporto tra continuo geometrico e continuo aritmetico.

L’esigenza di una chiarificazione concettuale nasceva anche dall’osservazione della non coincidenza nel comportamento tra una funzione e la sua definizione analitica infinita (sia nelle serie di Taylor sia nelle serie di Fourier). Innumerevoli esempi mostravano infatti che non sempre e ovunque la serie relativa alla funzione ƒ(x) convergeva a ƒ(x): la coincidenza tra le due si realizzava solo se le variabili cadevano in certi intervalli. Era il problema della convergenza della serie. Al di fuori di tali intervalli di convergenza le serie divergevano, assumendo valori diversi dalla funzione: per esempio la serie geometrica

converge per x < 1 e il valore della serie coincide con quello della funzione, per x = 1 assume un valore infinito tanto la funzione quanto la serie, ma per x > 1 la serie assume un valore infinito mentre la funzione assume valori finiti: per esempio per x = 2 si ha 1 + 2 + 4 + 8 + 16 + ... = −1. Scrive Cauchy: «Una serie divergente non ha somma». L’autosufficienza del registro simbolico affermatasi con Lagrange non garantiva il rigore.

Lo stesso concetto di funzione doveva essere generalizzato: le serie di Fourier risultano capaci di caratterizzare funzioni non esprimibili con le normali espressioni finite. Cauchy introdusse l’idea che una funzione fosse una relazione qualsiasi tra due variabili, ma pensava solo a funzioni implicitamente definite da un sistema di equazioni non risolubile. Solo con Johann Peter Gustav Dirichlet (1805-59) si afferma la nozione moderna di funzione, y = ƒ(x), come qualsiasi “legge” che al valore di una variabile x associa quello di un’altra variabile y, con esempi anomali quali la funzione di Dirichlet, che vale 0 quando x è razionale e 1 quando x è irrazionale, e della quale non sembrava immaginabile né una presentazione geometrica né una espressione algebrica (neanche infinita).

Il concetto di limite si precisa nello studio delle serie e delle sequenze numeriche a_n al crescere di n verso l’infinito (esperienza comune era l’approssimazione sempre più precisa di un numero irrazionale tramite numeri razionali). Per Cauchy «una serie è convergente se per valori crescenti di n la somma parziale s_n dei primi n termini si avvicina indefinitamente al limite s […] è necessario e sufficiente che per valori indefinitamente grandi di n le somme s_m con m > n, differiscano dal limite s, e quindi tra di loro, di quantità infinitesime».

La nuova caratterizzazione della continuità di ƒ in x è data dal fatto che la differenza ƒ(x + h) − ƒ(x) decresca infinitamente al decrescere di h a zero, tanto per h positivo che negativo. L’infinitesimo non è più una costante infinitamente piccola, ma solo un valore numerico variabile, e Cauchy aggiunge «il cui limite era zero», adoperando ancora una intuizione “dinamica”. È un’idea di continuità del tutto diversa da quella lagrangiana: anche curve spezzate ma tali, per così dire, che i diversi pezzi si incollino in un punto comune possono essere continue (come nella fig. 32).

La definizione attuale di continuità di una funzione ƒ(x) in x₀ richiede che per ogni ε positivo esista un δ tale che per ogni x per cui |x − x₀| < δ si abbia che |ƒ(x) − ƒ(x₀)| < ε, ci debba essere cioè una variazione infinitesima della ƒ(x) per ogni variazione infinitesima della x. La definizione rigorosa sarà formulata da Riemann e Weierstrass poco dopo la metà del secolo. In precedenza si trattava di un teorema o un’idea intuitiva, in quanto si concepiva la continuità ancora legata all’idea geometrica di una curva connessa, senza cioè interruzioni nel suo tracciamento. Questo mutamento con cui si affermavano le concezioni moderne di funzione e di continuità segnava così la fine definitiva di un fondamento geometrico per le idee della analisi, ed è significativo che questa crisi si risolva in Riemann, lo stesso autore che porrà in forma nuova il problema del fondamento delle idee di base della geometria.

L’espressione di una funzione tramite le serie diventa infinita, e il processo non è indolore. Per esempio si consideri la serie di Maclaurin per ƒ(x):

esistono casi in cui essa converge ma non a ƒ(x), e addirittura casi in cui pur essendo tutti i termini ƒ⁽ⁿ⁾(0) nulli la ƒ(x) non è identicamente nulla

(fig. 35).

Già Bolzano e poi Riemann e Weierstrass daranno anche esempi di funzioni continue ma non derivabili in nessun punto, per esempio:

Inoltre per Cauchy la somma di serie di funzioni continue doveva essere continua; essendo seno e coseno continue, la somma di una serie di Fourier dovrebbe essere sempre continua, ma anche in questo caso appaiono controesempi. Vi sono infatti curve (fig. 36) che, pur essendo discontinue, possono essere espresse come serie di Fourier.

Ma il ragionamento di Cauchy richiedeva implicitamente che lo scarto tra la funzione somma totale e le funzioni somme parziali della serie dovesse essere un infinitesimo indipendente dal valore della x (la convergenza uniforme: in un dato intervallo, per ogni ε positivo esiste un numero n non dipendente da x tale che per m > n e per ogni x: |s_m(x) − s(x)| < ε). La sua dimostrazione dipendeva invece dalla intuizione geometrica di curve la cui differenza diventava in ogni punto sempre minore e che quindi al limite dovevano coincidere, cosa che accade però solo quando la convergenza non risulti infinitamente lenta in qualche punto dell’intervallo considerato, sia cioè uniforme.

L’idea di convergenza uniforme rispondeva alla scoperta di serie che in punti isolati mostravano un comportamento patologico. Negli intorni dei punti in cui la convergenza non era uniforme, le relazioni tra convergenza, continuità, integrabilità, differenziabilità delle serie risultavano molto complesse, e il loro studio richiedeva l’abbandono dell’intuizione geometrica e lo sviluppo di standard di rigore puramente logici. Si trattava allora di trovare in quest’ambito le mutue relazioni sussistenti tra la intuizione geometrica di continuità, la convergenza delle serie e la derivabilità, analizzando, in un modo quasi empirico, tali funzioni “patologiche”.

L’estensione del concetto di integrale

Nel Settecento l’integrale era l’operazione inversa della derivazione, e l’integrale definito era costruito come differenza tra i valori dell’integrale indefinito calcolati sugli estremi dell’intervallo. Ma l’integrale definito poteva essere calcolato anche su funzioni di cui si ignorava la primitiva, e Cauchy lo definisce come limite comune della somma dei rettangolini infinitesimi inscritti e circoscritti alla curva (fig. 37).

In realtà si tratta di un recupero dell’idea originaria (prima metà del xvii secolo) di integrale definito inteso come quadratura di una curva, ma è anche il punto di partenza della teoria della misura: è l’integrale indefinito a diventare allora un integrale definito con l’estremo superiore variabile.

Nei decenni successivi la definizione di integrale si estende a funzioni sempre più “patologiche”, dotate cioè di punti di discontinuità o estremali in numero anche infinito. Dirichlet applica il concetto di integrale a funzioni con infiniti punti di discontinuità e dimostra la convergenza delle serie di Fourier (ma presto se ne troveranno controesempi). Si costruiscono inoltre funzioni altamente patologiche, come la funzione di Dirichlet, nella quale esiste un insieme infinito di punti di discontinuità, addirittura coincidente con l’insieme dei reali, e non esiste nemmeno un intervallo in cui essa sia continua: infatti non solo tra ogni due razionali distinti esistono infiniti irrazionali ma anche che tra due irrazionali distinti esistono infiniti razionali. Ma l’infinito trattato sintatticamente si rivelava un “luogo” veramente strano non solo per le serie di funzioni, ma anche per le ordinarie serie numeriche. Per esempio consideriamo la serie convergente

Se la dividiamo per 2 otteniamo

Ora sommiamo le due serie, raggruppando opportunamente i termini: i termini con denominatore dispari restano invariati; sommiamo a coppie i termini con uguale denominatore multiplo di 4 e infine cancelliamo (poiché appaiono con segni opposti) i termini con uguale denominatore pari ma non multiplo di 4: sorprendentemente troviamo la serie di partenza, così che 3/2ln2 = ln2!

Un’indagine più attenta rivela che l’assurdo deriva dall’aver usato la proprietà commutativa su infiniti termini della serie, e un teorema dimostrerà che questo si può fare solo per serie assolutamente convergenti (converge anche la serie dei valori assoluti dei termini della serie iniziale). Su serie convergenti ma non assolutamente convergenti l’uso della proprietà commutativa su infiniti termini permette di ottenere come somma qualsiasi valore! La serie nell’esempio infatti era convergente, ma la serie dei suoi valori assoluti era la serie armonica, 1 + ½ + ¹/₃ + ¼ +…+ ¹/n …, divergente.

Il teorema chiarisce il fenomeno, ma resta il fatto paradossale che l’estensione per analogia all’infinito di una delle più fondamentali proprietà della somma risulta impraticabile, al punto che la stessa idea di somma di una serie convergente risulta dipendente dall’ordine tipografico di scrittura della serie stessa.

La definizione di funzione come legge generica sui reali appariva però nel contempo troppo generale e troppo limitata. Una definizione più utile si poteva dare considerando la funzione analitica di variabile complessa, definita come una serie di potenze convergente in un dominio complesso, un oggetto puramente simbolico e privo di senso geometrico intuitivo, ma dalle proprietà affascinanti.

In Cauchy il senso degli enti matematici dell’analisi era in fondo ancora geometrico, ma il simbolismo era pienamente autonomo, e questo gli consentiva di studiare tali funzioni.

Lo studio delle funzioni di variabile complessa raggiunge la sua forma moderna in Bernhard Riemann (1826-66). Se si considera che il numero complesso z = x + iy può essere rappresentato sul piano dal punto di coordinate (x, y) e il numero z + dz = x + dx + i(y + dy) dal punto (x + dx, y + dy), si ha che dz = dx + idy è un cammino infinitesimo nel piano congiungente i due punti z e z + dz. È evidente che un integrale definito fra due numeri complessi corrisponde allora a un generico cammino sul piano fra i due punti corrispondenti e non è univocamente determinato; occorre quindi, per definire univocamente la derivata di una funzione w(z) = u(z) + iv(z), che la differenziazione non dipenda da tale cammino, e questo corrisponde a richiedere le condizioni di olomorfismo:

Anche queste erano condizioni già studiate da Cauchy, ma in Riemann sono alla base di una delle teorie più eleganti e potenti della matematica moderna. Le funzioni olomorfe sono infatti infinitamente differenziabili e analitiche, e il calcolo differenziale e integrale su di esse assume una serie di proprietà semplici ed eleganti. Caratteristico della teoria di Riemann è l’intreccio che si stabilisce tra intuizione geometrica e studio puramente algebrico, un intreccio caratteristico della matematica della seconda metà dell’Ottocento, in cui aspetti algebrici caratterizzano enti concettualmente di origine geometrica.

Il numero reale e il continuo

Lo studio di funzioni e insiemi costruiti in maniera puramente formale e la scoperta di oggetti patologici sono l’effetto del passaggio definitivo da un’analisi fondata sull’intuizione geometrica a un’analisi fondata sul rigore logico e sui concetti algebrico-aritmetici, che appare come «una matematica puramente concettuale, sganciata da ogni intuizione» (Hankel).

L’esempio più lampante è il concetto di numero reale, emerso all’inizio del Seicento negli «infiniti gradi di tarditate» nel moto dei gravi di Galileo, nella infinita scrittura decimale di Stevin, nella corrispondenza tra numeri e punti di Cartesio, e fondamento dell’analisi, senza che nessun matematico sentisse l’esigenza di darne una definizione finché era intuitivamente riducibile al concetto di punto. Ma una tale intuizione nell’Ottocento si era rivelata insufficiente: di qui la necessità di una sua caratterizzazione aritmetica.

Nella seconda metà dell’Ottocento ne vengono proposte diverse definizioni, concettualmente differenti ma logicamente equivalenti. Julius Wilhelm Richard Dedekind (1831-1916) lo fa riprendendo una delle antiche caratterizzazioni aristoteliche del continuo: ogni dicotomia ha un elemento di separazione comune a entrambe le parti. Più precisamente egli cerca di costruire i reali sulla retta partendo dalla costruzione su di essa dei razionali, già nota a Euclide, basandosi sulla definizione eudossiana di uguaglianza dei rapporti. Costruiti i punti razionali sulla retta, ne effettua una sezione, cioè una dicotomia in due classi tali che ogni elemento dell’una sia minore di ogni elemento dell’altra, e associa a tale sezione un numero reale. Vi può essere così una sezione in cui un numero razionale è il minimo della classe maggiore (o il massimo di quella minore), ed essa può identificarsi con tale razionale. Ma vi sono sezioni in cui un tale razionale non esiste, per esempio quella in cui le due classi sono i razionali x tali che x ² sia rispettivamente maggiore o minore di 2: esse possono essere identificate con gli irrazionali (nell’esempio √(2)). La continuità per Dedekind è allora caratterizzata dalla proprietà che ogni sottoinsieme dotato di una limitazione superiore (o inferiore) ammetta una minima limitazione superiore (o inferiore). In tal caso si può definire una corrispondenza biunivoca tra i punti della retta continua e le sue sezioni: sull’insieme dei numeri razionali le sezioni determinano nuovi numeri, quelli reali, sull’insieme dei numeri reali le sezioni non definiscono nuovi numeri, l’insieme è completo. Il continuo non è più un attributo qualitativo intuitivo, bensì la caratterizzazione di un insieme completo, massimale, chiuso per l’estensione transfinita della procedura di costruzione del minimo della sezione, oggetto quindi di una costruzione infinita in senso aritmetico o insiemistico, frutto della potenza creatrice del pensiero umano. Dedekind mostra anche come il concetto di continuo sia in realtà indipendente dalla geometria di Euclide, che ammetteva anche modelli non continui, ossia insiemi discontinui (costruiti con lunghezze date da numeri algebrici) che soddisfacevano tutti i teoremi di Euclide. Niente di strano quando si ricordi la natura fisica del concetto di continuo fino al medioevo, ma decisamente sorprendente quando si ricordi come tutta la dottrina del continuo numerico fosse stata basata sul presupposto di una ovvia e necessaria continuità della geometria euclidea: sino ad Aristotele, era stata la grandezza geometrica l’unica realtà continua (con il tempo). Era questo presupposto che aveva garantito l’“esistenza” dei numeri irrazionali ottenuti come limiti di sequenze convergenti di razionali fino a Cauchy. Questi aveva considerato i numeri reali come «limite delle diverse frazioni che ne forniscono valori sempre più approssimati», dando così già implicitamente per esistente il limite (e quindi l’oggetto da definire) e tematizzabile solo la sua unicità: si trattava di una definizione circolare e di un errore logico notato da Weierstrass, un circolo vizioso che emergeva quando veniva meno l’intuizione geometrica che garantiva la corrispondenza tra punti e numeri reali.

Georg Cantor (1845-1918) invece definirà la successione fondamentale {a_i} tramite la condizione che, per ogni ε e per ogni m, esiste un n tale che |a_m − a_n| < ε (garantendo così la convergenza senza dover già ipotizzare l’esistenza del limite) ricorrendo alla nozione di equivalenza tra successioni fondamentali {a_i′} e {a_i} (quando per ogni ε esiste un n tale che per ogni m > n: |a_m − a_m′| < ε) per definire il numero reale come associato a una delle successioni fondamentali equivalenti.

Queste definizioni non erano sufficienti però a dimostrare l’intuizione fondamentale su cui era cresciuta l’idea di numero reale per due secoli: la corrispondenza biunivoca tra il continuo geometrico, la retta e il continuo aritmetico, l’insieme dei numeri reali (unica eccezione concepibile gli eventuali infinitesimi aritmetici, che erano tuttavia svaniti con Weierstrass). Si riusciva ora a dimostrare che a ogni punto si poteva associare un numero reale, ma il viceversa doveva essere postulato con un assioma di continuità.

I fondamenti della geometria

La geometria non metrica di Euclide aveva lasciato il posto nel Settecento a una geometria “euclidea” metrica e meccanica. Nell’Ottocento gli aspetti metrici tendono a venire assorbiti nella caratterizzazione fisica dello spazio; così l’aritmetizzazione e l’algebrizzazione dell’ analisi affermatesi definitivamente nell’università di Berlino con Kronecker e Weierstrass vengono talora vissute come un’emarginazione della geometria. Ma la polemica ricorrente nell’Ottocento tra sostenitori dell’approccio sintetico e sostenitori di quello analitico (o tra difensori dell’intuizione geometrica e paladini del rigore logico-algebrico) nasconde una sottile convergenza fra i due orientamenti, spesso mediata da questioni di fisica, un aspetto molto rilevante in un autore come Riemann.

Per alcuni decenni nella prima metà del secolo, a fronte dei progressi dell’analisi, la geometria quasi scompare, per riapparire poi del tutto trasformata nella seconda metà dell’Ottocento: tramonta la classica geometria euclidea e newtoniana, presentazione naturale della realtà fisica, appare invece un sistema di geometrie con cui trattare tutti i concetti di origine geometrica, che coinvolge le tecniche analitiche ma non si riduce a esse. Non si tratta soltanto della risposta a un’esigenza di rigore quanto piuttosto di un cambiamento radicale della stessa concezione della disciplina: l’attenzione si sposta dallo studio degli oggetti geometrici (intesi come naturali nella geometria euclidea o come ipotetici in quella non euclidea) alla loro caratterizzazione algebrica e formale (dualità, trasformazioni, assiomi) e all’analisi del rapporto tra la loro caratterizzazione teorica e le conseguenti proprietà dello spazio fisico (corpi rigidi, proprietà invarianti, misura). I concetti della geometria del xix secolo mantengono così le loro radici nell’intuizione geometrica ma la sviluppano analiticamente e logicamente. In tal modo la geometria non è più né il rispecchiamento della realtà naturale né l’espressione della connessione tra necessità matematica e realtà meccanica, ma il punto di contatto tra l’intuizione spaziale a priori e un soggetto trascendentale logico e algebrico, un nodo di proprietà fisiche e intuitive da dipanare sintatticamente.

Il concetto di spazio

L’analisi del continuo aritmetico aveva fatto del continuo solo un frutto della capacità creatrice dell’uomo; restava l’esigenza di analizzare il concetto di spazio e di capire che collegamento ci fosse tra la creatività della mente e lo spazio fisico esterno.

Il rapporto tra la forma spaziale a priori dell’intuizione e la struttura teorica della geometria era stato al centro della filosofia kantiana. Dopo Kant la caratterizzazione sempre più aritmetica del continuo aveva trasformato profondamente la questione aprendo la via all’analisi di Riemann, espressa nella sua dissertazione del 1854 sulle ipotesi alla base della geometria, nella quale sviluppava anche l’analisi della metrica intrinseca, iniziata da Gauss. Lo spazio non era più lo spazio assoluto di Newton. Il Theorema Egregium di Gauss asseriva che la curvatura di una superficie era una proprietà intrinseca, poteva cioè essere calcolata punto per punto da misure di distanze e angoli sulla superficie stessa, senza riferimento alla sua collocazione nello spazio, e questo dimostrava che il soggetto della conoscenza poteva essere locale, privo cioè della capacità di osservare tutto lo spazio, ma in grado di costruire la sua geometria e la sua fisica a partire da una percezione locale di esso.

Per Riemann (come per Dedekind) la struttura assiomatica doveva avere le sue radici in un’analisi dei concetti di base, in un certo senso “esplicitarne” la definizione. Inoltre gli assiomi della geometria non dovevano derivare dall’idea generica di spazio e di estensione; una fondazione rigorosa della geometria doveva invece prendere le mosse da una concezione puramente aritmetica e metrica della varietà 3-dimensionale, con la quale l’idea relazionale di spazio della tradizione leibniziana, attraverso il continuo aritmetico, poteva essere quantificata. Era infatti già chiaro ai greci che la misura nel continuo, diversamente dal discreto, non è intrinseca, ed è quindi legata agli strumenti di misura, in generale connessi ai corpi rigidi e ai raggi di luce, e i cui comportamenti sono dettati dalle loro proprietà fisiche. La retta diventa allora la «curva di minima distanza», la geodetica, e quindi occorre partire dalla metrica: su una superficie infinitesima la metrica più ragionevole è una ovvia generalizzazione di quella usata da Gauss:

ma mentre in Gauss essa era derivata da quella pitagorica in R³, in Riemann essa è la più semplice compatibile con i caratteri alla base dell’idea di geometria. Una volta estratto da questa teoria delle varietà tutto ciò che se ne poteva dedurre a priori, la caratterizzazione finale dello spazio reale e degli enti geometrici doveva essere precisata empiricamente.

In particolare, se si voleva applicare questa geometria allo spazio reale, occorreva chiedere che ogni movimento del sistema di riferimento lasciasse invariati i corpi rigidi. Riemann comprese facilmente come questo fosse possibile solo in una geometria a curvatura costante (nulla nella geometria euclidea, positiva in quella ellittica, negativa in quella iperbolica), e la scelta tra queste doveva essere empirica.

Le geometrie non euclidee apparivano inaccettabili seguendo alla lettera Kant, che riteneva gli assiomi della geometria sintetici e derivabili dall’intuizione a priori. Ma già a Riemann questo sembrava un semplice pregiudizio. Si apriva così la questione su quale sia la vera geometria dello spazio reale. Molti (tra cui Hilbert) continuarono a credere che fosse quella euclidea la geometria dello spazio reale e quelle non euclidee solo possibilità matematiche. Vi fu chi ritenne la questione puramente empirica (lo stesso Riemann, Pasch, Helmholtz, Peano), chi considerò la scelta della geometria una pura convenzione e la scelta euclidea solo quella più comoda, il gruppo continuo euclideo essendo il più semplice e il moto dei corpi rigidi essendo psicologicamente evidente (Poincaré), e chi assunse la geometria proiettiva a forma generale del mondo esterno ritenendo empirica la scelta tra la geometria euclidea, ellittica o iperbolica (Russell). Infine Einstein collegò la geometria alla distribuzione di massa-energia nello spazio.

Emerse soprattutto l’esigenza di considerare ciò che nella descrizione del mondo esterno rimane invariante al variare del soggetto che conosce e che misura le grandezze, una esigenza che caratterizzerà la geometria moderna nel suo rapporto con le scienze fisiche. È in fondo l’antica urgenza che la scienza sia intersoggettiva, la stessa per tutti gli esseri razionali. Divengono così più importanti gli aspetti premetrici tipici della geometria proiettiva e dei suoi invarianti. Il principale di questi è il birapporto (cross ratio) tra 4 punti che sulla retta metrica è dato da AC × BD /AD × BC, invariante per proiezioni da un punto (ammessi anche punti all’infinito, come A″ in fig. 38, dove la quaterna A, B, C, D su s diventa A′, B′, C′, D′ su r e A″, B″, C″, D″ su t). Nella geometria proiettiva tutte le rette si incontrano, le parallele in un punto all’infinito sulla retta all’infinito (la linea d’orizzonte dei pittori rinascimentali), e la struttura della teoria appare molto più elegante.

La geometria proiettiva

Nella geometria proiettiva si inaugura anche un rapporto nuovo tra teoria matematica e linguaggio. L’aspetto linguistico della teoria non è più un riflesso naturale della naturale verità della geometria, ma deve garantire anche le esigenze di eleganza e semplicità della teoria. Le caratteristiche algebriche diventano sempre più importanti: nella geometria proiettiva della seconda metà dell’Ottocento si introducono i sistemi di coordinate omogenee. Così l’equazione di una curva nel piano (x, y) viene trasformata in un’equazione nel piano proiettivo (X, Y, Z) ponendo x = X /Z e y = Y /Z, la retta all’infinito ha equazione Z = 0, il fascio di rette con centro (X, Y, 0) rappresenta nel piano metrico un fascio di rette parallele: il punto di vista analitico rende finito e infinito omogenei.

Ugualmente tale rappresentazione analitica elimina le distinzioni non proiettive (tra punti esterni e interni a una conica, tra diversi tipi di coniche ecc.). Così Jean-Victor Poncelet (1788-1867), a cui dobbiamo la forma moderna della geometria proiettiva, generalizza il concetto di retta polare p a un punto P rispetto a una conica (in Apollonio la retta congiungente i punti di contatto delle tangenti da P) (fig. 39): la definizione aveva senso nel caso di P esterno alla conica, ma Poncelet la estende a punti R interni alla conica considerando immaginari i punti di contatto in una impostazione puramente analitica e algebrica; in tal caso la polare r diventa una retta senza punti di contatto reali con la conica. Un aspetto sorprendente di tale forma linguistica della geometria proiettiva è la scoperta del principio di dualità: data una proprietà vera della geometria piana proiettiva, è anche vera la sua proprietà duale, che si ottiene sostituendo il termine «punto» col termine «linea», «collineare» con «concorrente», e «giace su» con «passa per» e viceversa. Nella geometria spaziale lo stesso si ottiene scambiando il termine «punto» col termine «piano», lasciando invariato il termine «linea» e così via. Così, data una conica, spostandosi il punto P su una retta r le sue polari p sono un fascio di rette di centro R la cui polare è r. E il postulato «due punti distinti del piano determinano una e una sola retta» diventa «due rette distinte del piano determinano uno e un solo punto (al finito o all’infinito)». Qualcosa di analogo accade nella dualità tra variabili e parametri: la retta nel piano proiettivo aX + bY + cZ = 0 (a, b, c, fissati e X, Y, Z variabili) può anche essere letta dualmente come il fascio di rette passanti per il punto (X, Y, Z) fissato, al variare di a, b, c.

Geometria senza misura: la topologia

L’analisi rigorosa dei concetti fondamentali della geometria richiedeva che essi venissero isolati: questa è la ragione del proliferare di geometrie nell’Ottocento. L’idea di una geometria priva di qualsiasi connotazione metrica, quella che già in Leibniz era adombrata come analyis situs, si traduceva nella topologia. In essa si studiavano le proprietà geometriche (come la vicinanza o la connessione) invarianti per deformazioni che preservassero la sola continuità degli enti geometrici. Così è evidente che una deformazione continua può trasformare una ciambella col buco in un lucchetto chiuso, ma non in una sfera o in un lucchetto aperto (fig. 40).

Nel discreto essa si legava al concetto di grafo, apparso già nella soluzione di Eulero (1736) al problema dei ponti di Königsberg: il problema riguardava la possibilità di trovare un percorso per la città che passasse una e una sola volta attraverso tutti i ponti urbani, rappresentando i quartieri come vertici e i ponti come lati. Un altro problema topologico affrontato da Eulero riguardava il numero di facce ƒ, di lati s e di vertici v di un poliedro (anche nel grafo ottenuto proiettando il poliedro su un piano), e risultava la relazione ƒ + v − s = 2. Il carattere topologico del concetto di grafo emergeva dal fatto che per la risoluzione di questi problemi erano indifferenti dimensioni e forme di quartieri, ponti, facce, lati, mentre erano rilevanti solo le relazioni di incidenza tra vertici e lati.

La struttura topologica del continuo

Un altro filone dell’indagine topologica era la struttura topologica del continuo. L’idea intuitiva di intorno del punto p era quella di insieme di punti vicini a p (per esempio le sfere di centro p potevano essere gli intorni di p). Un punto p era interno a K se c’era un suo intorno contenuto in K, esterno se c’era un suo intorno disgiunto da K, limite se non era né interno né esterno, in altri termini se in ogni intorno di p c’erano punti di K e non di K. L’insieme dei punti limite era detto il bordo e un insieme senza punti limite era detto aperto, mentre il complemento di un insieme aperto era detto un insieme chiuso, che quindi conteneva i suoi punti limite.

Accentrando l’attenzione sugli aspetti non metrici, gli intorni diventavano generici insiemi aperti. Su queste basi si poteva poi sovrapporre una teoria della misura, basata sul riconoscimento di un insieme di aperti fondamentali dotati di una misura (per esempio gli intervalli aperti) e poi sulla definizione di misura esterna di un insieme, intesa come il limite inferiore della somma degli aperti fondamentali contenenti l’insieme.

Un altro concetto, già adombrato da Dirichlet, era quello dell’insieme K denso in un altro insieme S, quando in ogni intorno di un punto di S esisteva almeno un punto di K, e quindi ogni punto di S o apparteneva a K o ne era un punto limite: per esempio l’insieme dei razionali era un insieme denso nell’insieme dei reali.

L’«Erlanger Programm»

L’idea che lo studio di una proprietà geometrica di una figura potesse essere semplificata applicando alla figura una trasformazione (per esempio una proiezione poteva trasformare un’ellisse in un cerchio), che lasciasse invariata la proprietà stessa, aveva già fatto la sua apparizione nella storia della matematica. Col tempo risultò chiaro come le trasformazioni potessero interessare molti settori, inclusa la stessa risoluzione delle equazioni differenziali: le trasformazioni adattavano così la stessa intuizione geometrica a una geometria sempre più algebrica in cui certe strutture apparivano sempre più lontane dalla immaginazione spaziale tradizionale.

Felix Klein (1849-1925) nel 1872 fece la sua lezione inaugurale a Erlangen proprio facendo delle trasformazioni il punto centrale dello studio e classificazione delle geometrie, basandosi sulla relazione tra geometria, gruppo di trasformazioni e invarianti. Centrale era il concetto di varietà, inteso come uno spazio n-dimensionale, ottenuto su un calco euclideo in un certo senso liberato algebricamente dalle proprietà geometriche. Su di essa si poteva definire una trasformazione intesa come un’applicazione della varietà su sé stessa, per esempio una traslazione, una rotazione, una dilatazione. Inoltre la composizione (cioè l’applicazione successiva) di due trasformazioni doveva essere una trasformazione, la inversa di una trasformazione era una trasformazione, l’identità era una trasformazione e la composizione infine era associativa: le trasformazioni quindi costituivano un gruppo. Se un ente o proprietà geometrica era lasciato fisso dalle trasformazioni di un dato gruppo veniva detto un invariante per tale gruppo.

Klein a questo punto caratterizzava le diverse geometrie tramite i relativi invarianti e quindi i relativi gruppi di trasformazioni. Una stessa trasformazione su una varietà poteva essere considerata o come il risultato di un mutamento reale che modificasse le caratteristiche degli enti geometrici della varietà o come un cambiamento del sistema di riferimento in cui lo stesso ente geometrico assumeva nuove coordinate. L’esempio più ovvio era quello delle trasformazioni che lasciavano invariati i corpi rigidi e quindi i relativi angoli e lunghezze (le cosiddette isometrie): una tale trasformazione poteva essere vista come il risultato di una rototraslazione di un corpo o come la descrizione della sua posizione in un diverso sistema di riferimento ottenuto per rotazione e traslazione dell’osservatore. Un tale gruppo caratterizzava la geometria metrica.

Se si permettevano allungamenti per così dire elastici, il gruppo era quello delle trasformazioni affini (una trasformazione lineare più una traslazione) e si otteneva la geometria affine, in cui erano invarianti le rette e il loro parallelismo (ma non gli angoli né le distanze). Se si richiedeva solo che fossero invarianti le rette e i birapporti (ma non il parallelismo e i rapporti) si aveva il gruppo delle collineazioni e la geometria proiettiva, e in essa una metrica poteva essere introdotta tramite l’individuazione di una conica assoluta. La geometria proiettiva diventava così sempre più la geometria fondamentale, come diceva Cayley («la geometria proiettiva è tutta la geometria») e anche le geometrie non euclidee potevano essere caratterizzate a partire dalla geometria proiettiva.

L’idea di caratterizzare una geometria con il gruppo di trasformazioni che preservano gli invarianti tipici di quella geometria continuerà anche dopo Klein: per esempio gli spazi topologici verranno caratterizzati dagli omeomorfismi (che preservano la sola continuità) e Sophus Marius Lie (1842-99) studierà i gruppi continui di trasformazioni sullo spazio n-dimensionale.

La geometria diveniva la dottrina generale dello spazio e delle sue proprietà. E le proprietà stesse non erano più gli attributi di uno spazio già dato, ma caratterizzazioni analitiche autonome. Il “farsi e disfarsi” dello spazio diventava la ragion d’essere della geometria: probabilmente qualcosa che non sarebbe dispiaciuto a Kant.

L’algebra astratta

L’autonomia della sintassi portava lo stesso linguaggio matematico a diventare oggetto autonomo di studio. Esso era cresciuto a partire dal simbolismo algebrico cartesiano, estendendosi al linguaggio del calcolo e all’ars combinatoria di Leibniz. Era inoltre diventato progressivamente anche il linguaggio della fisica, trattando grandezze il cui senso era originariamente geometrico. L’algebra, che era stata la disciplina pratica per la risoluzione delle equazioni con metodi geometrici, diventava la tecnica della manipolazione simbolica delle quantità; e alla fine del Settecento, la ricerca delle risolventi per equazioni di grado superiore al quarto si indirizzava verso l’analisi algebrica del sistema delle radici, studiandone le funzioni simmetriche.

Gli enti algebrici come segni

Nell’Ottocento l’algebra comincia ad assumere la sua forma moderna, astratta: gli enti algebrici non sono più caratterizzati come numeri o grandezze, ma diventano semplicemente segni. La matematica cessa di essere la “scienza della quantità”. Nei secoli precedenti l’algebra aveva modificato profondamente la natura stessa dei segni: non più simboli passivi, ma oggetti manipolabili (sebbene astratti) il cui senso non era più dato dalle cose o dalle idee che esprimevano, ma dal loro uso nel calcolo; la sintassi non forniva più solo le regole per costruire espressioni corrette ma soprattutto le regole per tale manipolazione algebrica.

La possibilità di nuove interpretazioni rispetto al tradizionale senso geometrico e aritmetico è alla radice della distinzione tra sintassi e semantica, e della stessa questione semantica che si delinea nel xx secolo caratterizzando le teorie formali: quanto il significato di un segno sia intrinseco, fissato a priori, e quanto invece sia esterno, lasciato alla interpretazione dell’utente, tenendo presente che è il significato intrinseco a garantire tramite assiomi (regole, algoritmi, compilatori ecc.) la manipolazione automatica dei segni, il calcolo.

Nell’Ottocento gli assiomi sono ricavati dal significato tradizionale dei concetti e ne caratterizzano il trattamento sintattico. Per esempio in una concezione aritmogeometrica la proprietà commutativa del prodotto non ha rilievo, poiché esprime solo l’invarianza dell’area di un rettangolo per una rotazione di 90°; essa acquista risalto solo quando (alla fine del Settecento) prevale il linguaggio algebrico, e progressivamente alcuni simboli si svuotano del loro senso tradizionale e cominciano a essere caratterizzati solo formalmente: così in Dedekind i simboli hanno il senso aritmetico tradizionale, ma si richiede che siano gli assiomi introdotti a caratterizzare completamente il loro comportamento.

All’inizio dell’Ottocento l’assiomatizzazione è una realizzazione sintattica che, se non resta semplice calcolo, non perde mai del tutto di vista il suo referente semantico, rimane cioè sempre legata al suo modello standard, sia che si tratti di una struttura numerica, oppure di un insieme di trasformazioni o permutazioni, o ancora di un sistema di grandezze fisiche. Solo verso la fine del secolo giunge a compimento il processo di astrazione definitiva dal significato tradizionale dei segni, con la netta contrapposizione tra sintassi e semantica e la distinzione rigida tra primitive (definite implicitamente dagli assiomi) e termini vuoti privi di significato sintattico, la cui caratterizzazione è totalmente devoluta all’interpretazione soggettiva, così che la stessa struttura algebrica può essere interpretata nelle discipline più diverse.

La caratterizzazione solo sintattica delle proprietà degli enti porta a un altro concetto fondamentale: quello di isomorfismo; esso estende l’idea di corrispondenza biunivoca richiedendo che essa preservi relazioni e funzioni. Diventando sempre più esplicito il carattere sostanzialmente non interpretato dei simboli non primitivi, il concetto di isomorfismo costituirà l’idea stessa di identità tra strutture algebriche: dire che due strutture sono isomorfe equivale a dire che si tratta della stessa struttura.

Il gruppo

La più basilare di tali strutture è quella di gruppo, introdotta negli anni Trenta del xix secolo da Évariste Galois (1811-32) per dimostrare la insolubilità tramite radicali delle equazioni di grado superiore al quarto. Il gruppo è caratterizzato da un’operazione binaria associativa dotata di elemento neutro e di inversa (per esempio Z con la somma come operazione, il negativo come inversa e lo 0 come elemento neutro, ma se si aggiunge il prodotto Z diventa una struttura più complessa, un anello).

La ricchezza del mondo delle strutture algebriche appare soprattutto nell’opera di Dedekind, che introduce gli ideali e l’idea di applicazione tra insiemi, considera strutture dotate anche di relazioni (di equivalenza, con relative classi di equivalenza, e di ordine, come i reticoli) e studia i corpi commutativi (campi) con i quali caratterizza insiemi numerici quali i razionali, i reali, i complessi.

Di natura algebrica è anche la teoria intrinseca delle grandezze di Hermann Grassmann (1809-77), nella quale queste non vengono viste più come enti riducibili ai numeri reali, ma in sé stesse come dotate di una certa struttura algebrica (l’esempio più noto è quello dei vettori). Analoghe la teoria dei quaternioni di William Rowan Hamilton (1805-65) e la teoria delle matrici; quest’ultima sarà la base della futura algebra lineare e diventerà uno degli strumenti matematici principali della fisica moderna.

La nascita dell’algebra astratta segna un mutamento radicale del ruolo del segno. Mentre nel calcolo settecentesco esso aveva solo la funzione di “ingrediente” degli algoritmi, privo di significato se non nelle applicazioni fisiche, nell’algebra astratta esso appare invece definito dal sistema di assiomi che caratterizza la struttura algebrica.

La logica di Boole

La logica nel Settecento era diventata una disciplina marginale che sopravviveva solo nelle università. Era comune e condivisa l’opinione kantiana che si trattasse di una disciplina ormai ovvia e immodificabile, in genere considerata quasi inutile per la scienza. Ma già verso la metà dell’Ottocento, soprattutto in Inghilterra, la logica di George Boole (1815-64) mette in luce una nuova connessione tra l’algebra e la logica, in cui quest’ultima appare come applicazione dell’algebra alle leggi del pensiero. La logica di Boole è una logica delle classi, capace di esprimere i costrutti fondamentali della logica aristotelica, sulla linea di una lettura estensionale della logica già iniziata da Eulero e ripresa da John Venn (1834-23) (fig. 29), e nella quale si delinea anche l’omogeneità (già accennata in Bolzano) con il ragionamento probabilistico.

La logica di Boole è in realtà un aspetto della svolta che la matematica inglese vive sin dall’inizio del xix secolo grazie al lavoro della Analytical Society, nata per adeguare l’analisi di tradizione newtoniana al formalismo leibniziano. Questa associazione ha dato all’algebra inglese (e a tutta la matematica inglese) un’impronta particolare, segnata dall’attenzione verso l’analisi formale delle operazioni e il calcolo, con le sue diverse interpretazioni e la sua automazione: uno dei fondatori dell’associazione era infatti Charles Babbage (1791-1871), creatore della macchina analitica, primo esempio di calcolatore con programma incorporato.

In Germania tra algebra e logica si profila invece una connessione più radicale: i concetti di intensione ed estensione trovano la loro realizzazione più chiara nel rapporto tra proprietà e classi, mentre la relazione tra sintassi e semantica si ritroverà nella correlazione tra la teoria assiomatizzata e le strutture algebriche: per esempio, la teoria dei gruppi è una teoria assiomatizzata di cui i diversi gruppi sono tutti e soli i modelli.

L’infinito, la logica e la teoria ingenua degli insiemi

Ancora in Gauss l’idea di infinito apparteneva alla penombra della matematica, ma la seconda metà dell’Ottocento si caratterizza anche per la crescente pratica del transfinito, con il quale assume un ruolo sempre più centrale il concetto di insieme basato sul principio analitico che “il tutto è la somma delle sue parti”, un concetto fino al Seicento più assurdo che inutile in una matematica (e in una filosofia) dominate dal concetto olistico di “sostanza”. La connessione tra le idee di insieme e di infinito nasceva da un fenomeno tipico della matematica: il trasformarsi in cosa di un segno. Infatti le molteplicità infinite, quando menzionate per esempio in una dimostrazione, non potevano essere descritte elencandone gli elementi, andavano “riassunte” in un segno, e di esse si dovevano poi considerare i singoli elementi, le relazioni con altri insiemi ecc. Nasceva così, prima dell’insieme, una sintassi insiemistica.

L’accettazione piena dell’infinito in matematica inizia già con Bolzano e si sviluppa nel corso del secolo (i limiti in analisi, i punti all’infinito nella geometria proiettiva, i numeri reali ecc.); in Dedekind è normale l’uso di insiemi attualmente infiniti (i numeri interi, razionali, reali) e di funzioni tra di essi. Ma la teoria trova la sua consacrazione ufficiale nel transfinito di Cantor, in cui l’insieme è il risultato di una riunione (denotata con un simbolo) di oggetti determinati e distinti (gli elementi), intuiti o pensati, e la sua cardinalità il risultato di una doppia astrazione dalla natura e dall’ordine dei suoi elementi.

L’insieme transfinito di Cantor

Cercando di caratterizzare il rapporto tra una funzione e la sua serie di Fourier (in particolare l’unicità di quest’ultima), l’analisi aveva studiato funzioni con un numero di discontinuità o di punti estremali anche infinito. Cantor aveva ottenuto sul problema della unicità risultati importanti, dimostrandola anche per funzioni in cui fossero presenti insiemi infiniti di punti eccezionali, ma si poneva il problema di immergerli nel continuo, e quindi si ripresentava il problema del confronto tra insiemi infiniti. Cantor lo affrontava assumendo il principio aritmetico per il quale «due insiemi in corrispondenza biunivoca hanno la stessa cardinalità» e rigettando quello geometrico secondo cui «il tutto è maggiore della parte», la cui inapplicabilità in insiemi infiniti, con Dedekind, era alla base della definizione stessa di insieme transfinito: un insieme che si può mettere in corrispondenza biunivoca con una sua parte propria.

Questa analisi riguardava all’inizio gli insiemi di punti, ma presto Cantor la generalizzò a insiemi qualsiasi, studiando in primo luogo gli insiemi numerabili, quelli che si possono mettere in corrispondenza biunivoca con il più piccolo insieme infinito N e ne hanno quindi la stessa cardinalità |N|. Sorprendentemente trovava insiemi numerabili anche molto grandi, quali l’insieme dei numeri razionali, l’insieme dei numeri algebrici, l’insieme N* formato da tutte le sequenze finite di numeri interi, e in generale ogni insieme Σ* formato da tutte le sequenze finite di caratteri di un alfabeto numerabile Σ. Risultano così numerabili l’insieme di tutte le espressioni algebriche, l’insieme di tutte le formule del calcolo dei predicati, l’insieme di tutti i programmi in C++ ecc. Un aspetto cruciale di queste corrispondenze era che erano effettive, algoritmiche, si trattava cioè di autentiche codifiche e decodifiche. In generale si poteva codificare in N qualunque insieme i cui elementi fossero comunque finitamente esprimibili in qualsivoglia alfabeto. Tenendo presente che ogni numero intero si può poi codificare binariamente, come elemento cioè di {0, 1}*, si è qui in presenza di uno dei fatti matematici su cui si basa il computer moderno, cioè la capacità di rappresentare al suo interno qualsiasi insieme di dati comunque esprimibili e realizzare così una characteristica universalis.

Successivamente Cantor tramite l’argomento diagonale dimostrava che anche il più piccolo intervallo di R ha una cardinalità superiore a quella di N. Questi risultati mostravano da un lato la completa rappresentabilità sintattica del discreto, dall’altro la completa non rappresentabilità sintattica del continuo. Cantor riusciva sorprendentemente anche a dimostrare l’equicardinalità di R con R^p, per p intero: per esempio a ogni coppia (0, r₁ r₂ r₃ ...; 0, s₁ s₂ s₃ ...) di numeri reali in [0, 1[² si può far corrispondere biunivocamente un numero 0, r₁ s₁ r₂ s₂ r₃ s₃ ... in [0, 1[ (con qualche cautela per i numeri periodici). È tuttavia evidente che questa corrispondenza non preserva la continuità, e che in tal modo la dimensionalità di un continuo non è un invariante per corrispondenze discontinue e ha quindi un carattere topologico.

Occorre notare come la prima dimostrazione della non numerabilità del continuo fosse stata abbastanza complessa e basata su un’analisi della topologia degli insiemi continui di punti. L’argomento diagonale si rivelava invece molto più semplice e generale: la non numerabilità del continuo in realtà diventava un caso particolare di un teorema generale, quello secondo cui per ogni insieme M detto ℘(M) il suo insieme delle parti, |M| < |℘(M)|.

La dimostrazione è in fondo molto semplice: essendo M equipotente a una parte di ℘(M), la sua cardinalità è minore o uguale a quella di ℘(M). Per escludere che possano essere uguali, si supponga per assurdo l’esistenza di una corrispondenza biunivoca ƒ: M → ℘(M), e si consideri l’insieme H = {x ∈ M | x ∉ ƒ(x)}. Essendo H ∈ ℘(M) esisterà un h ∈ M tale che ƒ(h) = H, e possiamo chiederci se h ∈ H. In tal caso h ∉ ƒ(h) e quindi h ∉ H. Viceversa se h ∉ H si deduce che h ∈ H. La non numerabilità del continuo (cioè di qualsiasi intervallo di R) ne consegue quando si osservi che si può mettere in corrispondenza biunivoca ogni intervallo di R con ℘(ℵ). L’argomento diagonale ricalca paradossi come quello del mentitore e sarà il modello per molte dimostrazioni cruciali della metamatematica.

Si poteva allora generare una sequenza di cardinali transfiniti di origine numerica:

Passando poi agli ordinali transfiniti Cantor studiava i modi non isomorfi con cui insiemi con la stessa cardinalità transfinita potevano essere ben ordinati (ordinati in modo tale che ogni sottoinsieme limitato inferiormente ammettesse un minimo). Considerando ω l’ordinamento naturale di N, l’aggiunta di un nuovo elemento prima dello zero creava un ordinamento isomorfo a ω, e quindi 1 + ω = ω, ma se l’elemento nuovo era aggiunto dopo tutti i naturali si otteneva un ordinamento non isomorfo (sebbene equipotente con N), ω + 1 ≠ ω. Si potevano allora costruire tutti gli ordinamenti transfiniti di cardinalita |N| = ℵ₀ (che si legge «aleph zero»), utilizzando una procedura puramente combinatoria consistente di due principi generativi: il primo aggiungeva 1, il secondo costruiva il limite di una sequenza senza un massimo: per esempio ω era il massimo della sequenza di tutti i numeri naturali, 2ω il massimo della sequenza di tutti gli ω + n con n numero naturale. Si poteva continuare questo processo con l’unico principio limitativo di consentire solo sequenze (a partire da 1) di cardinalità ℵ₀. La cardinalità di questo insieme di ordinali, generato combinatorialmente e coincidente con la cardinalità dell’insieme di tutti i buoni ordinamenti distinti di insiemi numerabili, era un transfinito maggiore di ℵ₀ e non esistevano transfiniti di cardinalita intermedia: era naturale denotare tale transfinito con ℵ₁. Si delineava una nuova gerarchia di cardinali generabili per via puramente combinatoria, la gerarchia degli aleph, che includeva tutti i cardinali transfiniti

Si poneva allora il problema: le due gerarchie, quella basata sugli insiemi numerici e quella impostata sugli ordinamenti e sulla generazione sintattica, coincidono? In particolare |R| (= |℘(N)|) = ℵ₁? La risposta positiva è la cosiddetta ipotesi del continuo, che si può anche formulare come la congettura che ogni sottoinsieme di R debba avere la cardinalità di R o quella di N. Questa ipotesi era anche connessa al principio del buon ordinamento, secondo il quale ogni insieme era ben ordinabile; si poteva quindi ben ordinare l’insieme dei cardinali, restando aperto solo il problema della collocazione di R in tale ordine. Era tuttavia un principio difficile da accertare: l’insieme dei numeri reali nel loro ordine naturale non è ben ordinato (non esiste per esempio il minimo reale positivo) e nessuno sa come si potrebbe ben ordinare.

Quando nel 1900 Hilbert formulerà al Congresso mondiale dei matematici i suoi famosi 23 problemi matematici che il nuovo secolo doveva affrontare, l’ipotesi del continuo sarà il primo problema, e rimane a tutt’oggi uno dei massimi problemi fondazionali ancora aperti. L’ipotesi del continuo poteva essere generalizzata richiedendo che, per ogni i, |℘(ℵ_i)| = ℵ_i+1.

La teoria di Cantor, introducendo la possibilità di un confronto rigoroso tra i transfiniti, doveva avere un’influenza cruciale su tutta la matematica, aprendo la strada a una teoria della misura in grado di affrontare i complessi fenomeni che si andavano manifestando nell’analisi delle funzioni. Si poteva allora parlare di insiemi di misura nulla diversi dall’insieme vuoto (quali un insieme numerabile di punti su una retta) o di proprietà vere in un intervallo «quasi ovunque» (ovunque eccetto in un insieme di punti di misura nulla).

Il logicismo

Parallela alla nascita della teoria degli insiemi è l’elaborazione della logica matematica di Friedrich Ludwig Gottlob Frege (1848-1925).

Già Bolzano aveva abbandonato l’idea che la logica fosse una teoria psicologica delle idee e dei giudizi mentali o un arte del pensare, per considerarla invece una dottrina della scienza concernente le relazioni formali tra le proposizioni intese come enti oggettivi. Ma sopravviveva in lui l’antica concezione sostanzialistica del mondo, fatto di sostanze (individuali o universali) portatrici di attributi e relazioni (intese come attributi esterni). Frege supera tale concezione considerando la proposizione non più formata da un soggetto e un attributo, bensì da una relazione intesa come funzione con n termini come argomenti. Sottolinea anche che il significato dei termini vada compreso nel contesto della proposizione, ma questo non per un’esigenza olistica, quanto piuttosto per la necessità di caratterizzare una definizione tramite relazioni. Era questa un’istanza della matematica ottocentesca in cui si moltiplicavano gli enti (come i punti all’infinito) non caratterizzati da attributi ma definibili solo tramite relazioni.

Frege introduce una “scrittura” molto particolare (la Begriffschrift, “scrittura dei concetti”: in fig. 41 a sinistra l’equivalente di Δ ⇒ Γ, al centro l’equivalente di ¬Γ, a destra l’equivalente di ∀aΓ), oggi desueta perché sostituita dalla notazione più algebrica introdotta da Giuseppe Peano (1858-1932).

La scrittura fregeana appare più iconica, ma la sintassi ha un carattere composizionale: ogni tratto dei simboli ha un significato primitivo e il significato complessivo si ottiene dalla giustapposizione dei significati elementari. E inoltre, come nell’algebra astratta, anche nella logica fregeana si distinguono costanti, variabili (viste come argomenti “vuoti” di funzioni o predicati), predicati e funzioni. A essi si aggiungono connettivi e quantificatori, e sono questi ultimi una della novità più rilevanti. Nonostante la notazione di Frege sia facilmente traducibile nel linguaggio logico moderno, essa non appare come una sintassi scissa dalla semantica, ma come pura espressione delle leggi del pensiero.

Altra novità è che la dimostrazione assume una caratterizzazione puramente sintattica, come sequenza finita di formule ciascuna delle quali o è un assioma o si può ricavare dalle formule precedenti tramite regole di inferenza, così che la verifica della correttezza di una dimostrazione può essere fatta meccanicamente. D’altra parte Frege vuole creare una scrittura con cui soprattutto rendere trasparente e rigoroso il ragionamento matematico, fino a ridurre l’aritmetica a “logica travestita”. E come quella di Frege è una logica “oggettiva”, senza valenze psicologiche, tale è anche l’aritmetica, che non ha nulla di empirico o di meccanico: il numero naturale associato a un concetto è un oggetto ottenuto come estensione del concetto di equinumerosità (esistenza di una corrispondenza biunivoca tra le estensioni dei concetti) rispetto a tale concetto, e i giudizi aritmetici sono analitici. La concezione di Frege viene detta logicismo, e rappresenta il primo tentativo di dare una risposta al problema dei fondamenti della matematica.

Iniziava così un processo di sovrapposizione tra due discipline che per millenni erano state distinte, anzi quasi poli opposti (teorico e pratico) della scienza: il pensiero logico e quello algoritmico, la cui fusione segnerà la nascita della computer science.

Essenziale era la connessione tra teoria degli insiemi e logica matematica. Oggi essa ci appare come corrispondenza tra semantica e sintassi, la seconda costruita come manipolazione secondo regole di simboli e la prima come interpretazione insiemistica di questa. Esse nascono nell’Ottocento come praticamente sovrapponibili (anche se in forme diverse da Bolzano a Boole e a Frege, e con diverse preferenze: Boole appariva più estensionale, Frege più intensionale), connesse all’isomorfismo tra la intensione p (il concetto) visto come predicato, e la sua estensione P (l’insieme degli oggetti a cui il concetto si applica), definibile tramite le relazioni:

Frege in realtà coglieva la distinzione tra intensione ed estensione in termini di senso e significato, citando l’esempio di Venere conosciuta dagli antichi sia come stella della sera (Vespero, quando tramonta subito dopo il sole) che come stella del mattino (Lucifero, quando sorge subito prima del sole), così che i due termini distinti rivelavano due sensi diversi per lo stesso referente, il pianeta Venere.

La caratterizzazione simbolica favoriva la distinzione tra sintassi e semantica, netta ma non tematizzata in Boole dove il formalismo assume l’aspetto di un calcolo, ed esplicita in Frege, dove però si ha una sovrapposizione in cui i simboli appaiono il linguaggio naturale del pensiero.

Oggi chiamiamo questa teoria la teoria ingenua degli insiemi; ingenua poiché esposta a innumerevoli antinomie, tra le quali il celebre paradosso dovuto a Bertrand Russell (1872-1970), relativo all’insieme R = {x|x ∉ x}: si vede subito dalle relazioni precedenti che R ∉ R ⇔R ∈ R. Russell era un seguace di Frege, ma si rese conto che nella logica fregeana si poteva costruire tale antinomia e glielo comunicò, causando di fatto la crisi del primo logicismo e della teoria ingenua degli insiemi. Russell proporrà un nuovo logicismo fondato sull’idea di una matematica come dottrina delle proposizioni condizionali, e nei Principia Mathematica, scritti con Whitehead, fornirà una traduzione logicista della matematica elementare.

Per costruire la matematica Dedekind, Cantor e Frege avevano cercato di sottolinearne il presupposto logico e formale. Si trattava di un approccio ancora ottocentesco, interno a una fondazione razionale e concettuale della matematica. Ma il crescere delle tendenze formaliste alla fine dell’Ottocento delineava un’opposizione al logicismo: la frattura definitiva fra un approccio logicista e uno formalista si realizzerà con una nuova ars combinatoria, quella di Hilbert.

La matematica nel xx secolo

I processi cognitivi che plasmano la matematica del xx secolo sono in parte l’eredità del secolo precedente:

1) la crisi del fondamento sia empirico sia razionalista della matematica, e la ricostruzione logico-formale dei suoi concetti;

2) la distinzione tra sintassi e semantica, l’autonomia e la centralità del sintattico.

La nascita della logica matematica aveva posto fine alla concezione sostanzialistica del mondo, che dopo Frege veniva descritto in termini di individui considerati come argomenti di predicati, entrambi inscritti in una forma logica come segni il cui significato era dato da un’interpretazione esterna, incastonati in un sistema di “primitive” il cui significato era invece dato a priori dalla sintassi.

La teoria era ormai l’unica forma di accesso scientifico alla realtà, includendone tanto gli aspetti deduttivi quanto l’utilizzazione empirica.

Si delineano anche processi nuovi che caratterizzano tutta la cultura del xx secolo:

1) la fine della centralità della mente come luogo delle idee, incluse le idee e i costrutti mentali nella scienza;

2) la riduzione della matematica a strumento solo sintattico della scienza.

L’“oblio della mente” è un processo che si diffonde in tutte le sfere della cultura ai primi del secolo. Appare all’inizio come fenomenologia o rifiuto positivista della metafisica e dei modelli mentali nelle scienze fisiche, in cui gli enti reali diventano solo osservabili e misurabili, come comportamentismo in psicologia, come strutturalismo in linguistica, come empirismo e pragmatismo in filosofia della scienza. In matematica esso implica che i simboli sono vuoti di significato, il quale viene loro assegnato soltanto o tramite assiomi o, nelle applicazioni, tramite l’interpretazione: nel Novecento è impensabile definire gli elementi degli insiemi oggetti del pensiero, o dimostrare l’esistenza di un insieme infinito usando un insieme di pensieri, come facevano Dedekind e Bolzano.

È la crisi del razionalismo a base matematica che sin da Galileo aveva sovrainteso allo sviluppo della scienza, sostituito da orientamenti diversi:

• una “svolta linguistica”, che sottolinea gli aspetti linguistici e convenzionali della matematica, strumentale alla scienza empirica: caratterizza non solo il convenzionalismo di Poincaré, il formalismo e il positivismo logico, ma anche tutto il logicismo dopo Frege e la filosofia analitica;

• l’esigenza di una fondazione a priori in una intenzionalità o in un’intuizione prerazionali: contraddistingue gli intuizionisti ma anche Husserl;

• tendenze platoniste, da Frege a Gödel, che si fondano sul presupposto di una esistenza oggettiva e autonoma degli enti logico-matematici o comunque sulla decidibilità di tutti i suoi asserti, come base della certezza della matematica, a prescindere dalla sua connessione con la realtà concreta.

La disciplina in cui questa svolta ha lasciato il segno più chiaro è la computer science: in essa la mente viene ridotta a un linguaggio, di tipo più o meno logico, o a un effetto della struttura neuronale connessionista del cervello.

I paradossi

Il passaggio fra i due secoli vide il fiorire dei paradossi: quello di Russell non era l’unico. Anche Cantor aveva scoperto nella sua teoria un’antinomia: quella dell’insieme di tutti gli insiemi, U. Per il teorema sull’insieme delle parti: |U| < |℘(U)|, ma ℘(U) era un insieme di insiemi e quindi un sottoinsieme di U, da cui |U| ≥ |℘(U)|.

Altri paradossi chiamavano in causa il concetto di “definizione”, come il paradosso di Berry, che considera «il più piccolo intero non definibile con meno di ventisei sillabe», ma che nel momento stesso in cui viene enunciato viene definito con meno di ventisei sillabe. L’affermarsi della concezione estensionale della logica tende a considerare questi ultimi paradossi solo semantici e tema di riflessione linguistico-filosofica, a differenza dei primi, ritenuti insiemistici e oggetto proprio della fondazione logica e in particolare della assiomatizzazione della teoria degli insiemi.

I paradossi erano però solo la punta dell’iceberg: il vero problema era il distacco totale maturato nell’Ottocento della matematica da ogni fondamento empirista o razionalista. Non era più la dimostrazione euclidea il paradigma della razionalità e la matematica non coincideva più con la descrizione fisica del mondo. Si era affermata pienamente la libera creatività dello spirito umano già delineatasi nell’Ottocento che, una volta rigettato il ruolo autonomo della mente, si riduceva ormai nel Novecento alla semplice scelta di un opportuno sistema di simboli. Certo la fisica restava una fonte essenziale di problemi e il rigore dimostrativo appariva sempre più necessario, ma non bastava: occorreva fondare la creatività matematica su un a priori sintattico. Già la fine dell’Ottocento aveva dato una prima risposta con il logicismo di Frege, ma in esso ancora appariva centrale il ruolo della mente, che già nel logicismo di Russell diventa del tutto superflua.

L’assiomatizzazione e il formalismo

La separazione tra sintassi e semantica aveva dapprima motivato l’idea che la geometria “reale” fosse una sorta di scienza naturale basata sul comportamento dei corpi rigidi, e questo nell’Ottocento aveva favorito una concezione convenzionalista o empirista; nel Novecento, invece, suggerisce piuttosto una strutturazione puramente assiomatica del suo linguaggio, suscettibile di interpretazione. Questo passaggio si compie in Moritz Pasch (1843- 1930) negli ultimi decenni del secolo. In Pasch si trova un embrionale formalismo e una prima forma di assiomatizzazione di una geometria in cui le definizioni dei concetti di base scompaiono perché appaiono ovvie sulla base dell’esperienza empirica, e gli assiomi traducono le relazioni concettuali universalmente accettate.

Dedekind

Anche le assiomatizzazioni proposte da Dedekind del concetto di continuo e dell’aritmetica possono essere inquadrate in questa prima versione del formalismo. In Essenza e significato dei numeri (1888) il rapporto tra il sistema di assiomi (sintassi) e i suoi possibili modelli (semantica) viene esposto in una forma quasi attuale. Ma mentre oggi le teorie matematiche muovono dagli assiomi e ne studiamo i modelli, Dedekind invece “estrae” gli assiomi dall’aritmetica “data”. Questa assiomatizzazione dell’aritmetica è emblematica, in quanto l’aritmetica, diversamente dalla geometria, non era mai stata veramente assiomatizzata. Alla fine del xix secolo Dedekind e poi Peano ne forniscono l’assiomatizzazione che ancora oggi noi usiamo: il punto di partenza di tale assiomatizzazione può essere trovato nell’idea di insieme infinito come insieme che si può mettere in corrispondenza biunivoca con una sua parte propria e nella proprietà dell’induzione completa. Si può sostenere che questa prima versione del formalismo si basa sulla traduzione sintattica di concetti e proprietà già acquisiti e condivide l’esigenza logicista di ricostruire logicamente i concetti matematici.

L’assiomatizzazione di Dedekind non è assimilabile al formalismo hilbertiano, in quanto per esempio per Dedekind i numeri reali non sono tout court le sezioni, ma esistono autonomamente nella mente creatrice e le sezioni dei razionali ne disvelano solo la struttura logico-insiemistica; anche la dimostrazione in Dedekind appare necessaria non solo per garantire la verità, ma anche per evidenziare tale struttura. Non è nemmeno riconducibile al logicismo, per la stessa ragione: i numeri reali sono una creazione dello spirito umano e non un travestimento di un’idea logica; l’insiemistica di Dedekind non ha nulla di filosofico, ma affonda le sue radici nel trattamento matematico dell’infinito: Frege analizza il concetto di numero, Dedekind la teoria dei numeri. Ma già vi si riconoscono aspetti (in temi quali la categoricità dell’assiomatizzazione, la definizione tramite assiomi, l’indipendenza e la completezza del sistema di assiomi) del formalismo hilbertiano, quando le radici concettuali e la caratterizzazione genetica della formalizzazione svaniranno dall’orizzonte fondazionale.

Hilbert

La versione più influente del formalismo si deve a David Hilbert (1862-1943). Con Hilbert il carattere formale della matematica diventa direttamente costitutivo della intera razionalità: la scienza emerge da una conoscenza intuitiva, ma nella sua forma teoretica non richiede altro che la manipolazione (sintattica e finitaria) dei segni da un lato e l’interpretazione semantica delle teorie formali dall’altro. In un certo senso è il coronamento dell’idea ottocentesca che gli assiomi dovessero “esplicitare” le proprietà dei concetti nel momento in cui tale esplicitazione è così esauriente da caratterizzare completamente il concetto e in tal modo svuotarne la definizione. In tale sistema, la semantica si caratterizza allora come l’insieme dei modelli del sistema di assiomi: se il sistema è categorico (ammette un solo modello a meno di isomorfismi) il significato del segno è univocamente determinato e la sintassi, come una sorta di dna, “cattura” il senso della teoria da assiomatizzare.

In Hilbert i concetti fondamentali della geometria (punti, linee ecc.) non richiedono definizioni, le quali hanno solo la funzione secondaria di denominare sinteticamente lunghe espressioni di concetti derivati. Scriveva nel 1899 a Frege: «Ogni teoria è solo una impalcatura o uno schema di concetti insieme con le loro mutue relazioni, e gli elementi di base possono essere concepiti in qualsiasi modo si desideri. Se prendo come “punti” un qualsiasi sistema di cose, per esempio quello formato da amore, legge, spazzacamino… e considero tutti i miei assiomi come relazioni sussistenti tra di essi, allora i miei teoremi – per esempio il teorema di Pitagora – varranno anche per tale sistema di cose».

Nella sua assiomatica della geometria gli assiomi sono organizzati in gruppi nei quali alcuni concetti, a partire da quello di punto, ricevono una caratterizzazione implicita (e categorica): il primo gruppo caratterizza la incidenza e definisce implicitamente anche la linea e il piano; il secondo gruppo caratterizza l’ordine definendo la relazione “stare fra due punti”; il terzo gruppo caratterizza la congruenza, cioè la equidistanza tra punti. Un quarto gruppo è l’assioma delle parallele che con gli altri tre caratterizza la geometria euclidea. Gli ultimi due assiomi introducono il concetto di continuità, e sono l’assioma di Eudosso-Archimede («Dati due segmenti esiste un multiplo del minore che sia maggiore del maggiore») e l’assioma di completezza, il quale non è però un assioma in senso stretto perché coinvolge gli altri assiomi e i loro modelli: «È impossibile aggiungere altri elementi (punti, linee, piani) senza violare qualche assioma», cioè il modello della teoria è unico in quanto non estendibile o, equivalentemente, è il massimo dei modelli possibili. Tanto questo assioma quanto la dimostrazione di categoricità della assiomatizzazione dell’aritmetica si basavano sulla mancanza di una distinzione rigida tra logica del primo ordine (in cui è consentita solo la quantificazione degli individui) e la logica del secondo ordine (in cui è consentita anche la quantificazione di predicati e funzioni), e tra sintassi e semantica. Tanto la indipendenza quanto la consistenza degli assiomi erano dimostrate con la costruzione di modelli (per la consistenza il modello era la teoria dei numeri reali e quindi la consistenza della geometria era semplicemente ridotta alla consistenza dei reali).

Hilbert sottolinea la differenza tra una fondazione genetica e una assiomatica: se si considera per esempio il sistema dei numeri reali, geneticamente esso veniva caratterizzato dalle definizioni di Cantor o Dedekind che lo costruivano a partire dai numeri razionali, assiomaticamente esso è un campo totalmente ordinato e completo. La distanza concettuale è notevole, ma è anche vero che le due caratterizzazioni sono equivalenti.

La fertilità dell’approccio formalista si sarebbe rivelata nei primi decenni del secolo non solo nella assiomatizzazione di altre teorie matematiche, come la teoria degli insiemi, ma anche nella creazione di strutture matematiche del tutto nuove, come gli spazi di Hilbert, che generalizzavano a infinite dimensioni l’idea tradizionale di spazio geometrico, diventando tra l’altro il linguaggio matematico di base della meccanica quantistica.

La matematica finitista di Hilbert

Hilbert riconosceva che l’uomo è un essere finito incapace di trattare immediatamente l’infinito e che quindi tutta la matematica dovesse essere fondata su tecniche finitiste, ma voleva salvare il paradiso del transfinito cantoriano tramite l’uso della dimostrazione formale, che permetteva al matematico di conoscere proprietà di insiemi infiniti con una tecnica finitista in quanto la stessa dimostrazione è un oggetto finito (così per esempio tramite il principio di induzione completa si possono scoprire proprietà dell’insieme infinito dei numeri naturali). Esistevano quindi due matematiche: una reale, contenutistica, che includeva l’aritmetica e la geometria elementari cui l’uomo aveva un accesso diretto, e una ideale, solo formale, che l’uomo poteva conoscere solo per via indiretta, dimostrativa. Nella matematica reale la via dimostrativa doveva portare agli stessi risultati. Un classico esempio era costituito dai punti della geometria: quelli reali della geometria euclidea e quelli all’infinito della geometria proiettiva, concepibili solo per via dimostrativa.

Hilbert era un estimatore della logica di Frege, del quale condivideva l’idea di una stretta connessione tra logica e aritmetica, ma riteneva che il fondamento a priori della matematica fosse non la logica ma una capacità umana puramente sintattica, quella di ragionare manipolando segni, gli unici oggetti mentali su cui si poteva fondare la matematica, la scienza e l’intelligenza umana. Era il punto di approdo di tutta la tradizione filosofico-scientifica tedesca: l’a priori kantiano e la struttura sintattica della conoscenza leibniziana, l’infinito cantoriano e la logica fregeana. I significati dei segni, i concetti coinvolti negli assiomi, erano dati in forma implicita dal sistema di assiomi: in maniera univoca se tale sistema era categorico oppure, in caso contrario, lasciati alla scelta dell’interprete. Per Hilbert la matematica pura si fondava su assiomatizzazioni categoriche; era questa l’unica base per comprendere tali concetti: per esempio il concetto di continuo era comprensibile solo attraverso una sua assiomatizzazione categorica.

Verità e dimostrazione in Hilbert e Frege

Questa riduzione sintattica della matematica richiedeva che l’idea stessa di verità fosse ricondotta a quella di dimostrazione, il principio di non contraddizione si riduceva allora alla richiesta della consistenza della assiomatizzazione (che garantiva l’esistenza di un modello e per Hilbert l’esistenza degli stessi enti matematici coinvolti), e il principio del terzo escluso (tertium non datur) si traduceva nella completezza sintattica (per ogni formula A doveva essere dimostrabile A oppure dimostrabile non A).

Era cruciale verificare che i concetti di dimostrazione e di verità fossero sovrapponibili così che i teoremi coincidessero con le verità matematiche (correttezza e completezza semantica): un passo decisivo in questa direzione fu fatto da Kurt Gödel (1906-78), che nel 1929 dimostrò che il calcolo dei predicati del primo ordine era semanticamente completo.

Già l’iniziale delinearsi dell’idea formalista aveva incontrato l’opposizione di Frege, e la polemica epistolare con Hilbert è emblematica del passaggio dalla matematica del xix secolo a quella del xx. Il contrasto infatti verteva soprattutto sul ruolo rispettivo dei concetti e dei segni. Per Frege erano i primi con le loro definizioni i veri oggetti logici esistenti, mentre i segni e l’idea sintattica di dimostrazione erano solo un’utile scrittura di fatti sostanzialmente mentali: che due dimostrazioni relative a concetti diversi avessero la stessa forma sintattica era un fatto quasi accidentale. Per Hilbert invece un concetto si chiariva solo tramite la sua assiomatizzazione categorica, e le definizioni erano del tutto opzionali. Non esistevano concetti esterni che dessero un senso ai segni; il loro significato era formato dai soli assiomi; l’esistenza stessa degli enti matematici si riduceva alla loro consistenza. In Hilbert si intravedevano i tratti di un’autentica trasmutazione sintattica di tutta la matematica, e si delineava l’idea che la stessa intelligenza umana fosse un fatto puramente sintattico, un’idea che anticipa l’intelligenza artificiale. Ma a Hilbert Frege poneva il problema cruciale di chiarire il rapporto tra tale matematica puramente sintattica e la sua applicabilità alle scienze della natura.

Lo scontro tra i due non poteva non essere radicale: Frege poneva al centro della sua analisi l’idea mentale ma oggettiva di verità, che Hilbert voleva invece sostituire del tutto con l’idea sintattica di dimostrazione. La discussione tra i due non trovava una conciliazione e la semplice cartolina con cui Hilbert rispose all’ultima lettera di Frege segnava la fine del xix secolo e l’inizio di un nuovo rapporto tra logica e matematica.

L’intuizionismo

Un altro tipo di riflessione sui fondamenti della matematica che si afferma tra gli ultimi decenni del xix secolo e i primi del xx è quella di impianto costruttivista e intuizionista. Di fronte alla richiesta sempre più pressante di rigore algebrico si levavano voci a difendere il ruolo dell’intuizione geometrica (come per esempio nella scuola italiana di geometria algebrica). Altri autori, come Leopold Kronecker (1823-91) e Jules-Henri Poincaré (1854-1912), pur difendendo le radici intuitive e costruttive della matematica, si andavano allontanando da una concezione geometrica dell’intuizione: come preannunciato da Gauss, era l’aritmetica a diventare il regno dell’a priori. È quindi soprattutto il principio di induzione ad attrarre l’attenzione di Poincaré, per il quale inoltre gli enti matematici dovevano essere definiti predicativamente, evitando cioè quel circolo vizioso tipico dei paradossi nei quali un elemento viene definito facendo riferimento a sé stesso o a un insieme che lo contiene (prassi comune in analisi) invece che a un predicato indipendente.

Ancora più radicale l’intuizionismo di Luitzen Egbertus Jan Brouwer (1881-1966), che considera secondari gli aspetti linguistico-formali e fonda la matematica sull’unico atto intuitivo della one-twoness, alla radice dell’idea di successore tra i naturali. Vittima nobile dell’intuizionismo era la teoria del transfinito attraverso il rifiuto del tertium non datur negli insiemi infiniti, il che implicava la rinuncia in particolare alle dimostrazioni di esistenza non costruttive, in cui si dimostrava l’esistenza di un ente matematico per il fatto che la sua non esistenza generava una contraddizione. Gödel dimostrerà che una logica proposizionale intuizionista e il classico calcolo proposizionale sono mutuamente traducibili e quindi in un certo senso equivalenti, traendone come conseguenza che il divieto essenziale per gli intuizionisti era solo quello delle definizioni impredicative.

Per quanto fascinoso intellettualmente (e anche un po’ preveggente dei teoremi limitativi), l’intuizionismo rendeva estremamente complicata la costruzione di grandi settori della matematica. Per questo, più che tra i matematici, era destinato ad avere fortuna tra gli informatici teorici nella forma di un costruttivismo, per la ragione che gli algoritmi possono solo manipolare enti costruttivamente definiti.

La teoria degli insiemi e l’assioma della scelta

Dopo il 1900 lo studio dell’ipotesi del continuo fu riconosciuto come tema fondamentale della matematica e numerosi furono i tentativi di dimostrarla o di refutarla. Ernst Zermelo (1871-1953) a questo fine presentò un sistema di assiomi per la teoria degli insiemi che affrontava due tipi di problemi: da un lato evitare quelle «molteplicità inconsistenti» che provocavano i paradossi insiemistici, dall’altro consolidare la sua discussa dimostrazione del principio del buon ordinamento. Il sistema assiomatico di Zermelo verrà perfezionato da Abraham Adolf Halevi Fraenkel (1891-1965) ed è per questo noto oggi come ZF.

Il primo obiettivo era raggiunto sostanzialmente modificando la caratterizzazione degli insiemi a partire da una proprietà dei loro elementi, sostituendo la forma ingenua P = {x | p(x)} con la forma P_A = {x ∈ A | p(x)}, così che un predicato p poteva definire un insieme P_A solo agendo come filtro rispetto a un insieme A già definito. A questo punto occorreva ovviamente definire un sistema abbastanza grande di insiemi definibili a prescindere da ogni predicato: l’insieme vuoto, l’insieme formato da uno o due elementi, l’insieme infinito, l’insieme potenza di un insieme già definito.

Il secondo obiettivo era raggiunto tramite l’assioma della scelta secondo il quale, data una famiglia (di qualsivoglia cardinalità) di insiemi (di qualsivoglia cardinalità non nulla), è sempre possibile definire una funzione di scelta che a ogni insieme della famiglia associa un suo elemento. L’assioma era equivalente al principio del buon ordinamento. Questo assioma divenne presto il centro del dibattito poiché attestava l’esistenza di un ente matematico non definito, qualcosa che contrastava soprattutto con le concezioni costruttiviste.

L’assioma era apparentemente tanto ovvio dall’essere stato usato fino allora senza suscitare problemi, ma ora diventava critico per la sua estensione a insiemi transfiniti di qualsiasi cardinalità, in quanto causava conseguenze difficilmente accettabili, quali il buon ordinamento di R o la definibilità di insiemi non misurabili secondo qualsiasi definizione ragionevole di misura (come l’insieme di Vitali), e anche autentici paradossi, come quello di Hausdorff (con l’assioma si poteva ottenere una decomposizione disgiunta di una sfera unitaria dello spazio R³ in 4 insiemi, A, B, C, D tali che A, B, C e B ∪ C erano congruenti e D numerabile).

Nel 1940 Gödel dimostrerà un teorema che garantiva la compatibilità dell’assioma della scelta e dell’ipotesi generalizzata del continuo con i restanti assiomi del sistema ZF (supposti coerenti). Nel 1963 Paul Cohen (1934-2007) dimostrerà che tali risultati non possono essere derivati da ZF. Oggi si può quindi studiare coerentemente tanto il sistema ZF senza assioma della scelta quanto con tale assioma (sistema ZFC).

La nuova teoria degli insiemi, superata la sua fase ingenua, iniziava a caratterizzare il suo rapporto con la logica dei predicati nei termini della distinzione netta tra semantica e sintassi che troverà la sua formulazione moderna negli anni Trenta con Alfred Tarski (1901-83): così il significato di una formula veniva tradotto nella sua “interpretazione” in termini insiemistici, e una interpretazione che soddisfaceva tutti gli assiomi di una teoria assiomatizzata veniva detta un suo modello.

Nel 1929 Gödel aveva dimostrato la completezza (semantica) del calcolo dei predicati e quindi anche l’equivalenza tra consistenza di un sistema di assiomi ed esistenza di almeno un suo modello, garantendo così la sovrapponibilità di verità e dimostrabilità nella logica del primo ordine. Thoralf Albert Skolem (1887-1963) aveva inoltre dimostrato che tra i modelli di una teoria consistente ce ne doveva essere almeno uno numerabile, creando un apparente paradosso quando si considerasse una qualsiasi assiomatizzazione consistente della teoria degli insiemi. Questa doveva ammettere un modello numerabile, in cui valesse anche il teorema secondo cui si poteva costruire in esso un insieme non numerabile. Non era una effettiva contraddizione, poiché la non numerabilità significava formalmente solo l’inesistenza di una corrispondenza biunivoca tra tale insieme e N, la quale corrispondenza altro non era che un insieme anch’esso da definire nel modello numerabile. Semplicemente il paradosso rivelava che nel modello numerabile tale corrispondenza non era costruibile.

Nicolas Bourbaki

Occorre tuttavia osservare come progressivamente queste indagini fondazionali andassero separandosi dall’attività reale dei matematici; dopo la scoperta dei teoremi di incompletezza, il dibattito sui fondamenti delle scuole classiche (logicisti, formalisti, intuizionisti) cessa gradualmente di essere al centro dell’attenzione, per essere sostituito da un impianto fondazionale molto più legato alla prassi consueta del fare matematica. La teoria degli insiemi acquista un ruolo fondazionale del tutto diverso da quello legato alla logica e alla metamatematica con Nicolas Bourbaki. Questo nome appartenuto a un generale borbonico fu assunto come nome collettivo da un gruppo, variato negli anni, di matematici francesi (Henry Cartan, Jean Dieudonné, André Weil, Claude Chevalley ecc.) che dal 1935 iniziarono a pubblicare testi in cui si proponevano di ricostruire una gran parte della matematica sulla base della teoria degli insiemi, distinguendo tre tipi di strutture-base: quelle algebriche, quelle d’ordine e quelle topologiche. In realtà restavano escluse aree importantissime, quali la teoria delle categorie, la teoria degli algoritmi, la combinatoria, la logica, la matematica applicata ecc. In particolare il gruppo appariva indifferente alle discussioni legate ai teoremi limitativi e a risultati come il paradosso di Skolem, ma ebbe grande influenza tanto all’interno del mondo matematico, quanto all’esterno (si pensi alla psicologia cognitiva di Piaget) e influenzò negli anni Cinquanta la didattica elementare, trapiantandovi la teoria degli insiemi come base della formazione matematica.

Era l’ultima incarnazione dell’assiomatizzazione: gli assiomi non erano più certezze evidenti come nell’antichità, né traduzioni formali di proprietà intuitive dei concetti di base come in Dedekind, né lo strumento per catturare il significato di tali concetti in una intelligenza sintattica come in Hilbert, ma solo caratterizzazioni standard di strutture in termini insiemistici.

I teoremi di incompletezza e la computer science

Una delle idee più geniali e ricche di conseguenze del formalismo hilbertiano è la sua Beweistheorie («teoria della dimostrazione», detta anche metamatematica). Essa derivava dal fatto stesso che la matematica formalista era basata su un “linguaggio” di segni e formule tratti da un alfabeto e trattati secondo regole, una struttura cioè analizzabile finitariamente e Gödel collegò tale struttura con l’idea di impronta cantoriana che un tale linguaggio fosse codificabile in N, fosse cioè possibile un’aritmetizzazione della sintassi. Non solo di tale linguaggio formale erano codificabili e decodificabili (algoritmicamente) simboli e formule, ma anche le sequenze di formule: l’aritmetica contenutista diventava un linguaggio con cui parlare della struttura formale dei linguaggi teorici, un metalinguaggio. Le dimostrazioni in particolare non erano sequenze qualsiasi, poiché dovevano obbedire a regole ben precise, regole su formule che nella codifica diventavano funzioni aritmetiche sui numeri di codice delle formule. Per esempio a una regola come il modus ponens che da A e A ⇒ B derivava B, poteva essere associata una funzione aritmetica f_mp, tale che, dette n_A, n_A⇒B e n_B le codifiche delle formule relative, si aveva n_B = f_mp (n_A, n_A⇒B). In generale le proprietà logiche delle formule diventavano proprietà aritmetiche dei loro numeri di codice. Lo studio delle dimostrazioni e dei sistemi formali poteva quindi essere ricondotto a un frammento di aritmetica elementare che studiava queste codifiche. Così per esempio la dimostrazione di consistenza dell’aritmetica poteva essere fatta finitariamente dimostrando contenutisticamente l’indimostrabilità formale di una formula chiaramente assurda, per esempio 0 ≠ 0 (infatti un classico teorema di logica, il cosiddetto teorema dello Pseudo-Scoto, dice che se un sistema di assiomi è inconsistente, allora ogni formula è dimostrabile, e quindi se esiste una formula non dimostrabile il sistema è consistente). Questo si poteva “gödelizzare” tramite il predicato aritmetico ed effettivamente calcolabile Th (codifica aritmetica della proprietà logica di «essere un teorema»), così che una formula t dell’aritmetica formalizzata (codificata nel numero n_t) era un teorema se e solo se aritmeticamente era vero Th(n_t). A questo punto per dimostrare la consistenza dell’aritmetica formalizzata bastava verificare che il numero n_0≠0 non soddisfacesse il predicato aritmetico Th. La dimostrazione della consistenza dell’aritmetica formalizzata diveniva così un problema di aritmetica contenutistica.

Nel 1930 tra i più brillanti matematici influenzati dal programma di Hilbert c’era Gödel, anch’egli interessato ai problemi della verità e della consistenza. Supponendo che l’aritmetica formalizzata fosse consistente, era evidente che la formula ￢Th(n_t) era anch’essa una formula aritmetica g dipendente dal numero n_t e quindi n_g era una funzione aritmetica di n_t, n_g = φ(n_t). Gödel riuscì a determinare una formula d che rappresentava un punto fisso per tale funzione aritmetica, n_d = φ(n_d): d era quindi proprio la formula ￢Th(n_d), cioè nella sua codifica d diceva di essere non dimostrabile. A questo punto se d era vera allora non era dimostrabile e se era falsa allora era dimostrabile. Ma d’altra parte valeva la proprietà di correttezza e quindi ogni formula dimostrabile era anche vera. Ne conseguiva che d poteva solo essere vera ma non dimostrabile: l’aritmetica formalizzata, se consistente, non era quindi semanticamente completa. Ovviamente, ￢d essendo falso non era dimostrabile: veniva meno quindi anche la completezza sintattica e la decidibilità (primo teorema di incompletezza). Si tratta di una incompletezza essenziale: la possibile aggiunta di d (che era risultato essere vero) tra gli assiomi lo renderebbe dimostrabile, ma cambierebbe la codifica (che dipende dal sistema di assiomi) e quindi il predicato di dimostrabilità diventerebbe un certo Th ′, e si determinerebbe un diverso punto fisso d′′ che risulterebbe vero ma non dimostrabile.

Questo risultato rendeva impossibile ogni dimostrazione aritmetica formale della consistenza della aritmetica, supposta consistente (secondo teorema di incompletezza). Infatti il primo teorema basato sulla ipotesi di consistenza dimostrava la verità di d. Se fosse esistita una dimostrazione di consistenza dell’aritmetica a partire dagli assiomi dell’aritmetica, unendo le due dimostrazione si sarebbe avuta una dimostrazione di d, risultato precluso dal primo teorema di incompletezza.

Pur non essendo una vera antinomia, questo teorema mostrava una «somiglianza di famiglia» con altri risultati paradossali quali il paradosso del mentitore (e anche con la procedura diagonale di Cantor), tutti legati alla possibilità di rappresentare verità, essere e negazione, e alla mancata distinzione tra linguaggio oggetto e metalinguaggio: nei teoremi di incompletezza la metamatematica era il metalinguaggio (aritmetica non formalizzata) con cui parlare delle proprietà formali dell’aritmetica formalizzata, e l’aritmetica funzionava quindi sia come linguaggio oggetto sia come metalinguaggio. Conseguenza ulteriore era che nessuna teoria abbastanza potente da contenere l’aritmetica ammetteva una assiomatizzazione categorica al primo ordine: esistevano sempre modelli non standard. Se si passava alla logica del secondo ordine era possibile costruire assiomatizzazioni categoriche. Si delineava quindi l’alternativa tra fondare la matematica su una logica del primo ordine, pagando il prezzo della incompletezza e della non categoricità delle teorie matematiche, oppure fondarla su una logica del secondo ordine, la quale consentiva assiomatizzazioni categoriche ma era già di fatto matematica (teoria degli insiemi) e non logica, e il prezzo diventava l’incompletezza anche della stessa logica.

La teoria degli insiemi appariva “schizoide”, una specie di Dr. Jekyll e Mr. Hyde. Era ancora assoluta, ma non più come nella fase “ingenua” in cui appariva indistinguibile dalla logica di Frege: ormai si presentava con Bourbaki come base linguistica e concettuale indiscussa di tutta la matematica, oppure in logica come la semantica del calcolo dei predicati. Ma d’altra parte, sia i teoremi limitativi sia il paradosso di Skolem e il dibattito sull’assioma della scelta ne minavano la assolutezza come teoria: era anch’essa una teoria matematica assiomatizzata e andava anch’essa sottomessa alla analisi metamatematica in termini di incompletezza e di distinzione tra sintassi e semantica.

Il calcolabile e la macchina universale

Negli anni Trenta si verifica una piccola, ma qualitativamente eccezionale, emigrazione di scienziati dalla Mitteleuropa (e anche dall’Italia), oppressa dal nazifascismo, agli Stati Uniti, verso le università e l’Institute of Advanced Studies di Princeton: Gödel, Neumann, Weyl tra i matematici, Einstein, Fermi, Wigner tra i fisici. Tra i matematici c’erano alcuni dei migliori seguaci di Hilbert i quali continuarono a lavorare nella tradizione formalista, in particolare analizzando un concetto chiave della matematica da Cantor a Hilbert: quello di algoritmo, un concetto molto usato ma restato fino ad allora solo intuitivo. Su questo tema si impegnarono anche logici e matematici angloamericani, come Alan Turing (1912-54) e Alonzo Church (1903-95), anch’essi influenzati dal formalismo hilbertiano. La formalizzazione di tale concetto portò negli anni Trenta e Quaranta a innumerevoli soluzioni, tra cui le macchine di Turing, le funzioni ricorsive, il λ-calcolo.

Anche negli algoritmi la semantica aveva un doppio regime: il significato di una primitiva del linguaggio algoritmico era built-in, dato dalle regole del suo trattamento nel formalismo (nelle routine del compilatore/interprete per i linguaggi di programmazione), mentre il significato del segno di un identificatore in un particolare algoritmo o programma applicativo era fornito dal suo uso nel programma stesso, e scopo della programmazione era di catturare tramite il codice del programma il significato inteso dal programmatore. La formalizzazione del concetto di algoritmo permetteva di definire un problema decidibile quando esisteva un algoritmo per risolverlo terminante sia nei casi positivi sia negativi, semidecidibile quando nei casi negativi poteva non terminare, indecidibile altrimenti. Una distinzione fondamentale: la stessa esistenza dei teoremi limitativi deriva dall’esistenza di problemi semidecidibili.

Da queste indagini risultava chiaro in primo luogo che tutti i formalismi erano equivalenti tra di loro nel senso che, per esempio, ogni funzione calcolabile tramite una macchina di Turing lo era anche mediante le funzioni ricorsive e viceversa. In secondo luogo non si riusciva a trovare nessuna funzione intuitivamente calcolabile che non fosse calcolabile in tali formalizzazioni. Da queste due osservazioni si ipotizzò che tali formalizzazioni catturassero completamente il senso della computabilità effettiva (tesi di Church: ogni funzione effettivamente calcolabile è computabile da una macchina di Turing o da un altro formalismo equivalente).

Inoltre gli algoritmi risultavano numerabili poiché esprimibili con una codifica della loro descrizione formale, che era una espressione finita in uno specifico alfabeto (relativo al formalismo prescelto), ed era possibile costruire l’algoritmo (macchina) universale, un algoritmo cioè, che avendo in input la codifica di un algoritmo particolare e i dati, simulasse il funzionamento di tale algoritmo con quei dati come input: per esempio una macchina di Turing capace di leggere e interpretare nella esecuzione le regole con cui era descritta una qualsiasi macchina di Turing specifica e applicarle ai dati.

Così prendeva corpo l’idea del calcolabile, come «insieme di tutti gli algoritmi», in fondo semplicemente tutto ciò che si può fare manipolando segni secondo regole, un concetto che, contrariamente a quello che si potrebbe sospettare, ammetteva un limite insuperabile, assoluto, indipendente da operazioni, simbolismi, regole utilizzabili. L’idea del calcolabile e della macchina universale prolungava per così dire il ruolo cantoriano di N (la capacità di codificare qualunque insieme di oggetti finitamente esprimibili in qualsivoglia alfabeto e di essere codificato in qualunque alfabeto) estendendolo da una semplice capacità di rappresentare gli aspetti statici di una characteristica universalis a una capacità di fornire anche un calculus ratiocinator che ne traducesse gli aspetti dinamici, algoritmici.

Altri teoremi limitativi

La stessa struttura argomentativa intorno alla rappresentazione apparsa nei teoremi di incompletezza compariva anche in altri teoremi limitativi scoperti negli anni Trenta: il teorema dell’alt dovuto a Turing (il problema di decidere se un certo algoritmo con un certo input termina è solo semidecidibile), il teorema di Church (il problema della dimostrabilità per le formule del calcolo dei predicati del primo ordine è solo semidecidibile), il teorema di Tarski (il problema di decidere se una formula aritmetica è vera è indecidibile). Gli stessi teoremi di incompletezza ammettevano una maggiore generalità e sancivano come l’argomentazione matematica non fosse riducibile ad alcuna concezione algoritmica dell’idea di dimostrazione. Questi teoremi configurano uno dei problemi fondazionali della matematica più rilevanti aperti a tutt’oggi, ponendo interrogativi sulla natura della dimostrazione e sul rapporto tra enti matematici e segni, tanto che è opinione comune che i teoremi di incompletezza abbiano sancito il fallimento del programma di Hilbert.

In realtà sarebbe più corretto dire che Hilbert ha fallito come Cristoforo Colombo, il quale fallì nella ricerca di una via nuova per raggiungere il vecchio mondo, le Indie, ma scoprì il Nuovo Mondo. Così Hilbert cercava una via nuova per ricostruire tutta la matematica tradizionale: non riuscì nell’impresa, ma scoprì anch’egli un nuovo mondo, delineando una matematica sintattica che non poteva essere tout court la veste nuova della vecchia matematica, ma era un’altra cosa.

La matematica in un certo senso si sdoppiava: quella tradizionale non aveva remore a trattare l’infinito, riduceva il formalismo al bourbakismo e restava insensibile ai risultati sconcertanti dei teoremi di incompletezza. La nuova matematica sintattica si proponeva invece come teoria degli algoritmi e come computer science.

La computer science

Era questo il modello teorico elaborato in forma tecnologica negli anni 1944-46 da Turing e John von Neumann (1903-1957) abbastanza indipendentemente per costruire il computer, epifania della macchina universale, il cui carattere assoluto la rende del tutto incommensurabile con i calcolatori precedenti (da Pascal e Leibniz a Babbage).

All’origine del computer vi era anche la nascente elettronica moderna, che negli usa era già all’avanguardia negli anni Trenta (si pensi al televisore). Ma il ruolo dell’anima elettronica è molto diverso dal ruolo dell’anima logico-matematica della computer science. Le diverse generazioni del computer sono infatti caratterizzate dai crescenti livelli di integrazione e miniaturizzazione elettronica (si dice che ogni cinque anni i calcolatori diventino dieci volte più piccoli, dieci volte più veloci e dieci volte più economici), mentre si può affermare che i computer costruiti negli ultimi settant’anni sono praticamente tutti basati sulla stessa architettura, quella di von Neumann. Alla storia del computer sono ascrivibili due fasi nettamente distinte: da Pascal all’ultima guerra è caratterizzata da esemplari sostanzialmente unici, negli ultimi settant’anni da milioni di riproduzioni della stessa macchina sintattica, del cui divenire dà conto l’elettronica (ed è forse quanto di più “eracliteo” la storia ci abbia mai regalato), e della cui essenza danno conto la logica e la matematica (e appare quanto di più immutabile e “parmenideo” la civiltà moderna abbia creato).

La matematica e il suo tempo

È difficile, quasi impossibile, fare la storia della matematica contemporanea, in quanto caratterizzata da una specializzazione estrema: si dice che dopo Hilbert nessun matematico possa presumere di averne una visione complessiva. Si possono certo fare elenchi delle aree di ricerca più diffuse, ma appare molto arduo dare della matematica contemporanea una descrizione sintetica. Si può però sostenere che l’affermarsi del linguaggio logico, del formalismo, della teoria della calcolabilità caratterizzino negli ultimi cent’anni una matematica solidamente strutturata su una base sintattica, nonostante le questioni fondazionali aperte (dai teoremi limitativi all’ipotesi del continuo) ripropongano il problema del rapporto tra la matematica e i segni, e grandi matematici, da Poincaré a Weyl, abbiano criticato radicalmente le estreme tendenze logiciste e formaliste.

Riguardo al rapporto tra matematica e scienza, nel xx secolo la matematica, a mano a mano che si esauriva il dibattito sui fondamenti, ha assunto sempre più il ruolo di semplice strumento linguistico delle scienze, facendo inoltre proprio il precetto pragmatico e autogiustificativo che «la matematica è quello che fanno i matematici». Oggi nelle indagini di tipo logico-formale sui fondamenti sembra che l’unico scopo sia trovare un sistema di assiomi che permetta di salvaguardare il lavoro attuale dei matematici, per esempio cercando di aggiungere agli assiomi classici di ZF qualche assioma che permetta di dimostrare o refutare l’ipotesi del continuo o l’assioma della scelta.

Questa riduzione della matematica, paradossalmente strumentale e isolazionista allo stesso tempo, è documentata in forme diverse, in vari indirizzi del pensiero contemporaneo, dal neopositivismo alla filosofia analitica. Oggi l’approccio più seguito resta quello attribuito a Willard Van Orman Quine (1908-2000), per il quale la scienza è una rete di teorie, osservazioni, principi, strettamente legati tra di loro e vincolati al contorno dai fatti empirici che costringono le parti più interne (e quindi anche la matematica e forse la stessa logica) ad adeguarsi a essi nel modo più economico ed estetico possibile. Ricorre spesso d’altra parte il richiamo a una inesauribilità del pensiero matematico, alla sua irriducibilità al formalismo e all’inevitabilità dell’intuizione matematica. Le stesse proposizioni aritmetiche indecidibili introdotte da Gödel non sono più solo strane asserzioni logiche, ma si ritrovano anche nella normale teoria dei numeri e in capitoli della computer science. Inoltre la matematica sembra anche teoricamente anticipare le sue stesse applicazioni: gli spazi di Hilbert sono stati studiati prima del loro uso in meccanica quantistica, il calcolo tensoriale prima del suo uso nella relatività generale, e il fisico Eugene Wigner si interrogava sulla «irragionevole efficacia della matematica nelle scienze della natura». Tuttavia da queste prese di posizione si arriva oggi solo a teorizzare una matematica quasi-empirica, affine alla fisica, oppure a esaltare il carattere non razionale del genio matematico, ma la maggioranza dei matematici si ritiene estranea alle questioni fondazionali, logiche o filosofiche, formali o intuizioniste che siano.

Tutte queste tendenze hanno in comune l’appannarsi del ruolo conoscitivo generale, autonomo e peculiare, della matematica, e infatti gli unici temi che vengono oggi avanzati per difendere l’importanza della formazione matematica sono la sua utilità nelle applicazioni e nell’esercizio logico, o il suo fascino intellettuale. Manca una vera filosofia della matematica: non a caso forse l’unico vero filosofo della matematica del xx secolo è stato Ludwig Wittgenstein.

Ringraziamenti. Ad alcuni amici che mi hanno aiutato con i loro consigli e le loro critiche: Vieri Benci, Alessandro Bianchi, Bruno D’Amore, Gianbattista Formica, Paolo Freguglia, Gabriele Lolli.