stato

stato

stato elemento descrittore di un processo che muta in modo discreto; a ogni suo mutamento, che avviene per “passi” successivi, lo stato descrive i valori delle variabili coinvolte e l’intero processo è così rappresentabile come un insieme di cambiamenti di stato. Tali cambiamenti avvengono sulla base delle regole sintattiche che definiscono il processo e sono univocamente definiti a ogni stato nel caso di processi deterministici, o definiti in modo non univoco nel caso di processi non deterministici; in quest’ultimo caso può essere definita la probabilità di transito da uno stato a ciascuno dei possibili stati successivi e il processo viene detto probabilistico. In tutti questi casi la descrizione degli stati e delle possibili transizioni da uno stato al successivo (o a uno dei successivi) è generalmente fatta attraverso un grafo degli stati che esprime ex ante l’evoluzione del processo. Se invece il processo evolve in modo caotico non esiste una possibilità di descriverne l’evoluzione da stati ex ante, ma solo quella di rappresentare ex post, con un grafo o una tabella, come esso sia andato evolvendosi.

Il calcolo di una espressione o una catena deduttiva in un → sistema formale possono essere visti come una sequenza di stati, in cui a ogni passaggio si modifica il valore dell’espressione scritta, fino a giungere al risultato finale; i passaggi sono transizioni da uno stato del calcolo a un altro e sono possibili in base alle proprietà delle operazioni o alle regole grammaticali che definiscono il sistema formale. Analogamente, nella costruzione degli algoritmi si considerano a ogni passo i valori di ciascuna variabile e questo controllo consente di stabilire la correttezza della sequenza di istruzioni costituenti l’algoritmo: il problema da risolvere e il relativo algoritmo risolutivo sono così rappresentati come un cammino sul grafo degli stati che muove da una configurazione iniziale, data dai valori noti delle variabili (stato iniziale) per giungere al risultato (stato finale). L’algoritmo è un percorso sul grafo degli stati dallo stato iniziale allo stato finale di tipo lineare: ogni nodo del grafo, che non sia quello iniziale o quello finale, ha un solo arco in ingresso e un solo arco in uscita.

Per esempio, l’algoritmo che fornisce i primi 10 elementi della successione di → Fibonacci, il cui elemento generico è l’intero dato dalla somma dei due precedenti, può essere formato da un ciclo iterativo come il seguente (integer è il tipo di dato delle variabili: esse assumono valori interi; il simbolo ≔ indica l’assegnazione di valore alla variabile ed è qui utilizzato per distinguerlo dal segno di uguaglianza):

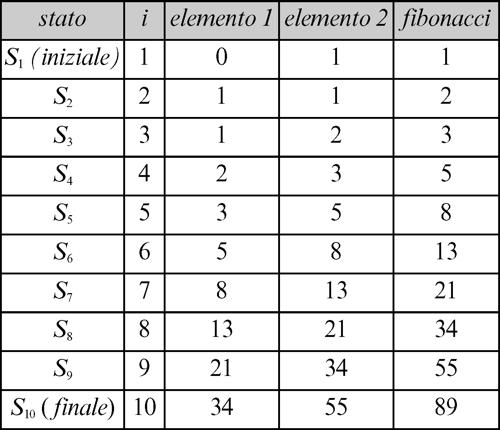
Al termine di ogni ciclo lo stato S_i del calcolo relativo alle variabili i, elemento1, elemento2, fibonacci, è ogni volta modificato; la variabile fibonacci contiene a ogni passo l’elemento della successione.

La corrispondente evoluzione degli stati del calcolo può essere rappresentata in tabella:

Il passaggio da uno stato al successivo avviene in base a un’istruzione e l’algoritmo può essere equivalentemente descritto elencando le azioni da compiere (istruzioni) per giungere al risultato, cioè dal → programma, oppure elencando gli stati che ogni volta si presentano, da quello iniziale a quello finale, che è il risultato. Le due descrizioni devono avere una caratteristica di dualità affinché la procedura definita sia effettivamente in grado di far ottenere il risultato che si intendeva ricercare.

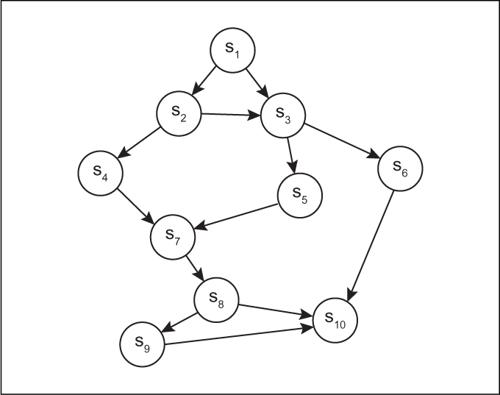
Poiché risolvere un problema vuol dire passare da una situazione iniziale a una situazione finale, il processo risolutivo può essere descritto come un cammino lineare sul suo grafo degli stati: ogni stato del problema indica una situazione che può verificarsi, a partire da quella iniziale, e ogni transizione indica una elaborazione delle informazioni possedute o il compimento di azioni o calcoli.

Ogni percorso che va dallo stato iniziale S₁ allo stato finale S₁₀ è una soluzione del problema. Le rappresentazioni della possibili transizioni di stato sono particolarmente utili per evidenziare il funzionamento di un → automa, per esempio un automa a stati finiti.