spazio

spazio

Molto più che tre dimensioni

Con il termine spazio si intendono molte cose diverse: quando si dice che un oggetto occupa un certo spazio, esso può essere inteso come l’ambiente in cui scambiamo le nostre esperienze, viviamo e ci muoviamo. Se però si parla di ‘guerre stellari’ ci si riferisce a uno spazio grande quanto il Sistema Solare o l’Universo intero.

Ma lo spazio è anche un concetto matematico, un ‘luogo’ astratto in cui si possono effettuare alcune operazioni e stabilire determinate relazioni. Ci sono dunque diversi tipi di spazio, a seconda del problema che si vuole risolvere

Lo spazio nell’esperienza quotidiana e nelle scienze

Gli esseri umani percepiscono la realtà circostante attraverso i sensi: vista, odorato, udito, tatto, gusto permettono di esplorare lo spazio esterno, ma poi è la mente che elabora i segnali ricevuti dall’ambiente. Di volta in volta, infatti, possono interessare aspetti differenti e l’esperienza sensoriale non è mai un fatto indistinto. Lo spazio quindi indica l’ambiente in cui siamo collocati noi stessi e gli oggetti che ci circondano, che è anche quello in cui ci muoviamo.

Nelle scienze il termine spazio assume varie accezioni: per esempio, in geometria interessano le lunghezze, le forme, ma non certo il colore o l’odore degli oggetti; se si vuole calcolare la velocità e la direzione da imprimere a un missile affinché metta in orbita un satellite attorno alla Terra, i calcoli matematici non possono trascurare la forza di gravità. Lo spazio fisico ha perciò caratteristiche ulteriori rispetto a quello matematico. In generale, occorre quindi precisare di quale spazio si sta parlando, rispetto al problema di cui ci si occupa.

Le tre dimensioni

fig.

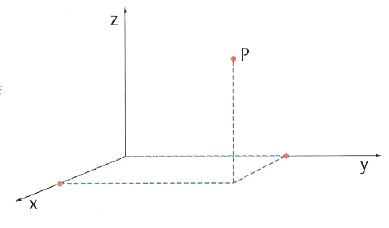
Lo spazio dell’esperienza quotidiana ha tre dimensioni che, per gli oggetti di uso comune, sono dette lunghezza, larghezza e altezza. In termini matematici, ogni punto dello spazio è individuato attraverso tre numeri, una volta fissati tre assi, indicati con le lettere x, y, z. I tre assi costituiscono il sistema di riferimento e i tre numeri sono le coordinate del punto P = x, y, z (v. fig.).

Talvolta, però, per spazio si intende qualcosa di diverso da questa astrazione matematica. Se si dice che è stata inviata una sonda nello spazio, si fa riferimento a una regione priva dell’atmosfera che avvolge la Terra. In tale caso si sta parlando di spazio interplanetario o addirittura interstellare; uno spazio lontano, distante più di 100 km dalla superficie terrestre, dove non c’è più atmosfera.

Movimenti nello spazio

Lo spazio a tre dimensioni è l’ambiente in cui la fisica classica studia il moto dei corpi e le sue cause. In tale spazio fisico ci si può spostare con continuità. In questo senso, lo spazio, oltre che un ambiente, è anche un concetto fisico che, unito a un altro concetto fondamentale, il tempo, definisce la velocità.

Per velocità di un corpo (v) si intende, infatti, il rapporto tra lo spazio percorso (s) dal corpo e il tempo impiegato a percorrerlo (t): v = s/t. Usualmente la velocità viene misurata in chilometri all’ora (km/h) oppure in metri al secondo (m/s).

Spazio e tempo

Dopo la teoria della relatività formulata da Einstein, lo spazio e il tempo non sono più due concetti separati e si parla di spazio-tempo come ambiente generale in cui studiare il moto dei corpi.

Occorre tenere presente che le distanze che solitamente si percorrono sono brevi, irrilevanti in confronto alle dimensioni dell’Universo; anche le velocità che si considerano usualmente sono molto più piccole rispetto alla velocità della luce nel vuoto (circa 300.000 km/s). In tali circostanze, le dimensioni degli oggetti non cambiano: la lunghezza di un’automobile da corsa è la stessa sia quando è ferma sia quando sfreccia a 300 km/h. La teoria della relatività ha però chiarito che tale invarianza non è più valida quando la velocità diventa enorme, prossima a quella della luce nel vuoto. In tale situazione, un oggetto subisce una contrazione nella direzione del moto: cambiano le sue misure e per descrivere un evento non sono più sufficienti tre coordinate, ma ne servono quattro, giacché occorre aggiungere la coordinata del tempo.

Oltre la terza dimensione

Aggiungendo alle tre coordinate x, y, z, la coordinata t relativa al tempo lo spazio ha in tutto quattro dimensioni. Ma in matematica non ci si ferma qui: si definiscono anche spazi a 5, 6, …, n dimensioni, quante si vogliono, perfino infinite!

Non ci si sta avventurando nella fantascienza. Vediamo perché. Consideriamo meglio il significato di dimensione: un ambiente ha dimensione n se sono necessari e sufficienti n numeri per identificare ogni suo oggetto.

Possiamo così dire che, per esempio, l’autostrada del Sole, che collega Milano con Napoli, ha dimensione 1 perché è sufficiente un numero (la distanza in chilometri da Milano) per individuare un suo punto. Facendo la spesa al supermercato si trova invece l’esempio di uno spazio a più dimensioni. Infatti, ogni articolo ha un’etichetta con un codice letto da un dispositivo ottico. Al codice corrispondono diverse informazioni numeriche utilizzate per la gestione del magazzino: il tipo di articolo; il codice del fornitore; la quantità in magazzino; il costo; il prezzo di vendita. Ogni prodotto corrisponde così a un punto in uno spazio a 5 dimensioni.

Spazi matematici

Con le 5 coordinate assegnate a ogni prodotto si possono effettuare alcune operazioni. Se per esempio un cliente lo acquista, la quantità in magazzino di quell’articolo viene diminuita di 1. Così, l’insieme dei prodotti del supermercato costituisce uno spazio, nel senso matematico del termine. In matematica, infatti, lo spazio non è qualcosa che necessariamente deve essere visibile; è piuttosto un ambiente in cui sono definiti oggetti con certe proprietà, legati da determinate relazioni e con cui si possono effettuare operazioni.

Esiste un’ampia varietà di possibili spazi matematici. Tra i più importanti ci sono lo spazio topologico e quello proiettivo.

Lo spazio topologico è l’ambiente in cui non interessano le distanze effettive tra punti e oggetti, quanto il modo in cui le diverse parti sono tra loro collegate e connesse. Un tipico esempio di problema topologico è quello della colorazione di una carta geografica. Quanti colori servono per colorare una carta in modo tale che due stati confinanti abbiano sempre colori diversi? Il problema riguarda la ‘vicinanza’, ma non in senso metrico. Ebbene, un teorema dimostrato alla fine del 20° secolo afferma che sono sufficienti quattro colori.

Lo spazio proiettivo è l’ambiente in cui si realizza la visione. In questo caso si compie un’astrazione: linee parallele sono viste come convergenti e si verificano fenomeni interessanti. Per esempio le figure umane stilizzate presenti nell’immagine hanno uguali dimensioni, eppure le linee prospettiche convergenti le fanno percepire come se fossero molto diverse l’una dall’altra.

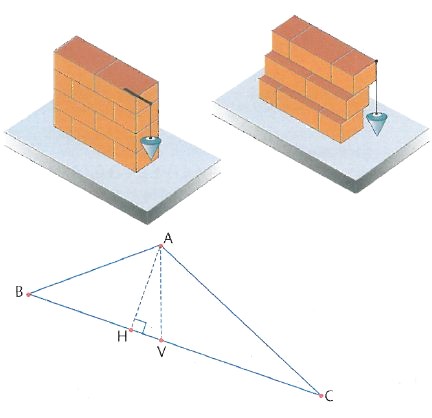
La perpendicolare tra fisica e matematica

fig.

Quando un muratore costruisce un muro verifica che esso sia perpendicolare rispetto al pavimento in modo tale che il peso di ogni mattone si scarichi su quello sottostante e la parete non crolli. Per fare ciò usa un filo a piombo, che indica la direzione verticale. Talvolta si confonde il concetto spaziale fisico di verticale – che è la direzione perpendicolare rispetto alla superficie terrestre – con quello matematico di altezza, che è la direzione perpendicolare, cioè a 90°, rispetto a una data direzione, qualunque essa sia. Per esempio, nel triangolo ABC, l’altezza del triangolo rispetto alla base BC non è il segmento AV, ma il segmento AH (v. fig.).