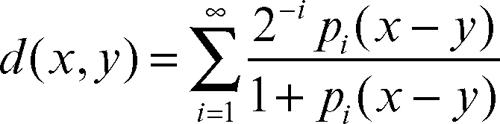spazio vettoriale topologico

spazio vettoriale topologico

spazio vettoriale topologico spazio vettoriale X dotato di una → struttura topologica τ tale che le operazioni di addizione e di moltiplicazione per uno scalare risultino continue (alcuni autori aggiungono anche la condizione che ogni punto sia un insieme chiuso, e ciò implica che lo spazio sia di → Hausdorff).

Sono particolarmente importanti gli spazi vettoriali topologici localmente convessi, cioè quelli che hanno una base di intorni dell’origine formata da insiemi convessi. La loro topologia è individuata da una famiglia di seminorme, cioè di funzionali p(x) che soddisfano le proprietà:

a) p(x + y) ≤ p(x) + p(y) (subadditività)

b) p(αx) = |α|p(x)

(Se si aggiunge la condizione di annullamento p(x) = 0 se e solo se x = 0 una seminorma diviene una norma). Una famiglia P di seminorme si dice separante se ∀x ≠ 0 esiste p ∈ P tale che p(x) ≠ 0. Per esempio, in Rⁿ una famiglia di seminorme è data da p_k(x) = |x_k|, dove x_k è la componente k-esima di x.

Si consideri un insieme convesso A che sia assorbente, cioè sia tale che ∀x ∈ X, ∃t > 0: x ∈ tA, dove l’insieme tA è dato da {x: ∃a ∈ A, tale che x = ta}. Il funzionale di Minkowski μ_A(x) dell’insieme A è definito da: μ_A(x) = inf{t > 0: t⁻¹x ∈ A}. Se A è anche bilanciato, cioè se tA ⊂ A per ogni t con |t | ≤ 1, il funzionale di Minkowski è una seminorma in X. Viceversa, data una famiglia separante P di seminorme in uno spazio vettoriale X, l’insieme di tutte le intersezioni finite degli insiemi

forma una base di intorni dell’origine che rende X spazio vettoriale topologico localmente convesso.

Se P è numerabile, la topologia è metrizzabile e una distanza d è data da

Per esempio, se Ω è un aperto di Rⁿ, lo spazio C(Ω) formato dalle funzioni f continue in Ω può essere dotato delle seminorme

dove {K_n} è una famiglia di → compatti tali che K_n sta all’interno di K_n+1 e la cui unione è Ω. Nella metrica sopra indicata, C(Ω) risulta completo: si dice che è uno spazio di Fréchet, cioè è uno spazio localmente convesso completo in una metrica invariante per traslazioni. Lo stesso si può dire per lo spazio C ^∞(Ω), con le seminorme