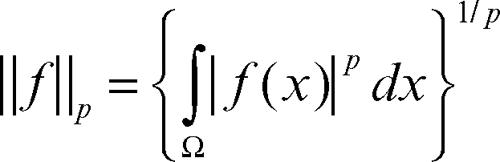spazio Lp(Ω)
spazio Lp (O)
spazio Lp(Ω) con Ω sottoinsieme misurabile di Rn, spazio vettoriale delle funzioni ƒ misurabili secondo Lebesgue per le quali l’integrale
Se p ≥ 1, lo spazio è normato, con norma
e completo in tale norma e quindi è uno spazio di → Banach. Se p ∈ (0, 1), lo spazio è ancora vettoriale, ma l’espressione precedente non rappresenta una norma, perché non è soddisfatta la disuguaglianza triangolare. Lo spazio L∞(Ω) costituito dalle funzioni essenzialmente limitate è di Banach con norma
La notazione «ess sup» che compare nella formula indica l’estremo superiore essenziale della funzione |ƒ(x)|, cioè l’estremo superiore a meno di un insieme di misura nulla:
Si osserva che gli elementi di Lp sono in realtà classi di equivalenza di funzioni rispetto alla relazione di uguaglianza quasi ovunque (q.o.), cioè s’intendono equivalenti due funzioni che coincidono, escluso al più un insieme di misura nulla secondo Lebesgue. Se 1 ≤ p ≤ q ≤ ∞ e Ω è limitato, risulta Lq(Ω) ⊂ Lp(Ω), con immersione continua; altrimenti non esiste alcuna inclusione. Tuttavia se x ∈ Lq(Ω) ∩ Lp(Ω), allora x ∈ Lr(Ω), per ogni r ∈ (p, q).
Se p e p′ soddisfano l’uguaglianza
essi si dicono esponenti coniugati; per p < ∞ il duale di Lp(Ω) è Lp′ (Ω), e quindi se 1 < p < ∞ gli spazi Lp sono riflessivi. Se g ∈ Lp′, risulta
(→ Hölder, disuguaglianza di). In particolare, lo spazio L2(Ω) è uno spazio di → Hilbert.