solido platonico
solido platonico
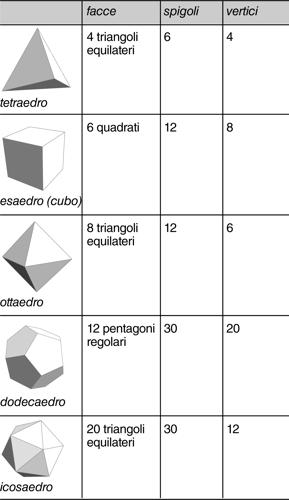
solido platonico o poliedro regolare, poliedro convesso le cui facce sono poligoni regolari tra loro congruenti e i cui angoloidi ai vertici sono tutti della stessa ampiezza. Mentre esistono infiniti poligoni regolari, i poliedri regolari sono solo di cinque diversi tipi. Infatti, in ogni vertice di un qualsiasi poliedro devono concorrere almeno tre poligoni regolari tali che la somma degli angoli che concorrono sia minore di 360° (altrimenti si formerebbe una pavimentazione piana) e perciò l’angoloide di un solido platonico può avere per facce solo triangoli equilateri, quadrati e pentagoni regolari. Infatti, già componendo tra loro degli esagoni regolari, non si può formare alcun solido perché gli esagoni tassellano il piano (→ tassellazione).
La singolarità della scoperta che esistono soltanto cinque poliedri regolari, avvenuta certamente prima di Platone, stupì i matematici greci. Seguendo una tradizione pitagorica (→ pitagorismo), incline a identificare i principi ideali della realtà con i principi della razionalità matematica e geometrica, Platone, nel dialogo Timeo, espose la teoria secondo la quale gli elementi che costituiscono l’universo hanno la forma dei cinque solidi regolari: il tetraedro è la forma del fuoco, l’ottaedro è quella dell’aria, l’icosaedro quella dell’acqua, il cubo, forse per la sua dote di stabilità, quella della terra. All’ultimo solido regolare, il dodecaedro, con facce pentagonali, spetta un ruolo particolare, perché, scrive Platone: «C’era tuttavia una quinta combinazione e Dio l’usò per decorare l’universo». Per questa loro interpretazione come forme degli elementi costitutivi dell’universo, i poliedri regolari sono ancora oggi chiamati solidi platonici.
Nella → dualità tra poliedri (corrispondenza che a un poliedro P associa un poliedro P′ tale che il numero delle facce e dei vertici di P sia uguale, rispettivamente, al numero dei vertici e delle facce di P′ ), il tetraedro risulta autoduale (duale di sé stesso), l’esaedro ha per duale l’ottaedro (e viceversa), il dodecaedro ha per duale l’icosaedro (e viceversa). Data la loro struttura regolare, i solidi platonici presentano numerose → simmetrie centrali, assiali, planari e rotazionali. Le simmetrie di ciascun solido platonico formano un gruppo rispetto all’operazione di composizione di trasformazioni, detto gruppo di simmetria del poliedro. I gruppi di simmetria di due poliedri regolari duali coincidono, a meno di un isomorfismo e sono i seguenti:
• gruppo di simmetria del tetraedro, formato da 24 elementi, di cui 12 sono simmetrie planari, una è l’identità, e altre 11 sono rotazioni: otto rotazioni di ordine 3 e tre rotazioni di ordine 2; l’identità e le undici rotazioni costituiscono un sottogruppo di 12 elementi detto gruppo tetraedrale;
• gruppo di simmetria del cubo, formato da 48 elementi: 24 sono rotazioni fra le quali è compresa l’identità e insieme costituiscono un sottogruppo detto gruppo ottaedrale (perché è lo stesso anche per l’ottaedro). A queste si aggiungono 9 simmetrie planari, 15 composizioni di rotazioni con simmetrie. Isomorfo a questo è il gruppo di simmetria dell’ottaedro;
• gruppo di simmetria del dodecaedro, formato da 120 elementi: l’identità, 24 rotazioni di ordine 5, 20 rotazioni di ordine 3 e 15 rotazioni di ordine 2 costituiscono insieme il sottogruppo detto gruppo icosaedrale (perché è lo stesso per l’icosaedro). A queste si aggiungono altre 60 tra simmetrie e opportune composizioni con rotazioni. Isomorfo a questo è il gruppo di simmetria dell’icosaedro.
Per la distinzione tra gruppo delle simmetrie del tetraedro (ottaedro, icosaedro) e gruppo tetraedrale (ottaedrale, icosaedrale) si veda il lemma → simmetria, gruppo di (di una figura).
In uno spazio euclideo di dimensione n ≥ 4, l’equivalente del poliedro regolare è detto → politopo regolare. Se n = 4 si hanno sei politopi regolari, se n = 5 si hanno tre politopi regolari, gli analoghi del tetraedro regolare, del cubo e dell’ottaedro regolare.