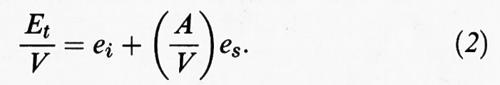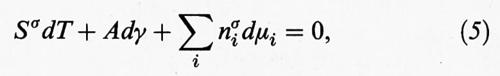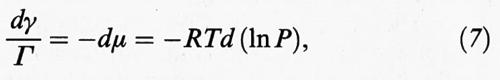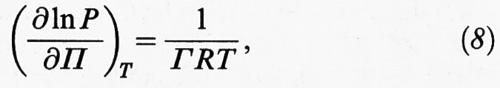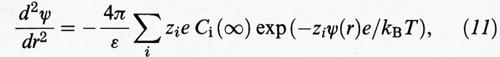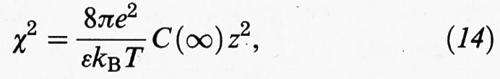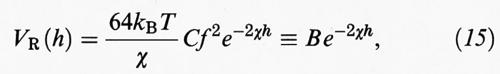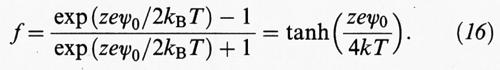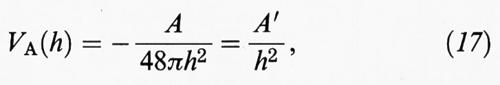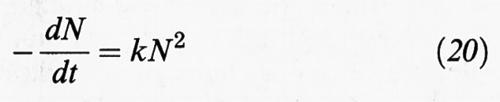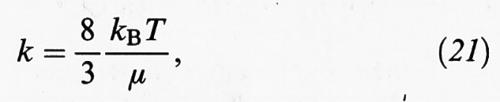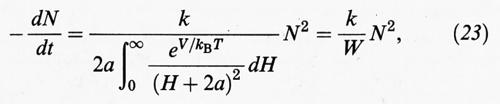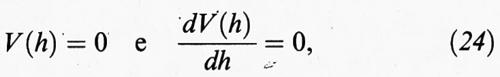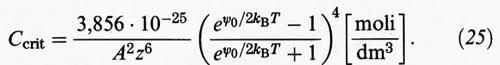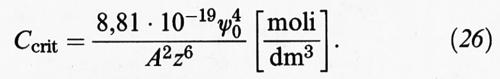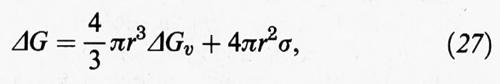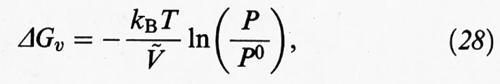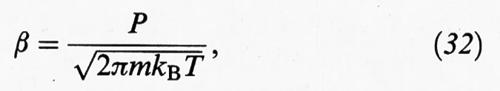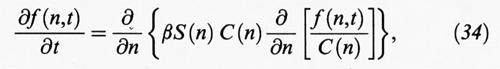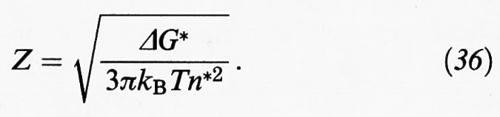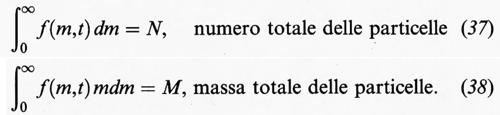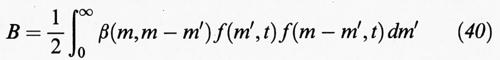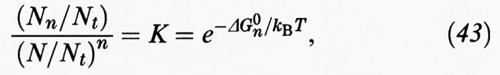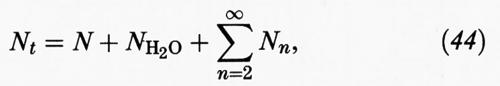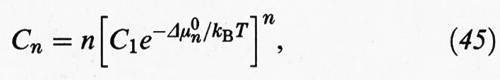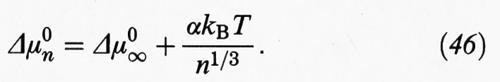Sistemi dispersi

Sistemi dispersi

SOMMARIO: 1. Introduzione. 2. Tipologia dei sistemi dispersi. 3. Struttura e dimensioni delle particelle. 4. Interfasi e interazioni fra le particelle. 5. Stabilità dei sistemi dispersi. 6. Fenomeni elettrocinetici.  7. Formazione dei sistemi dispersi.  8. Modelli per la descrizione dell'evoluzione nel tempo di un sistema di particelle.  9. Soluzioni micellari.  10. Aspetti applicativi.  11. Sintesi di materiali attraverso aerosol. 12. Dinamica dell'aerosol troposferico.  13. Conclusioni. □ Bibliografia.

1. Introduzione

Nel 1915 Wolfgang Ostwald - figlio del più noto Wilhelm, vincitore del premio Nobel per la chimica nel 1909 - definiva la scienza dei sistemi dispersi e dei colloidi il ‟mondo delle dimensioni dimenticate". Per diversi aspetti questa definizione si può ritenere tuttora valida, se si tiene conto dello scarso interesse che i sistemi dispersi suscitano in gran parte del mondo accademico. In realtà si tratta di una situazione curiosa, perché la conoscenza delle caratteristiche di tali sistemi ha un ruolo fondamentale nella descrizione di importanti fenomeni naturali e nello sviluppo di tecnologie avanzate volte alla preparazione di prodotti di largo consumo e di rilevanza sociale.

La caratteristica peculiare dei sistemi dispersi è rappresentata dal fatto di essere costituiti da una moltitudine di particelle, solide o liquide, disperse in un gas o in un liquido. Come illustrato nella fig. 1, si può immaginare un processo di suddivisione attraverso il quale si passi dalla materia massiva alle strutture laminari, quindi a quelle fibrillari e infine a quelle corpuscolari con un progressivo aumento della superficie. Gli atomi prossimi alla superficie si trovano in uno stato energetico diverso da quelli all'interno del solido, poiché le forze di interazione reciproca non risultano del tutto bilanciate. Essi presentano quindi una parziale saturazione dei legami possibili: tale saturazione si completa con molecole del fluido che vengono a contatto con il solido. Risulta allora opportuno esprimere l'energia totale E_t di un solido - data dalla somma dell'energia cinetica vibrazionale degli atomi e di quella potenziale dovuta alle loro interazioni - come somma di due contributi, dovuti rispettivamente all'energia interna E_i e all'energia superficiale E_s:

E_t = E_i + E_s = e_iV + e_sA. (1)

Nella (1) e_i indica l'energia interna per unità di volume ed e_s l'energia superficiale per unità di superficie, mentre V e A sono, rispettivamente, il volume e l'area della superficie del solido. Ne consegue:

I sistemi che verranno presi in considerazione sono quelli per i quali il rapporto (A/V) è dell'ordine di 10⁶ ÷ 10⁷ cm^-1. Poiché il secondo termine al secondo membro della (2) è molto più elevato del primo, esso assume un ruolo preponderante, conferendo particolare importanza all'energia superficiale. Le ricerche nel campo della chimica fisica dei sistemi dispersi sono quindi rivolte particolarmente allo studio delle caratteristiche delle superfici di contatto con l'ambiente circostante, dette interfasiche, in quanto ne condizionano profondamente il comportamento.

Un altro aspetto attentamente studiato è la stabilità delle dispersioni, sulla quale giocano un ruolo determinante le forze che agiscono fra le particelle, limitando eventuali processi di coagulazione o flocculazione.

Nello studio delle dispersioni è opportuno distinguere se si tratta di sostanze inorganiche, di soluzioni di polimeri o di altri composti organici. Di particolare interesse risultano quei sistemi in cui sono presenti molecole dette ‛anfifiliche', che - in virtù della loro peculiare struttura, in parte idrofila e in parte idrofoba - tendono a organizzarsi formando degli aggregati che vengono chiamati ‛micelle' (v. cap. 9).

Infine ricordiamo che la tendenza delle superfici a caricarsi positivamente o negativamente dà origine a peculiari fenomeni, detti ‛elettrocinetici' (v. cap. 6), quali ad esempio l'elettroforesi, un processo che consiste nel sottoporre una dispersione colloidale all'azione di un campo elettrico, la quale determina lo spostamento verso uno degli elettrodi delle particelle cariche. L'elettroforesi trova applicazione nell'identificazione e nella separazione delle macromolecole o di altre sostanze presenti nei colloidi.

2. Tipologia dei sistemi dispersi

I sistemi dispersi sono costituiti da particelle di piccole dimensioni (comprese fra 10^-8 e 10^-3 m), separate fra loro da un mezzo fluido. La loro classificazione è pertanto basata sia sulla natura e sulle proprietà dei liquidi o dei solidi che costituiscono la fase dispersa, sia sulle caratteristiche del mezzo disperdente. La situazione più comune è quella degli aerosol, nei quali dei solidi o dei liquidi sono dispersi in un gas. I fumi sono esempi del primo tipo, mentre le nebbie lo sono del secondo. Le dispersioni di gas in liquidi con elevata tensione superficiale danno origine anche alle schiume, mentre quelle di goccioline liquide, aventi dimensioni comprese fra un nanometro (nm) e un micron (µmm), in un altro liquido vengono chiamate emulsioni. In generale, i sistemi costituiti da piccole particelle o da macromolecole, di dimensioni comprese nell'intervallo ora menzionato, disciolte in un liquido vengono chiamati colloidi. Questo termine è stato impiegato per la prima volta da Thomas Graham nel 1861 per classificare le sostanze sulla base della loro velocità di diffusione nelle soluzioni e, soprattutto, della loro capacità di passare attraverso le membrane semipermeabili.

Le sostanze che diffondono rapidamente e che passano facilmente attraverso tali membrane sono state definite ‛cristalloidi', perché possono essere facilmente ottenute allo stato cristallino; viceversa le altre sostanze, quali le gelatine, che diffondono lentamente in soluzione e che non passano attraverso le membrane, sono state definite ‛colloidi' per il loro aspetto che richiama quello dei comuni adesivi liquidi. Peraltro molti di questi materiali non possono essere cristallizzati.

Questo criterio di classificazione, grazie anche al suo carattere operativo, si rivela del tutto appropriato, pur lasciando aperti molti problemi, connessi con la struttura e la stabilità delle dispersioni, la cui soluzione richiede ulteriori approfondimenti. Un altro criterio di classificazione dei sistemi dispersi è più specificamente legato alla loro stabilità. Per distinguere i colloidi dalle sospensioni macroscopiche essi vengono chiamati ‛sol', anche se si tratta di una distinzione non sempre soddisfacente. In particolari condizioni i sistemi colloidali possono manifestare le caratteristiche dello stato solido, poiché le molecole del solvente vengono intrappolate e, almeno parzialmente, immobilizzate in un reticolo in seguito alla formazione di legami chimici e fisici fra le molecole della fase dispersa. In questo stato vengono chiamati ‛gel'. La transizione da sol a gel può essere reversibile o irreversibile e dipende dalle sollecitazioni chimiche e fisiche cui viene sottoposta la dispersione. Gli aerosol sono però sempre irreversibili.

Sulla base dell'analisi precedente risulta allora possibile classificare i diversi tipi di sistemi dispersi secondo lo schema riportato nella tab. I. In tale quadro è opportuno soffermarci sulle polveri, secche o umide, che ci offrono un esempio tipico di sistema bifasico. Esse condividono coi fluidi la caratteristica di poter scorrere e hanno in comune con i gas la comprimibilità, mentre il loro comportamento macroscopico è controllato dalle interazioni fra le particelle, che danno luogo all'adesione e all'attrito.

L'impiego di sistemi di particelle solide in diverse produzioni manifatturiere e tecnologiche risale a tempi remoti. Gli antichi Egiziani impiegavano polveri inorganiche per fabbricare materiali ceramici e macinavano il grano per ridurlo in farina. La fabbricazione e il trattamento delle polveri hanno successivamente acquistato grande rilevanza con lo sviluppo delle tecnologie minerarie e metallurgiche.

Nel settore di indagine relativo ai sistemi dispersi confluiscono ricerche di tipo sia fondamentale che applicativo. Dal punto di vista metodologico, tali ricerche richiedono l'impiego di tecniche molto sofisticate, per lo più ottiche, per determinare le dimensioni, la distribuzione, la forma e la flessibilità delle particelle. L'analisi delle loro caratteristiche superficiali viene eseguita impiegando, oltre alla microscopia, l'adsorbimento di gas e la misura di campi elettrici superficiali. Lo studio delle interazioni fra le particelle e le molecole del solvente permette di individuare i fattori che determinano la stabilità delle dispersioni (v. cap. 5). Queste sono infatti intrinsecamente instabili dal punto di vista termodinamico, a causa dell'elevato valore della loro energia libera superficiale. La stabilità è dovuta a fattori cinetici, perché la repulsione fra le particelle limita in modo significativo la velocità dei processi di coagulazione.

L'applicazione di tali principî e metodologie trova ampio spazio nello studio di sistemi naturali quali le proteine, nella preparazione di prodotti di largo uso e nello sviluppo di moderne tecnologie industriali. Fra i prodotti rientrano i materiali polimerici, le gomme, le vernici, i detersivi, la carta, alcuni prodotti farmaceutici, alcuni materiali solidi impiegati in elettronica, alcuni prodotti alimentari e altri ancora. Fra i processi industriali la cui progettazione e gestione richiedono ampie conoscenze sui sistemi dispersi rientrano alcune tecnologie di separazione, la sintesi dei materiali polimerici, la separazione dei minerali per flottazione e altre tecniche.

Infine, la scienza dei sistemi dispersi interviene nelle ricerche sul comportamento dell'atmosfera, nella quale sono presenti diverse particelle solide o liquide che provengono da sorgenti naturali - marine, vulcaniche, ecc. - o da attività di origine antropica. La conoscenza e l'eventuale controllo dell'evoluzione e delle trasformazioni di tali particelle sono fondamentali per la protezione dell'ambiente.

3. Struttura e dimensioni delle particelle

La forma più semplice che si può attribuire alle particelle di un sistema disperso è ovviamente quella sferica. Molti sistemi colloidali, come ad esempio le emulsioni e gli aerosol liquidi, sono costituiti da particelle quasi sferiche. Anche le particelle cristalline sono spesso sufficientemente simmetriche da poter essere assimilate a sfere. Le molecole polimeriche e alcune proteine, a loro volta, si avvolgono su se stesse comportandosi talora come sfere. In realtà, le asimmetrie rispetto alla forma sferica costituiscono un fattore importante nel determinare le proprietà delle dispersioni, in particolare quelle meccaniche. La forma delle particelle è molto varia, ma in prima approssimazione esse possono essere classificate sulla base di semplici modelli geometrici, come quelli illustrati nella fig. 2.

Molte proteine hanno una forma che si approssima a quella di un ellissoide di rotazione, il quale, a seconda del rapporto esistente fra i semiassi a e b, viene detto ‛oblato' (a/b 〈 1) o ‛prolato' (a/b > 1). Le particelle di ossidi metallici e di argilla hanno una configurazione piatta a disco.

In generale, la caratterizzazione della morfologia delle particelle non è banale. Solitamente le loro dimensioni vengono determinate usando tecniche di classificazione meccanica mediante setacci, tecniche di sedimentazione, l'analisi microscopica, misure del campo elettrico superficiale e di dispersione della luce. Quest'ultimo approccio è quello che ha avuto maggiore sviluppo attraverso il trattamento delle immagini computerizzate, tecnica che si è rivelata particolarmente utile anche per interpretare la forma delle particelle mediante l'analisi di Fourier.

I materiali polimerici danno luogo a colloidi macromolecolari nei quali le lunghe molecole filiformi, con eventuali ramificazioni, sono disperse in un opportuno solvente. Ciò rende possibili le interazioni fra i diversi segmenti delle catene attraverso le forze di non legame, dette ‛di van der Waals', sia attraverso i legami a idrogeno, sia attraverso legami chimici covalenti veri e propri, che nell'insieme contribuiscono a modificare le proprietà meccaniche delle dispersioni. Tali molecole manifestano fra l'altro una notevole flessibilità dovuta alla rotazione attorno ai legami singoli, in particolare quelli fra due atomi di carbonio. Ne consegue che la loro forma è soggetta a un continuo cambiamento: pertanto gli studi teorici vengono spesso condotti assimilandole a corde avvolte su se stesse in modo casuale. La catena risulta costituita da una successione di legami, ciascuno dei quali è completamente libero di orientarsi nello spazio, indipendentemente dall'orientazione del suo predecessore, come illustrato nella fig. 3. Per facilitarne la descrizione matematica si assume, inoltre, che i diversi legami possano occupare la stessa posizione nello spazio. In tal caso, si dimostra che la probabilità w (r) che la distanza fra gli estremi della catena (v. fig. 3) sia uguale a r è espressa da:

dove N è il numero di legami, ciascuno di lunghezza b. In realtà, per una descrizione accurata è spesso necessario tenere conto del fatto che la presenza di interazioni fra diversi gruppi molecolari può impedire la libertà di rotazione attorno ai legami molecolari, limitando così la flessibilità.

I sistemi nei quali tutte le particelle hanno la stessa dimensione vengono detti ‛monodispersi'. Essi possono essere ottenuti solo con particolari accorgimenti e rivestono importanza per ben definite applicazioni. Solitamente si ha però a che fare con sistemi ‛polidispersi', nei quali le dimensioni delle diverse particelle differiscono e presentano una distribuzione il cui andamento, come vedremo, dipende dal modo in cui è stata preparata la dispersione stessa. Questo fatto influenza in modo significativo le loro proprietà e il loro comportamento.

4. Interfasi e interazioni fra le particelle

Come si è detto, una caratteristica essenziale e comune a tutti i sistemi dispersi è il valore particolarmente elevato del rapporto fra superficie e volume delle particelle. Ne consegue che i fenomeni caratteristici che si manifestano nelle regioni di separazione fra esse e il mezzo fluido disperdente, dette ‛interfasiche', acquistano particolare rilievo nel determinare la formazione, la stabilità e il comportamento di una dispersione. Pertanto, risulta di grande importanza conoscere le caratteristiche superficiali del materiale di cui è costituita la fase dispersa, che derivano, ad esempio, dall'eventuale accumulo di carica elettrica. Inoltre, sulla superficie di tale materiale si manifesta un accumulo delle diverse sostanze presenti nella fase fluida disperdente con la quale esso è a contatto. Questo fenomeno, chiamato ‛adsorbimento', è dovuto all'azione delle forze superficiali sulle molecole presenti nel gas o nel liquido, azione che induce le molecole ad accumularsi sulla superficie stessa, dove pertanto sono presenti in una concentrazione superiore a quella esistente nel cuore del fluido. Poiché l'adsorbimento di particolari molecole altera l'energia superficiale del solido, risulta allora possibile controllarne le proprietà modificando la natura delle sostanze adsorbite, in modo tale da influenzare il comportamento delle dispersioni stesse. Questo fatto ha ovviamente grande importanza nelle applicazioni.

I fenomeni superficiali, o interfacciali, vengono studiati mediante opportune tecniche sperimentali, come, ad esempio, la misura del potenziale elettrico superficiale. Altre misure riguardano il comportamento delle pellicole formate sulle superfici solide per l'adsorbimento delle molecole provenienti dalla fase fluida a contatto con le particelle solide. Il forte adsorbimento superficiale può dare luogo a strati monomolecolari e polimolecolari che talora possono essere assimilati a una pellicola liquida. Dal punto di vista energetico essi vengono caratterizzati dal valore della loro tensione superficiale - in un liquido espressa dalla forza per unità di lunghezza - che agisce sulla superficie perpendicolarmente a ogni linea giacente sulla superficie stessa. Operativamente essa è data dal rapporto fra il lavoro che deve essere compiuto per aumentare l'area della superficie e il corrispondente aumento che questa ha subito. Indichiamo con γ₀ il valore della tensione superficiale di una sostanza e con γ il valore che assume quando è adsorbita su una superficie solida. La differenza è dovuta all'effetto delle interazioni con la superficie. Si può allora definire una pressione superficiale, o di espansione (spreading), Π = c₀ - c, che risulta proporzionale al lavoro necessario per rimuovere la sostanza adsorbita dalla superficie.

La trattazione quantitativa dei fenomeni superficiali mediante la termodinamica soffre di un'incertezza connessa con la definizione della zona nella quale essi sono localizzati. Seguendo un approccio introdotto originariamente da J. W. Gibbs e successivamente modificato da altri autori, in particolare da E. A. Guggenheim, si assume che l'interfase che separa due fasi adiacenti α e β sia caratterizzata da un volume e da uno spessore finiti, come illustrato nella fig. 4; dal punto di vista termodinamico, essa viene trattata come una fase massiva nella quale però giocano un ruolo importante gli effetti dovuti all'energia interfacciale. Questo approccio, anche se non del tutto realistico, permette di descrivere quantitativamente i processi di adsorbimento. Operativamente ci si riferisce a una miscela fluida di diversi componenti a contatto con una superficie solida sulla quale essi vengono adsorbiti. Se n^σ_i è il numero di moli del componente i presente nella fase superficiale σ, la sua concentrazione superficiale è espressa dal rapporto Γ_i = (n^σ_i/), dove A è l'area della superficie stessa.

Per determinare lo stato termodinamico di uno strato di fluido adsorbito su una superficie è necessario impiegare ulteriori variabili indipendenti, oltre all'area A: precisamente l'entropia S^σ e il numero di moli dei diversi componenti adsorbiti. Questa impostazione consente di esprimere la variazione di energia della fase superficiale come somma di diversi contributi:

dE^σ = TdS^σ + γdA + Σ_im_idni^σ, (4)

in cui T è la temperatura assoluta e μ_i il potenziale chimico dell'i-esimo componente presente nella miscela fluida a contatto con il solido. Il primo termine al secondo membro esprime la variazione di energia dovuta agli scambi reversibili di energia termica con l'ambiente fluido, il secondo il contributo dovuto alla variazione della superficie e il terzo quello associato alla variazione del numero di moli dei diversi componenti adsorbiti sulla superficie. L'equazione precedente conferma che la tensione superficiale è espressa dalla derivata dell'energia interna rispetto alla superficie, tenendo costanti S^σ ed n^σ_i. La (4) è un'equazione differenziale omogenea, lineare rispetto alle variabili estensive presenti quali differenziali. In accordo con il teorema di Eulero, essa risulta compatibile con la seguente espressione differenziale, detta di Gibbs-Duhem:

che a temperatura costante porta alla seguente relazione:

Se l'adsorbimento avviene da una fase gassosa in cui è presente un solo componente, ne consegue che

dove R è la costante dei gas. Il termine all'ultimo membro esprime il differenziale del potenziale chimico in funzione della temperatura del sistema e della pressione P della fase gassosa. Pertanto, tenendo presente che dγ = - dΠ, si ottiene la relazione seguente:

nota come isoterma di Gibbs, che mette in relazione la pressione presente nella fase gassosa con la concentrazione superficiale Γ e la pressione superficiale Π. Essa ha avuto diverse conferme sperimentali dirette, attraverso la misura dei valori della concentrazione superficiale in funzione di P. I valori di Γ ottenuti sperimentalmente risultano in accordo con quelli calcolati mediante la (8), sulla base degli andamenti sperimentali di Π in funzione della pressione della fase gassosa.

Talora risulta possibile assimilare la fase adsorbita a un fluido bidimensionale il cui comportamento viene descritto mediante un'opportuna equazione di stato. Ad esempio, si può impiegare un'equazione di stato simile a quella di van der Waals (v. termodinamica molecolare, vol. XI), nella quale si assimilano le molecole a dischi rigidi non sovrapponibili, soggetti a una forza attrattiva che fornisce un legame fra Γ e Π. Se essa viene combinata con la (8) si ricava la seguente equazione, detta di Hill-De Boer,

in cui ϑ = C/C⁰ (dove Γ⁰ è la concentrazione corrispondente alla formazione di un monostrato) è il grado di ricoprimento della superficie, K è una costante che riflette le interazioni delle molecole adsorbite con il solido, e a è un parametro che riflette le interazioni attrattive fra le molecole stesse.

Nella fig. 5 vengono illustrati alcuni andamenti della (9) a varie temperature, come risulta dai dati sperimentali relativi all'adsorbimento del kripton sul bromuro di sodio. Si può osservare che alcune curve presentano un tratto quasi verticale corrispondente a una brusca variazione di ϑ in funzione di P. Questo fatto indica la presenza di una transizione di fase superficiale. Esiste una temperatura critica al di sopra della quale il processo non ha luogo.

5. Stabilità dei sistemi dispersi.

Per poter descrivere il comportamento di una dispersione è opportuno assimilare le particelle in essa presenti alle molecole di un fluido. Più propriamente essa viene assimilata a un ‛fluido sopramolecolare' le cui particelle sono soggette a moti browniani. Infatti le particelle con diametri inferiori a 5 µm sospese in un liquido manifestano caratteristici movimenti irregolari a zig-zag, dovuti agli urti non bilanciati con le molecole del mezzo disperdente. Questi movimenti, che possono essere osservati all'ultramicroscopio, sono stati individuati per la prima volta dal botanico Robert Brown nel 1827. L'interpretazione del fenomeno è stata data da William Ramsay nel 1876, mentre la sua descrizione quantitativa è stata formulata successivamente da M. Smoluchowski e A. Einstein agli inizi di questo secolo. In tale quadro le proprietà della dispersione si possono valutare applicando i metodi della termodinamica statistica e della teoria cinetica, attraverso la conoscenza delle leggi che esprimono l'interazione fra le particelle stesse (v. termodinamica molecolare, vol. XI).

Per approfondire l'importante argomento della stabilità delle dispersioni, in particolare dei sistemi colloidali, è anzitutto opportuno evidenziare che essa è essenzialmente dovuta all'adsorbimento di cationi o anioni provenienti dalla soluzione, che conferiscono una carica elettrica alla superficie delle particelle disperse. Un esempio ci viene offerto dalle particelle di silice disperse in acqua, che danno origine superficialmente ad acido silicico, il quale subisce a sua volta un'ulteriore dissociazione ionica:

SiO₂ + H₂O ⇌ SiO3^2- + 2H⁺.

Sulla superficie delle particelle vengono così segregate delle cariche negative che, a loro volta, esercitano un'azione attrattiva sugli idrogenioni presenti nella soluzione, con conseguente formazione di un doppio strato elettrico avente le caratteristiche illustrate nella fig. 6A. Esso è costituito da due regioni: quella interna, che include gli ioni adsorbiti sulla superficie, e quella diffusa, nella quale gli ioni presenti nella soluzione sono distribuiti secondo l'influenza delle interazioni elettrostatiche e dei movimenti termici casuali. In generale, quindi, l'adsorbimento di ioni inorganici od organici produce una barriera di energia elettrostatica che impedisce alle particelle di coagulare, con formazione di una fase precipitata, termodinamicamente più stabile.

Per descrivere in termini quantitativi i fenomeni precedenti è opportuno riferirsi, in prima approssimazione, a una superficie piana, trascurando la curvatura delle particelle, e simulare lo strato di ioni adsorbiti con una distribuzione di carica superficiale continua. Essa esercita sugli ioni di carica opposta presenti nella soluzione un'attrazione che tende ad accumularli in prossimità della superficie, alla quale si oppone l'agitazione termica che tende invece a distribuire in modo uniforme gli ioni nella soluzione. La loro distribuzione può allora essere espressa mediante la legge di Boltzmann:

C_i (r) = C_i (∞) exp (-z_iψ (r) e/k_BT), (10)

dove C_i (∞) è la concentrazione degli ioni nel cuore della soluzione (espressa in particelle/volume), ovvero a una distanza molto elevata dalla superficie della particella, z_i è la valenza degli ioni, ψ (r) l'energia potenziale a distanza r dalla superficie della particella, k_B è la costante di Boltzmann, e è la carica dell'elettrone e T è la temperatura assoluta.

Se si combina l'equazione precedente con quella di Poisson si ricava:

dove ε è la costante dielettrica del mezzo fluido. Per ottenere ψ (r) si deve risolvere l'equazione precedente utilizzando la condizione di elettroneutralità:

Si può ottenere una soluzione analitica semplice della (11) se si tiene conto che l'energia potenziale è piccola rispetto a quella termica, per cui zeψ (r)/k_B ≪ 1. Linearizzando il secondo membro e integrando si ricava:

ψ (r) = ψ⁰exp (-χr), (13)

essendo

e ψ₀ il valore del potenziale in corrispondenza della superficie.

In base alla (13) il potenziale decresce esponenzialmente; il termine 1/χ ha le dimensioni di una lunghezza, detta di Debye, e rappresenta lo spessore nel quale è essenzialmente localizzato il doppio strato elettrico superficiale.

I risultati precedenti possono essere applicati all'analisi della stabilità delle dispersioni colloidali, poiché la repulsione fra due particelle è dovuta all'interazione elettrostatica fra i loro doppi strati elettrici. Un modello per descrivere tale effetto è stato sviluppato da E. J. W. Verwey e J. Th. Overbeek e, indipendentemente, da B. Derjagin e L. D. Landau, per cui viene contraddistinto con l'acronimo DLVO.

Se le particelle sono sufficientemente grandi, il potenziale repulsivo può essere valutato utilizzando la (13), valida per due superfici parallele separate da una distanza 2 h. In tal caso si ottiene:

dove C è la concentrazione dell'elettrolita presente nella soluzione, mentre h è la distanza fra una superficie e il piano di simmetria, come illustrato nella fig. 6B. Infine, si ha:

Il potenziale di interazione espresso dalla (15) ha l'andamento riportato nella fig. 7A: si tratta di un potenziale a lungo raggio, molto sensibile agli elettroliti presenti nella soluzione.

Le particelle, inoltre, si attraggono reciprocamente per effetto di un potenziale V_A (h) dovuto alle interazioni di non legame determinate dalle forze di van der Waals, che si manifestano fra i diversi atomi presenti nelle particelle stesse. Tali interazioni, dette anche dispersive, risultano, secondo una classica trattazione sviluppata da F. W. London, inversamente proporzionali alla sesta potenza della distanza fra i due atomi considerati. Se si sommano tutte le interazioni attrattive che si manifestano fra gli atomi appartenenti a due particelle - riferendoci, sempre per semplicità, a superfici parallele - si ricava, assimilando il solido a un mezzo continuo e integrando, la seguente espressione:

il cui andamento è riportato nella fig. 7B. Anch'essa esprime un effetto a lungo raggio, insensibile, però, al contenuto di elettroliti. La costante A, detta di Hamaker, dipende dalla natura del materiale presente nelle particelle e ha un valore che si aggira intorno a 10^-20 ÷ 10^-19 J. In realtà la presenza di un mezzo disperdente, invece del vuoto, abbassa il valore dell'energia attrattiva che, pertanto, deve essere più propriamente calcolata con la seguente espressione:

dove gli indici 1 e 2 si riferiscono rispettivamente al mezzo disperdente e alle particelle. Globalmente il potenziale di interazione fra due particelle risulta allora descritto da una funzione data dalla somma di entrambi i contributi, attrattivo e repulsivo:

I segni presenti nei due addendi riflettono rispettivamente il ruolo repulsivo e attrattivo delle forze in gioco. L'andamento della (19) è rappresentato nella fig. 7C. L'energia presenta un massimo e quindi scende verso valori negativi che portano alla formazione di un agglomerato fra due particelle. Perché ciò avvenga è necessario superare una barriera di energia potenziale la cui entità dipende dal valore dei diversi parametri che compaiono nella (15) e che sinteticamente sono stati compendiati in B. Di particolare interesse è il ruolo del parametro χ che, in base alla (14), dipende dal prodotto fra la concentrazione degli ioni in soluzione e il quadrato della loro carica. Come illustrato nella fig. 8, all'aumentare di χ diminuisce l'altezza della barriera di potenziale e pertanto risulta agevolato il passaggio verso la configurazione più stabile che porta all'adesione fra le particelle.

Prima di procedere nell'analisi di stabilità va detto che sono stati effettuati anche calcoli volti a determinare la distribuzione spaziale delle particelle mediante il metodo Monte Carlo, seguendo la consueta impostazione della meccanica statistica (v. termodinamica molecolare, vol. XI). È stata così valutata la funzione di distribuzione radiale g (r): tale funzione, moltiplicata per il volume di un guscio sferico di spessore Δr e raggio r uguale alla distanza dal centro di una particella di riferimento scelta a caso e per la densità molecolare, fornisce il numero di particelle presenti nel guscio sferico stesso. Un esempio dei risultati ottenuti è illustrato nella fig. 9, relativa a un sistema di particelle con concentrazione uguale a 0,1 • 10^-3 moli/l. Le curve riportate nel diagramma si riferiscono a diversi valori delle frazioni volumetriche della dispersione. È interessante osservare che, quando la concentrazione volumetrica raggiunge valori relativamente elevati, la funzione di distribuzione radiale presenta dei massimi piuttosto netti, che indicano la presenza nel sistema di configurazioni regolari quasi cristalline. Configurazioni periodiche sono state individuate sperimentalmente, come illustrato nella fig. 10; esse si riscontrano in sedimenti di gel metallici, nella deposizione elettroforetica di sospensioni, in dispersioni di lattici polimerici e in altre situazioni analoghe. Il loro studio è interessante non solo dal punto di vista scientifico, ma anche perché le proprietà elastoplastiche che esse presentano risultano di particolare importanza in agricoltura e nell'industria.

Un'analisi della condizione di stabilità del sistema disperso può essere eseguita per via cinetica, valutando la velocità con la quale le particelle coagulano dopo aver subito una collisione. Tale velocità può essere determinata in base alla teoria formulata nel 1916 da M. Smoluchowski per interpretare l'evoluzione di una dispersione di particelle soggette a moti browniani. La velocità di coagulazione dipende, ovviamente, dalla concentrazione delle particelle e dall'intensità dei loro movimenti. Si procede allora valutando, in un sistema monodisperso, il flusso diffusivo delle particelle verso una di esse ed esprimendo, quindi, la diminuzione del loro numero come segue:

(N è la concentrazione delle particelle stesse). La costante k riflette la probabilità di avvicinamento di due particelle assimilate a sfere rigide che si muovono in un fluido continuo. In accordo con il menzionato lavoro di Einstein sui moti browniani, essa si può esprimere come segue:

dove μ è la viscosità del fluido.

La (20), che descrive la coagulazione attraverso un processo bimolecolare, può essere facilmente integrata con la condizione iniziale N = N⁰ a t = 0. Si ottiene la relazione seguente:

che descrive quantitativamente la diminuzione del numero di particelle libere al crescere del tempo.

In realtà la situazione precedente si riferisce a una rapida coagulazione, condizionata unicamente dal moto delle particelle nel fluido. La presenza della barriera di energia potenziale rappresentata nella fig. 7C rallenta tale processo di coagulazione, per cui la (20) deve essere più propriamente scritta come segue (H = 2h):

dove a è il raggio della particella. Se V = 0, l'espressione al denominatore risulta uguale a 1 e si recupera la coagulazione rapida. In presenza di una barriera energetica V è positivo e pertanto il valore di W risulta superiore all'unità. Di conseguenza la velocità di coagulazione diminuisce. In pratica il valore di W per molti sistemi colloidali è dell'ordine di 10⁷. In queste condizioni la coagulazione risulta trascurabile e il sistema appare stabile.

L'analisi precedente evidenzia che l'andamento della curva di energia potenziale e, soprattutto, l'altezza del suo massimo condizionano in modo significativo la probabilità di transizione verso la coagulazione del sistema disperso. Un altro punto importante è il ruolo esercitato dagli elettroliti che, come illustrato nella fig. 9, influenzano attraverso il parametro χ l'andamento della curva di energia potenziale. Si può dimostrare che l'inizio dell'instabilità è compatibile con le seguenti condizioni:

le cui caratteristiche sono illustrate nella fig. 11. Esse portano alla seguente espressione della concentrazione critica dell'elettrolita, C_crit, che dà luogo alla coagulazione:

Per bassi valori di ψ₀ (〈 25 mV) l'espressione precedente si può approssimare come segue:

Si osservi la forte dipendenza della concentrazione critica dalla valenza degli ioni che compare alla sesta potenza al denominatore. Ne consegue che la concentrazione di elettrolita richiesta per la coagulazione nel caso di ioni mono-, bi- e trivalenti sta nei rapporti 1: (1/2)⁶: (1/3)⁶ = 100 : 1,6 : 0,13. Questo risultato è in buon accordo con una regola empirica introdotta da Schulz e Hardy, basata sui risultati di una serie di esperimenti di coagulazione.

6. Fenomeni elettrocinetici.

I fenomeni elettrocinetici - scoperti dallo scienziato russo F. F. Reuss nel 1808 - riguardano il moto relativo di un sistema disperso rispetto a un fluido e sono rappresentati, in particolare, dall'elettroosmosi e dall'elettroforesi che, in un certo senso, si possono considerare complementari. Applicando una differenza di potenziale fra i due estremi di un mezzo poroso imbevuto d'acqua ha luogo un trasporto del liquido stesso nella direzione del polo negativo. Questo processo viene chiamato elettroosmosi. Se tale differenza di potenziale viene applicata a un recipiente contenente una dispersione solida in acqua (nell'esperienza originale si trattava di argilla), le particelle solide si muovono verso il polo positivo. Questo fenomeno di trasporto di una fase dispersa per effetto di un campo elettrico viene chiamato elettroforesi, e ha avuto molte applicazioni nella separazione selettiva dei diversi componenti che danno origine a una dispersione colloidale.

Nella seconda metà del secolo scorso, sono stati scoperti i processi opposti rispetto a quelli menzionati. Quando l'acqua viene filtrata attraverso una membrana porosa, o viene fatta fluire attraverso un singolo capillare, si manifesta una differenza di potenziale fra i punti estremi del mezzo, che viene chiamata ‛di corrente'. Se invece delle particelle di quarzo vengono lasciate cadere in acqua si riscontra, fra due elettrodi disposti a diversa altezza, una differenza di potenziale elettrico, chiamata ‛di sedimentazione'. I fenomeni descritti, essenzialmente dovuti alla presenza di cariche elettriche sulla superficie, sono schematizzati nella fig. 12. A titolo esemplificativo soffermeremo la nostra attenzione su uno di essi, l'elettroforesi. Il moto di una particella carica negativamente in un campo elettrico è illustrato nella fig. 13, dalla quale risulta che l'atmosfera ionica tende a muoversi in direzione opposta. In condizioni stazionarie la forza dovuta al campo elettrico è bilanciata dalle forze di attrito viscose, per cui la particella si muove con una velocità costante. Per calcolare tale velocità è necessario conoscere la distribuzione degli ioni attorno alla particella, che a sua volta dipende dal valore del potenziale ψ⁰ in corrispondenza delle superfici. Purtroppo ψ⁰ non risulta direttamente misurabile; viceversa è possibile misurare un'altra grandezza a esso vicina, chiamata ‛potenziale elettrocinetico' o ‛potenziale ζ', che rappresenta il valore del potenziale sulla superficie dove avviene la separazione fra la carica superficiale e la soluzione elettrolitica. La posizione esatta di tale superficie non è ben definita, poiché si riferisce in realtà alla regione nella quale si verifica un rapido cambiamento di viscosità.

La velocità della particella, u_p, risulta proporzionale all'intensità del campo elettrico X, attraverso la relazione approssimata u_p = εζX/πμ, essendo μ la viscosità. Mediante la sua applicazione risulta peraltro possibile valutare il potenziale ζ se si studia sperimentalmente il moto di una particella in un campo elettrico. Ad esempio, nel caso di dispersioni acquose ζ = 0,015 u_p/X, dove X è espresso in V/m e la velocità in m/s.

7. Formazione dei sistemi dispersi

La semplice macinazione di un materiale massivo non riesce in generale a produrre particelle di dimensioni così piccole da dare luogo a sistemi dispersi con le caratteristiche precedentemente discusse. Ciò soprattutto perché, prima o poi, nel corso della macinazione si raggiunge una situazione nella quale il processo di rottura viene bilanciato da quello di coagulazione dovuto alla forza attrattiva che si esercita fra le particelle.

Se si vogliono ottenere elevati gradi di dispersione, è allora opportuno procedere attraverso l'aggregazione di soluzioni molecolari soprasature che vengono fatte precipitare. Esistono diversi accorgimenti per conseguire tale risultato, quali la sostituzione di un buon solvente con uno meno buono, il raffreddamento o un'opportuna reazione chimica. Un esempio di queste reazioni è l'idrolisi del cloruro ferrico con acqua calda per formare il corrispondente ossido idrato:

FeCl₃ + H₂O (calda) → Fe₂O₃ (idrato).

In generale la formazione di una nuova fase durante tali precipitazioni coinvolge due stadi distinti, chiamati rispettivamente di ‛nucleazione' e di ‛crescita cristallina'. Le dimensioni e la distribuzione della dispersione così ottenuta sono essenzialmente condizionate dalla velocità relativa dei due processi: se la velocità di nucleazione è alta, in senso relativo, si ottiene un elevato grado di dispersione.

L'approccio più semplice alla descrizione dei processi di nucleazione, volto in particolare a stimare la velocità dei processi stessi e le dimensioni delle particelle che da essi si ottengono, è basato sulla cosiddetta ‛approssimazione capillare', nella quale si valuta l'energia libera di formazione dei nuclei di cristallizzazione attraverso le proprietà termodinamiche macroscopiche delle sostanze in esame. In particolare, la funzione energia libera di formazione di una particella, o goccia, sferica di raggio r da un vapore o da una soluzione soprasatura viene espressa come segue:

dove ΔG_v è la variazione di energia libera nel passaggio dalla fase gassosa a quella condensata o da una fase liquida a una fase solida, mentre σ è una grandezza caratteristica del solido preso in considerazione che esprime la sua energia per unità di superficie. Nel caso particolare in cui si consideri un processo di condensazione da una fase gassosa risulta che:

essendo P la pressione del gas, P⁰ la tensione di vapore della fase condensata e Ç il suo volume molare.

L'andamento della (27) è illustrato nella fig. 14, dove compare un massimo in corrispondenza di r*. Eguagliando a zero la derivata della (27) rispetto a r si ottiene:

essendo ΔG* la barriera di energia libera necessaria per la formazione dei nuclei critici che preludono alla formazione di particelle stabili. In base alle relazioni precedenti e impiegando i valori di σ dei comuni materiali si ottiene un valore del raggio r* molto piccolo, dell'ordine di 10 Å; compatibilmente con questo valore i nuclei contengono solo un centinaio di molecole. Questo risultato rivela un'inadeguatezza del modello descritto, dovuta essenzialmente all'impiego, in un calcolo condotto su particelle microscopiche, di una grandezza σ determinata con esperienze macroscopiche condotte su superfici piane, ignorando così l'influenza della curvatura delle particelle.

Sviluppando il modello, si ricava la seguente espressione della concentrazione dei nuclei critici con n* molecole:

C (n^*) = C(1) e^-ΔG*/kBT; (30)

C (1) è la concentrazione dei monomeri. La velocità di nucleazione I risulta allora espressa dal prodotto di tale concentrazione di equilibrio per la frequenza degli urti che i monomeri subiscono con i nuclei critici:

S (n*) = 4πr*² è l'area dei nuclei critici e β è la frequenza delle collisioni, che per un gas, in base alla teoria cinetica, si può esprimere nella forma:

dove m è la massa delle molecole.

La trattazione precedente costituisce in realtà solo un primo livello di approssimazione alla soluzione del problema in esame. Oltre a basarsi sul già menzionato impiego del parametro macroscopico σ, essa trascura anche gli effetti dovuti al depauperamento dei nuclei critici per effetto della loro crescita e alla rievaporazione delle molecole dai nuclei stessi. Per tenerne conto è stata formulata, da parte di diversi autori, una trattazione più accurata della cinetica della nucleazione, nella quale si assume che l'evoluzione dei nuclei proceda attraverso una successione di reazioni reversibili del tipo:

A₁ + A_n-1 A_n, (33)

essendo A₁ il monomero. Si tratta in sostanza di una successione di condensazioni ed evaporazioni di singole molecole. È allora opportuno indicare con f (n,t) l'effettiva concentrazione dei nuclei con n monomeri al tempo t, che differisce ovviamente dalla C (n) = C (1) exp (- ΔG⁰/k_BT), corrispondente alle condizioni di equilibrio. L'evoluzione del sistema può allora essere descritta mediante un approccio simile a quello che viene utilizzato per esprimere la diffusione in un sistema molecolare che non si trovi in condizioni di equilibrio. Il bilancio delle particelle risulta espresso dalla seguente equazione differenziale:

la quale, se si assimila βS (n) a un coefficiente di diffusione generalizzato, risulta simile alla seconda equazione di Fick della diffusione. Da essa si ottiene la seguente espressione della velocità di nucleazione:

I = βS(n^*)C(n^*)Z. (35)

Il termine Z, chiamato fattore di Zeldovitch, è a sua volta espresso dalla relazione:

Se si confronta la (35) con la (31) si può osservare che esse differiscono per il fattore Z, il cui valore è compreso fra 10^-1 e 10^-2, che riflette la natura diffusionale del processo di nucleazione.

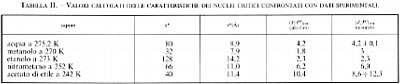
La (35) descrive soddisfacentemente la cosiddetta nucleazione omogenea, attraverso la quale si formano, per esempio, gocce di liquido da un vapore. Essa predice un netto aumento della velocità di nucleazione per un piccolo aumento della soprasaturazione, in accordo con i dati sperimentali. Ciò è confermato dai dati riportati nella tab. II, relativi a esperienze opportunamente condotte.

L'andamento della velocità di nucleazione in funzione della temperatura è illustrato nella fig. 15, dove è presente un massimo accentuato; ciò è dovuto al fatto che, all'aumentare della temperatura, in un primo tempo prevalgono gli effetti diffusivi, mentre successivamente prevalgono gli effetti dipendenti dalla concentrazione dei nuclei critici, la quale tende ad annullarsi in corrispondenza della temperatura di fusione.

8. Modelli per la descrizione dell'evoluzione nel tempo di un sistema di particelle

Un sistema di particelle può essere definito assegnando dei valori ad alcune caratteristiche delle particelle stesse, come le dimensioni, o ad alcune loro proprietà chimiche, come ad esempio la tendenza a partecipare a particolari reazioni chimiche o a favorirle. Nel caso di una dispersione, le caratteristiche dello sciame di particelle dovranno essere descritte mediante metodi statistici: ad esempio, si possono assumere come variabili caratteristiche la massa m delle particelle o il loro volume, che si ottiene direttamente dividendo m per la densità, posta costante. Le proprietà del sistema globale potranno allora essere descritte mediante una funzione di distribuzione f (m,t), tale che sia f (m,t) dm = numero di particelle presenti al tempo t, con massa compresa fra m ed m + dm. Solitamente tale funzione, come illustrato nella fig. 16, ha un valore nullo per m uguale a zero, passa per un massimo e tende quindi asintoticamente a zero. Esistono ovviamente casi di maggiore complessità, relativi ai cosiddetti sistemi polidispersi nei quali sono presenti più massimi. Se il sistema è soggetto a un'evoluzione, la funzione di distribuzione si trasforma nel tempo come indicato nella figura stessa. Inoltre valgono le seguenti relazioni di conservazione:

Il comportamento dinamico del sistema è descritto dalla seguente equazione differenziale, nota come ‛bilancio di popolazione' e indicata con l'acronimo PBE (Population Balance Equation):

dove g_m esprime la velocità di variazione della massa delle particelle per effetto sia della deposizione su di esse di alcuni componenti presenti nella fase fluida, che subiscono una eventuale trasformazione chimica, sia per evaporazione di molecole in essa presenti. I due termini B (birth) e D (death) esprimono invece la variazione, per unità di tempo e volume, del numero delle particelle aventi un ben definito valore della massa per effetto della coalescenza. La coalescenza, ovviamente, fa nascere particelle di una particolare massa m′, somma di quelle delle particelle che collidono, e fa morire le particelle di massa m che vengono catturate nelle collisioni che portano a coalescenza. I due termini in esame hanno, rispettivamente, la forma:

e

dove β (m, m′) è un coefficiente di coagulazione fra particelle di massa m ed m′. Infine I (m, t) è, al solito, la velocità di formazione delle particelle attraverso un processo di nucleazione.

Sostituendo le ultime espressioni nella (39) si ricava un'equazione integro-differenziale la quale richiama la nota equazione di Boltzmann che è alla base di tutta la teoria cinetica dei fluidi. Ciò contribuisce ulteriormente a giustificare la menzionata analogia fra un gas e un sistema disperso che, come abbiamo visto, può essere assimilato a un fluido sopramolecolare. La (39) è di grande importanza, poiché descrive l'evoluzione dinamica di un sistema di particelle; la sua integrazione può essere in generale eseguita o per simulazione, con il metodo Monte Carlo, o mediante metodi numerici approssimati, come quello dei momenti. Ovviamente tale risultato può essere raggiunto solo se si conoscono espressioni specifiche delle funzioni I, g_m e β, che riflettono rispettivamente i fenomeni di nucleazione, crescita e coagulazione delle particelle e che costituiscono gli inalienabili ingredienti fisici del processo che si sta esaminando.

9. Soluzioni micellari

Fra i sistemi dispersi rivestono particolare importanza le soluzioni acquose di sostanze costituite da molecole chiamate ‛anfifiliche'. La loro caratteristica è di avere una lunga coda ‛idrofoba', come ad esempio una catena idrocarburica, e una testa ‛idrofila', costituita ad esempio da un residuo che dà origine a una dissociazione ionica. Esempi di molecole anfifiliche sono i sali alcalini degli acidi grassi, quali l'oleato di sodio, C₁₇H₃₃COONa, gli alchilsolfonati alcalini e così via. Questi composti agiscono quali tensioattivi perché diminuiscono la tensione superficiale dell'acqua e quindi vengono impiegati come detersivi.

La caratteristica peculiare delle molecole anfifiliche è quella di dare origine ad aggregati molecolari aventi molteplici strutture che sono tuttora oggetto di ampie indagini. Nella soluzione di un tensioattivo esiste una notevole varietà di strutture che vanno dalle micelle sferiche a quelle cilindriche, a quelle lamellari, alle micelle inverse, alle microemulsioni (v. fig. 17). L'importanza dello studio dei sistemi anfifilici è duplice, poiché essi da un lato, in quanto sistemi molecolari che si autoorganizzano, possono costituire dei modelli delle strutture presenti negli organismi viventi, quali le membrane lipidiche, e dall'altro trovano importanti applicazioni in diversi settori. Le ricerche in corso riguardano la sintesi di nuovi tensioattivi e lo studio del rapporto che intercorre fra la struttura delle molecole e il loro comportamento termodinamico e cinetico.

Soffermiamo la nostra attenzione sulle micelle sferiche, la cui struttura è illustrata nella fig. 18 per il caso specifico del dodecilsolfonato. Le micelle hanno un cuore idrocarburico idrofobo e un guscio idrofilo sul quale sono localizzati i residui ionici. Questi sistemi micellari presentano due caratteristiche essenziali: 1) se si aumenta gradualmente la concentrazione di un tensioattivo in una soluzione acquosa, le micelle compaiono solo se si raggiunge un valore ben definito di tale concentrazione, detta ‛concentrazione critica micellare' (CMC, Critical Micellar Concentration); 2) al di sopra della CMC la concentrazione del monomero in soluzione resta costante o aumenta solo lentamente. Per interpretare tale comportamento è opportuno descrivere l'equilibrio di aggregazione come segue:

nS ⇌ S_n,  n = 2, 3, ..., (42)

avendo indicato con S una delle molecole di tensioattivo e con S_n una micella formata da n di tali molecole. In condizioni di equilibrio termodinamico:

essendo rispettivamente N_n il numero di aggregati costituiti da n monomeri e N il numero di monomeri presenti nella soluzione. Inoltre:

dove N_H2O è invece il numero di molecole d'acqua. Infine K è la costante di equilibrio e ΔG0_n la variazione di energia libera standard associata alla formazione di una micella da n molecole di monomeri. Risolvendo il sistema di equazioni algebriche precedenti si possono valutare i diversi N_n, purché si conoscano i valori di ΔG0_n, ovvero delle variazioni di energia libera associate alla condensazione di n monomeri per formare il corrispondente aggregato.

In ΔG0_n sono presenti due contributi in competizione fra loro: il primo è indipendente dalle dimensioni delle micelle e deriva dalla tendenza verso la transizione di fase indotta dall'insolubilità della parte idrocarburica delle molecole; il secondo dipende invece dalle dimensioni delle micelle e riflette le interazioni repulsive fra le teste idrofile delle molecole anfifiliche, che sono essenzialmente localizzate nel guscio sferico superficiale della micella. Sviluppando tale approccio si ricava la seguente espressione approssimata della concentrazione degli aggregati micellari:

essendo C_n la concentrazione di aggregati con n monomeri e C₁ la concentrazione dei monomeri. Δμ0_n rappresenta la variazione di energia libera di un monomero nel passaggio dalla soluzione a un aggregato costituito da n unità, che a sua volta si può esprimere come somma di due contributi:

Il primo di essi, Δμ0_∞, rappresenta la variazione di energia libera, sempre per monomero, nel passaggio dalla soluzione a un aggregato di dimensioni infinite; il secondo riflette invece l'influenza delle dimensioni degli aggregati, attraverso le interazioni che si manifestano fra i residui ionici dei monomeri che tendono a localizzarsi sulla superficie degli aggregati; α è una costante caratteristica che rappresenta l'influenza di tali interazioni.

Se si riporta su un diagramma l'andamento della concentrazione del monomero presente in una soluzione e quella di un aggregato con n molecole anfifiliche in funzione di N si ottengono le curve illustrate nella fig. 19. Il loro andamento giustifica il concetto di concentrazione critica micellare, poiché solo al di sopra della CMC compare l'aggregato, mentre la concentrazione del monomero si mantiene costante.

10. Aspetti applicativi

Nei capitoli precedenti è stata presentata una panoramica dei principali aspetti che caratterizzano la scienza dei sistemi dispersi e delle interfasi, che, come abbiamo visto, tendono a convergere in un'unica disciplina. I punti qualificanti si riscontrano nello studio della struttura, della stabilità e dell'evoluzione di tali sistemi, a partire dalle informazioni microscopiche sulle interazioni molecolari.

La fig. 20 riassume in forma schematica le informazioni e i concetti discussi in precedenza, indicando i diversi settori nei quali sono utilizzati e in che modo questi si interconnettano. Come si è già detto (v. cap. 2), i settori applicativi per i quali si richiedono le competenze richiamate nella figura riguardano sia numerosi prodotti costituiti da una dispersione colloidale (aerosol, materiali compositi, prodotti alimentari, additivi per oli, vernici, farmaci, ecc.) o da una soluzione di un tensioattivo (detersivi, erbicidi, insetticidi, ecc.), sia processi che fanno uso di tensioattivi o di altri fenomeni correlati ai sistemi dispersi (flottazione, trattamento delle acque, flocculazione selettiva, recupero assistito del petrolio, interventi per la tutela ambientale, analisi chimica e fisica dell'atmosfera, ecc.).

Sotto il profilo ingegneristico, i settori precedenti contemplano l'applicazione delle tecnologie dei sistemi multifasici finemente suddivisi, quali le polveri fini, le micelle, le microemulsioni, gli aerosol, i film sottili, le fibre, le schiume, le strutture porose, le superfici irregolari e le macromolecole. Molti dei fattori importanti in tali sistemi ‛microeterogenei' hanno ricadute anche sull'ingegneria delle reazioni chimiche; altri possiedono alcune proprietà tipiche dei sistemi colloidali e devono essere ancora esplorati a fondo. Quest'ultimo è il caso, per esempio, dei semiconduttori costituiti da particelle colloidali che, in virtù delle loro dimensioni, presentano dei tipici effetti quantistici potenzialmente di notevole interesse applicativo. Le loro proprietà ottiche ed elettroniche risultano peraltro più legate alla struttura delle molecole di cui sono costituiti che alle proprietà del materiale solido. Un esempio ci viene offerto dal fosfuro di cadmio, che in forma massiva si presenta come un solido nero, ma che può assumere un'ampia gamma di colorazioni se viene disperso in particelle con diametri compresi fra 2 e 10 nm. Inoltre, queste particelle sono in grado di promuovere effetti fotocatalitici che possono essere opportunamente modulati variando le dimensioni delle particelle stesse.

L'esame di tutti i settori menzionati risulterebbe troppo ampio e specialistico. A titolo esemplificativo ne approfondiremo solo alcuni, che riguardano in particolare la sintesi dei materiali avanzati e la chimica atmosferica, evidenziandone le strette connessioni con le informazioni e i concetti discussi nei capitoli precedenti.

11. Sintesi di materiali attraverso aerosol

La sintesi di alcuni materiali inorganici impiegati in tecnologie avanzate viene attualmente effettuata in reattori nei quali si ottiene un aerosol di particelle ultrafini di elevata purezza e di dimensioni appropriate per le applicazioni previste. Quali esempi si possono citare i biossidi di titanio e silicio, diversi carburi, boruri e azoturi. Le polveri ultrafini così ottenute possono essere direttamente utilizzate per la fabbricazione di manufatti o sottoposte a ulteriori reazioni.

La tecnica impiegata per la loro sintesi consiste in un rapido riscaldamento, associato a una reazione chimica che ha luogo in fase vapore, con formazione di uno sciame di particelle diluito in una fase gassosa che lo trasporta verso uno stadio di separazione. Così si prepara, ad esempio, il biossido di silicio SiO₂, che viene ottenuto, a partire da tetracloruro di silicio, iniettando il reagente in una fiamma formata bruciando una miscela di idrogeno e ossigeno. Hanno luogo le seguenti reazioni:

SiCl₄ + O₂ → SiO₂+2Cl₂

SiCl₄ + 2H₂O → SiO₂+4HCl.

Il processo avviene in un reattore operante a 1.700 °C; in sostanza hanno luogo delle reazioni pirolitiche che producono molecole di SiO₂, le quali successivamente danno origine a una dispersione di particelle attraverso processi di nucleazione e crescita come quelli precedentemente descritti. Le particelle di silice così ottenute possono essere fuse per produrre vetri sintetici, impiegati per la fabbricazione di fibre ottiche. Alternativamente possono essere fatte reagire con carbone suddiviso, riscaldando una miscela dei due precursori in atmosfera di azoto a 1.800 °C. La reazione, agevolata dall'elevata superficie specifica dei materiali impiegati come reagenti, dà origine a una polvere di carburo di silicio (β-SiC), costituita da particelle aventi un diametro medio di circa 0,1 µmm, dalla quale per sinterizzazione si ottengono materiali utilizzati quali refrattari.

Un processo analogo può essere impiegato per produrre, ad esempio, carburo di boro, B₄C, partendo dall'ossido ottenuto in un reattore ad aerosol attraverso la reazione: 7C + 2B₂O₃ ⇌ B₄C + 6CO, che solitamente avviene riscaldando in un arco elettrico ossido di boro e carbonio massivi. Si tratta di una reazione molto lenta che richiede diversi giorni per essere completata a causa della difficoltà di sottrarre calore alla miscela reagente. Il processo risulta invece molto rapido se viene condotto riscaldando una miscela di B₂O₃ e carbone in polvere, preparati entrambi in opportuni reattori ad aerosol. Questo approccio permette di ottenere materiali più pregiati, perché più uniformi e quindi caratterizzati da una più elevata durezza, con un minore dispendio di energia.

12. Dinamica dell'aerosol troposferico

La troposfera, la parte più bassa dell'atmosfera, si eleva a 10 ÷ 15 km di altezza dal suolo; in essa, che include più dell'80% della massa atmosferica, si svolgono gran parte dei fenomeni meteorologici che riguardano il nostro pianeta. Nella troposfera sono presenti particelle provenienti da diverse sorgenti naturali, quali le polveri trascinate dai venti, gli spruzzi marini, le emissioni dei vulcani e particelle di origine antropica, come ad esempio quelle derivanti dalla combustione. Solitamente si distingue fra un aerosol primario, costituito dalle particelle che vengono rimosse dal suolo e trasportate nell'atmosfera, e uno secondario, costituito da quelle che si formano attraverso le trasformazioni chimiche che avvengono nell'ambiente stesso. Le dimensioni e la composizione delle particelle possono cambiare per coagulazione con altre particelle, per reazioni chimiche o per condensazione dell'acqua che le trasforma in nebbia o gocce liquide. Le particelle vengono successivamente rimosse dall'atmosfera attraverso due meccanismi: il primo è costituito dalla deposizione sulla superficie terrestre, mentre il secondo è dovuto alla cattura da parte di gocce liquide durante le precipitazioni.

L'aerosol atmosferico influisce in modo significativo anche sulla radiazione solare, una parte della quale viene direttamente diffusa o assorbita, influenzando, a sua volta, la formazione delle nuvole, poiché favorisce la condensazione del vapor d'acqua sulle particelle stesse.

L'insieme di questi fenomeni sottolinea l'importanza di simulare e, al limite, prevedere il comportamento delle dispersioni atmosferiche, approfondendo le interazioni fra i processi chimici e fisici in esso coinvolti e tenendo opportunamente conto degli effetti dovuti alle attività umane. Si tratta ovviamente di un problema di grande rilevanza, ma anche di grande difficoltà, poiché comporta la previsione delle dimensioni, della composizione, delle proprietà igroscopiche e della capacità di diffondere e assorbire le radiazioni elettromagnetiche delle particelle che costituiscono l'aerosol atmosferico. Le specie che maggiormente influenzano la sua composizione sono l'acido solforico (H₂SO₄), l'acido nitrico (HNO₃), l'acido cloridrico (HCl), l'ammoniaca (NH₃) e una serie di composti organici contenenti più di 5 atomi di carbonio per molecola. Questi composti possono essere considerati i precursori di un'ampia e complessa serie di reazioni chimiche che contribuiscono alla formazione e all'evoluzione delle particelle stesse. Anche se la descrizione dettagliata dell'aerosol atmosferico esula dai nostri scopi (v. atmosfera, chimica della, vol. X) riteniamo interessante riassumerne alcune caratteristiche essenziali nella fig. 21.

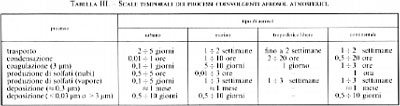
I modelli matematici che vengono impiegati per comprendere e descrivere l'evoluzione dinamica dell'aerosol atmosferico derivano dall'impostazione che ha portato all'equazione (39). Si tratta di un settore di ricerca ancora in fase di sviluppo, data la complessità e la molteplicità dei fenomeni coinvolti e delle scale spaziali su cui vanno considerati, che variano da quella urbana a quella planetaria; inoltre, poiché sono fenomeni molto diversificati, coinvolgenti il trasporto o le trasformazioni delle particelle, essi avvengono su scale temporali molto diverse (v. tab. III). In conseguenza di ciò risulta opportuno formulare equazioni di bilancio diverse a seconda delle diverse scale spaziali e temporali, così che esse costituiscano, in un certo senso, le tessere di un ampio mosaico in grado di fornire la simulazione globale del sistema preso in considerazione.

13. Conclusioni

La rassegna presentata nei capitoli precedenti prende in esame diversi aspetti della sempre più vasta scienza dei sistemi dispersi. Questa coinvolge metodologie sperimentali sofisticate e fa ampio uso di concetti e teorie di origine diversa. Inoltre, riveste un ruolo rilevante in altre discipline scientifiche e ha importanti ricadute economiche, come è stato più volte evidenziato ed esemplificato. La sua rilevanza nella biologia è stata sottolineata da un'affermazione dello scienziato russo I. L. Zhubov, secondo il quale: ‟Un essere umano è un colloide che cammina".

Lo studio dei sistemi dispersi interviene in modo determinante anche nella soluzione dei problemi connessi con la protezione dell'ambiente. Malgrado ciò, purtroppo si tratta di uno studio non sufficientemente coltivato, sia per quanto riguarda la ricerca che nell'ambito dell'insegnamento. Questa situazione appare poco comprensibile, soprattutto se si tiene conto che la natura interdisciplinare della scienza in questione si presta in modo particolare all'educazione dei giovani, in quanto porta a interagire cultori di diverse discipline e ad affrontare problemi atipici.

BIBLIOGRAFIA

Boer, J. H. de, The dynamical character of adsorption, Oxford 1968².

Carrà, S., Struttura e stabilità: introduzione alla termodinamica dei materiali, Milano 1978.

Carrà, S., Chimica fisica dei sistemi dispersi, in ‟La chimica e l'industria", 1986, LXVIII, 3, pp. 61-71.

Carrà, S., Morbidelli, M., Storti, G., Role of surfactants in emulsion polymerization, in Physics of amphiphiles: micelles, vesicles and microemulsions (a cura di V. Degiorgio e M. Corti), Amsterdam-New York 1985, pp. 483-512.

Dewey Carpenter, K., Colloids, in Encyclopedia of polymer science and technology: plastics, resins, rubbers, fibers (a cura di H. F. Mark e altri), vol. III, New York 1966, pp. 16-73.

Fan, L.-S., Rathman, J. F., Ghosh-Dastidar, A., Weimer, A. W., Kimura, S., Particle technology: the potential of reaction engineering, in ‟Chemical engineering progress", 1994, XC, 4, pp. 55-64.

Flory, P. J., Principles of polymer chemistry, Ithaca, N. Y., 1953.

Fridrikhsberg, D. A., Kurs kolloidnoi khimii, Moskva 1974 (tr. ingl.: A course in colloid chemistry, Moscow 1986).

Israelachvili, J. N., Thermodynamics and geometric aspects of amphiphile aggregation into micelles, vesicles and bilayers, and interactions between them, in Physics of amphiphiles: micelles, vesicles and microemulsions (a cura di V. Degiorgio e M. Corti), Amsterdam-New York 1985, pp. 24-58.

Matjevich, E., (a cura di), Surface and colloid science, 13 voll., New York 1969-1984.

Ostwald, W., Die Welt der vernachlässigten Dimensionen, Dresden-Leipzig 1915.

Pandis, S. N., Wexler, A. S., Seinfeld, J., Dynamics of tropospheric aerosol, in ‟Journal of physical chemistry", 1995, XCIX, pp. 9646-9659.

Pound, G. M., Nishioka, K., Lothe, J., Theory of homogeneous nucleation from the vapour, in Surface chemistry and colloids (a cura di M. Kerker), London 1972, pp. 147-188.

Shaw, D. J., Introduction to colloid and surface chemistry, London 1970².

Vold, R. D., Vold, M. J., Colloid and interface chemistry, Reading, Mass., 1983.

Voyutsky, S. S., Colloid chemistry, Moscow 1978.