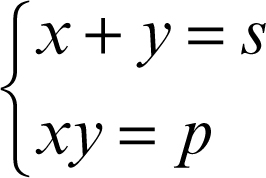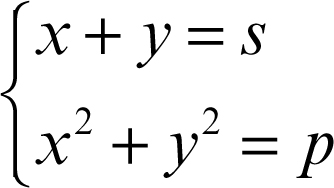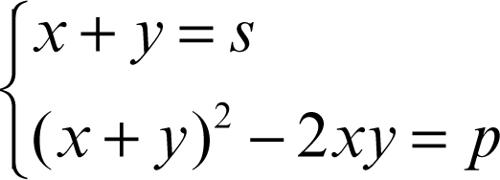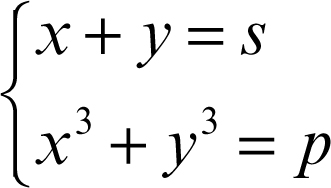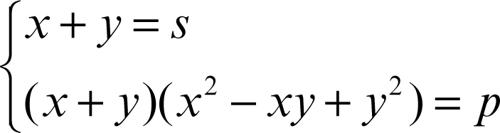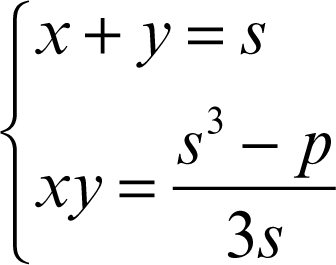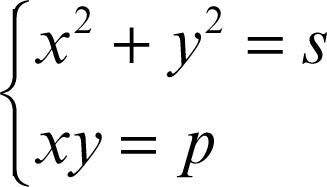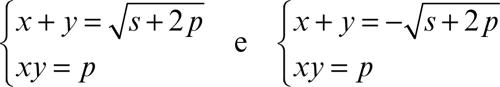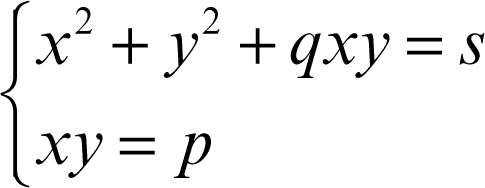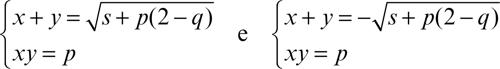sistema simmetrico
sistema simmetrico
sistema simmetrico sistema di due equazioni in due incognite x e y invariante rispetto allo scambio delle due incognite. In un sistema simmetrico a coefficienti reali la simmetria del sistema è equivalente al fatto che le due curve rappresentate dalle equazioni del sistema siano simmetriche rispetto alla retta di equazione y = x, bisettrice del primo e del terzo quadrante nel piano cartesiano. È possibile ricondursi, mediante trasformazioni algebriche, ad alcuni casi tipici per i sistemi simmetrici di secondo, terzo e quarto grado.
Sistemi simmetrici di secondo grado
Nei sistemi della forma
le relazioni che legano la somma e il prodotto delle soluzioni di un’equazione di secondo grado ai coefficienti dell’equazione stessa conducono a risolvere l’equazione (nella nuova incognita z):
Se z1 e z2 sono le soluzioni di tale equazione, allora le soluzioni (eventualmente complesse) del sistema di partenza sono le due coppie (z1, z2) e (z2, z1).
Un sistema della forma
può essere riscritto come
Sostituendo s al posto di x + y nella seconda equazione, ci si riconduce a un sistema simmetrico del precedente tipo.
Sistemi simmetrici di terzo grado
Un sistema della forma
può essere riscritto come
Supponendo s ≠ 0 (perché altrimenti la seconda equazione è ininfluente), il sistema è equivalente al sistema
Ci si riconduce quindi a un sistema simmetrico di secondo grado.
Sistemi simmetrici di quarto grado
Un sistema della forma
si spezza nei due sistemi simmetrici di secondo grado già esaminati:
Un sistema della forma
si spezza nei due sistemi simmetrici di secondo grado già esaminati:
