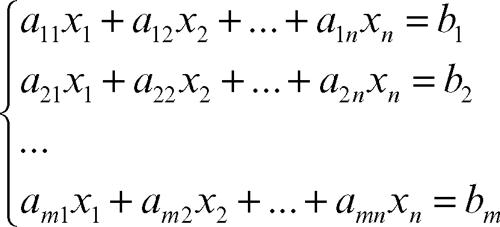sistema lineare
sistema lineare
sistema lineare sistema di equazioni algebriche di primo grado, vale a dire riconducibile a un sistema della forma
detta forma canonica di un sistema lineare, dove x1, x2, …, xn sono le incognite del sistema e dove gli aij e i bi (i = 1, …, m; j = 1, …, n) sono numeri reali (o complessi) dati. Un sistema lineare può essere sempre scritto in modo compatto nella forma matriciale (→ matrice) Ax = b, dove
sono rispettivamente una matrice m × n, detta matrice dei coefficienti del sistema, un vettore colonna n-dimensionale, detto vettore delle incognite del sistema, e un vettore colonna m-dimensionale, detto vettore dei termini noti del sistema. Se il vettore dei termini noti è nullo, allora il sistema lineare è detto sistema omogeneo. Un sistema omogeneo possiede sempre la soluzione banale, formata da tutti 0; ogni altra soluzione del sistema diversa da quella banale è detta autosoluzione. Un sistema omogeneo ammette autosoluzioni se e solo se il rango della matrice dei coefficienti A è minore del numero delle incognite (vale a dire del numero delle colonne di A). Soluzione del sistema è ogni n-pla ordinata di numeri reali (o complessi) che verificano tutte le equazioni assegnate; un sistema lineare che ammetta soluzioni è detto compatibile. Per il teorema di → Rouché-Capelli, un sistema della forma Ax = b è compatibile se e solo se la matrice A ha lo stesso rango della matrice m × (n + 1) ottenuta aggiungendo ad A il vettore colonna b.
Geometricamente, assegnare un’equazione lineare in n incognite equivale ad assegnare un sottospazio affine di codimensione 1 dello spazio affine An. Risolvere un sistema di m equazioni lineari in n incognite equivale pertanto a determinare l’intersezione di m sottospazi affini di An: se per esempio n = 2, allora si tratta di determinare l’intersezione di m rette nel piano affine A2, se invece n = 3, allora si tratta di determinare l’intersezione di m piani nello spazio affine A3. L’insieme delle soluzioni di un sistema lineare può ridursi all’insieme vuoto (come per esempio nel caso di due piani paralleli in A3, cioè di due equazioni che differiscono per il solo termine noto), a un solo punto (come per esempio nel caso di due rette non parallele in A2) oppure consistere di un numero infinito di punti, i quali formano un sottospazio dello spazio affine (come per esempio nel caso di due piani non paralleli in A3, che individuano gli infiniti punti di una retta). Nel caso di un sistema compatibile in n incognite, se il sottospazio affine di An formato dalle sue soluzioni è una retta (vale a dire se esso è un sottospazio affine di dimensione 1) si scriverà che il sistema ha ∞1 soluzioni, se esso è un piano (vale a dire se esso è un sottospazio affine di dimensione 2) si scriverà che il sistema ha ∞2 soluzioni, se esso è un sottospazio affine di dimensione k si scriverà che il sistema ha ∞k soluzioni.
Dato un sistema lineare compatibile, se il rango della matrice dei coefficienti A è inferiore al numero delle incognite n (vale a dire al numero delle colonne di A), allora il sistema ammette infinite soluzioni; se invece il rango di A è uguale a n, allora il sistema è equivalente a un sistema quadrato di ordine n (ottenibile selezionando un qualsiasi sottosistema di n equazioni indipendenti dal sistema di partenza) e ammette un’unica soluzione, che può essere calcolata mediante la regola di Cramer (→ Cramer, metodo di). Tale regola si basa sul calcolo di n + 1 determinanti di ordine n e il suo impiego richiede una mole proibitiva di calcoli già per “piccoli” valori di n (è infatti necessario effettuare un numero di operazioni dell’ordine di n!); il suo uso viene dunque solitamente evitato mediante il ricorso a metodi di calcolo numerico: i più usati si fondano sulla decomposizione della matrice A in fattori triangolari (→ matrice, decomposizione di una; → Gauss-Seidel, metodo di) a partire dai quali si può ricavare l’unica soluzione del sistema con un costo dell’ordine di n3 operazioni. Particolare importanza, ai fini dell’impiego di tecniche numeriche e della valutazione dei risultati, ha l’esame dell’indice di condizionamento della matrice A, definito come il numero reale positivo k(A) = ‖A‖ ⋅ ‖A−1‖, dove A−1 indica l’inversa di A e ‖…‖ indica la norma di una matrice: tale numero indica la sensibilità della soluzione rispetto a “errori” inerenti ai dati oppure dovuti al procedere dei calcoli. La particolare struttura della matrice A può suggerire l’impiego di algoritmi appositi; nel caso di sistemi di grandi dimensioni trovano impiego soprattutto metodi iterativi (→ Jacobi, metodo di; → Gauss-Seidel, metodo di).