riferimento, sistema di
riferimento, sistema di
riferimento, sistema di in termini generali, insieme di oggetti geometrici e algebrici e di procedure che consente di individuare la posizione di un punto di uno spazio metrico e di caratterizzare mediante equazioni luoghi geometrici di punti dello spazio. A seconda dello spazio ambiente si può avere un sistema di riferimento euclideo, affine, proiettivo. Un sistema di riferimento può essere definito anche localmente, per esempio nell’intorno di un punto di una superficie. Ulteriori esempi di sistemi di riferimento sono l’ascissa curvilinea di un punto su un arco di curva e il reticolato meridiani-paralleli su una superficie sferica (→ coordinate geografiche). La scelta di un particolare sistema di riferimento è dovuta a ragioni di semplicità; così, per esempio, un sistema di riferimento polare è preferibile per rappresentare una spirale, mentre un sistema di riferimento cartesiano è preferibile per rappresentare una retta o una conica.
Sistema di riferimento in una retta
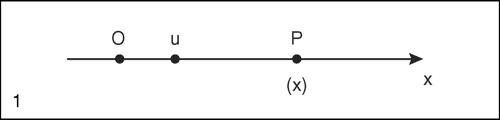
Introdurre un sistema di riferimento su una retta r vuol dire fissare su di essa un punto O, detto origine, un verso e un’unita di misura u. In tal modo a ogni punto P ∈ r è associato un numero reale x, detto ascissa del punto P, dato dalla misura con segno del segmento orientato OP, rispetto all’unità di misura u. La corrispondenza che si stabilisce tra punti di r e numeri reali è una corrispondenza biunivoca (→ Cantor-Dedekind, assioma di).
Sistema di riferimento cartesiano in un piano
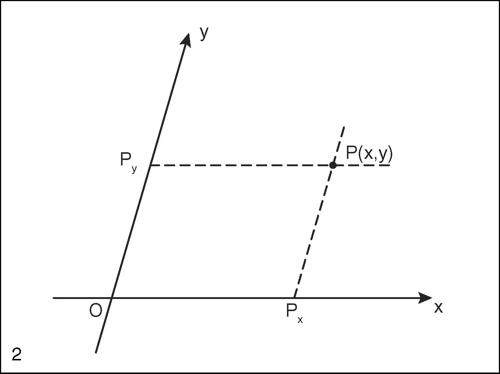
La procedura può essere estesa al piano, fissando su di esso una coppia di rette, dotate ognuna di un sistema di riferimento e aventi in comune il punto origine O. A ogni punto P del piano è associata, in modo biunivoco, la coppia ordinata di numeri reali (x, y), costituita dalle misure con segno dei segmenti orientati OPx e OPy, dove Px e Py indicano, rispettivamente, le proiezioni di P parallele alle rette prefissate sulle rette stesse. Il punto O è detto origine, le rette prefissate assi cartesiani (asse x o asse delle ascisse e asse y o asse delle ordinate), i numeri della coppia ordinata (x, y) sono detti coordinate di P (rispettivamente ascissa la x, ordinata la y). Un sistema di riferimento così definito è detto sistema di riferimento cartesiano. Se gli assi sono perpendicolari si ha un sistema di riferimento cartesiano ortogonale; se in più le unità di misura sui due assi sono uguali il riferimento è monometrico.
Sistema di riferimento in uno spazio di dimensione n ≥ 3
Più in generale è possibile introdurre un sistema di riferimento cartesiano in un qualsiasi spazio di dimensione n ≥ 3, fissando n distinte rette orientate, dette assi, concorrenti in uno stesso punto origine O, a tre a tre non complanari. In tal modo si viene a stabilire una corrispondenza biunivoca tra i punti di uno spazio n-dimensionale e le ennuple ordinate di numeri reali. Se gli assi sono a due a due perpendicolari si ha un riferimento cartesiano ortogonale.
Sistema di riferimento polare
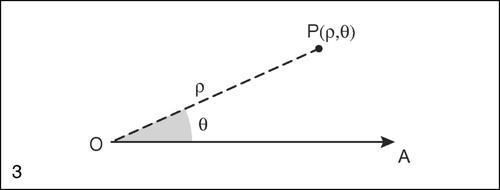
Oltre ai sistemi cartesiani esistono numerosi altri sistemi di riferimento, tra i quali il sistema di riferimento polare, che si ottiene fissando una semiretta OA (di origine O, detto polo), un’unità di misura sulla semiretta e un verso positivo di rotazione. In tal modo ogni punto del piano è in corrispondenza biunivoca, fatta eccezione per il punto O, con una coppia ordinata (ρ, θ) di numeri reali detti coordinate polari di P, con ρ ≥ 0, detto raggio vettore, che esprime la distanza di P dall’origine O, e θ ∈ (−π, π], detto argomento o anomalia, che misura l’angolo formato dalla semiretta fissa OA con il raggio vettore. Al polo O corrisponde ρ = 0 e θ indefinito.
Coordinate sferiche e cilindriche
L’estensione allo spazio tridimensionale del riferimento polare introdotto nel piano, può essere fatto con un sistema di → coordinate sferiche o con un sistema di → coordinate cilindriche.