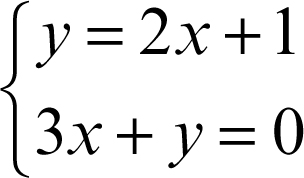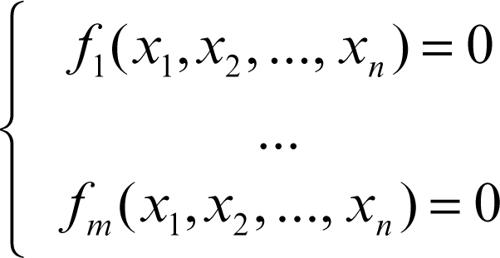sistema di equazioni

sistema di equazioni

sistema di equazioni insieme di equazioni delle quali si ricercano le soluzioni comuni. Un sistema si riconosce dal fatto che le equazioni sono presentate come una lista a cui è anteposta una parentesi graffa. Per esempio

è un sistema di due equazioni in due incognite. L’insieme di definizione di un sistema di equazioni è l’intersezione degli insiemi di definizione delle singole equazioni che lo compongono; risolvere un sistema di equazioni significa determinare le sue soluzioni, vale a dire determinare l’intersezione degli insiemi delle soluzioni delle singole equazioni che lo compongono.

Un sistema di equazioni che ammetta soluzioni è detto compatibile o risolubile, altrimenti esso è detto incompatibile o impossibile; un sistema di equazioni compatibile è detto determinato se ammette un numero finito di soluzioni, è detto invece indeterminato se ammette infinite soluzioni. Due sistemi di equazioni sono detti equivalenti se tutte le soluzioni dell’uno sono soluzioni dell’altro e viceversa. Due equazioni sono dette compatibili se è compatibile il sistema da esse determinato, in caso contrario esse sono dette incompatibili; sono infine dette indipendenti se il sistema da esse determinato non è equivalente a nessuna delle due equazioni date.

Un sistema di equazioni è in forma canonica se è della forma

dove x₁, …, x_n sono le incognite delle equazioni e dove ƒ₁, …, ƒ_m sono funzioni di x₁, …, x_n.

Nel caso particolare di un sistema di equazioni algebriche, in cui cioè le funzioni ƒ₁, …, ƒ_m sono funzioni che con opportune trasformazioni possono essere trasformate in polinomi, il grado del sistema è il prodotto dei gradi delle singole equazioni algebriche che lo compongono. L’insieme delle soluzioni di un sistema di equazioni algebriche, interpretato come insieme di punti in un opportuno spazio affine, costituisce, sotto opportune ipotesi, una → varietà algebrica. Nel caso di un sistema di due equazioni in due incognite a coefficienti complessi di grado rispettivamente m e n, le soluzioni del sistema sono mn, contate con la rispettiva molteplicità e contando anche eventuali soluzioni improprie (→ Bézout, teorema di): ciò equivale a dire che le due curve algebriche associate nel piano proiettivo alle due equazioni del sistema si intersecano esattamente in mn punti, contati con la rispettiva molteplicità.

Nel caso in cui le equazioni del sistema siano tutte lineari, vale a dire di grado 1, si ha un → sistema lineare, nel qual caso si dispone di una teoria completa per la sua risoluzione. Fatta eccezione per particolari sistemi di equazioni dotati di un numero elevato di simmetrie, nel caso generale di un sistema di equazioni non lineare la situazione è estremamente complessa e per la sua risoluzione si ricorre solitamente a → metodi numerici.