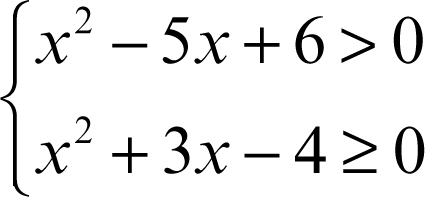sistema di disequazioni

sistema di disequazioni

sistema di disequazioni insieme di disequazioni delle quali si ricercano le soluzioni comuni. Le disequazioni che fanno parte di un sistema sono precedute da una parentesi graffa. L’insieme di definizione di un sistema di disequazioni è l’intersezione degli insiemi di definizione delle singole disequazioni che lo compongono. Risolvere un sistema di disequazioni significa determinare le sue soluzioni, vale a dire determinare l’intersezione degli insiemi delle soluzioni delle singole disequazioni che lo compongono. Un sistema di disequazioni che ammetta soluzioni è detto compatibile o risolubile, altrimenti esso è detto incompatibile o impossibile, e il suo insieme delle soluzioni è quindi vuoto. Due disequazioni sono dette compatibili se è compatibile il sistema da esse determinato, in caso contrario esse sono dette incompatibili.

Nel caso di un sistema di disequazioni in un’incognita è possibile rappresentare graficamente su una retta, dotata di un sistema di riferimento, l’insieme delle soluzioni di ciascuna disequazione; allora l’insieme delle soluzioni del sistema sarà l’unione degli intervalli reali ottenuti intersecando gli intervalli in cui le singole disequazioni sono verificate. L’insieme degli elementi estremali di tali intervalli coincide con l’insieme delle soluzioni delle equazioni associate alle singole disequazioni che compongono il sistema. Se le disuguaglianze che compaiono nel sistema sono tutte strette, allora tali elementi non appartengono all’insieme delle soluzioni del sistema e gli intervalli che compongono l’insieme delle soluzioni del sistema sono tutti aperti; in caso contrario compaiono in generale intervalli chiusi o chiusi solamente da un lato. Per esempio, nel sistema di disequazioni

la prima disequazione ha come insieme delle soluzioni l’unione delle due semirette aperte

mentre la seconda disequazione ha come insieme delle soluzioni l’unione delle due semirette con frontiera {x ∈ R : x ≤ −4 o x ≥ 1}. L’insieme delle soluzioni del sistema è allora

Nel caso di sistemi di disequazioni lineari in due incognite, l’insieme delle soluzioni (non vuoto) di ognuna delle disequazioni è rappresentato nel piano cartesiano da un semipiano; l’insieme delle soluzioni di un tale sistema è allora una regione convessa del piano avente come contorno una spezzata e, se la regione è finita, un poligono.