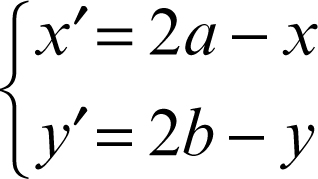simmetria centrale

Enciclopedia della Matematica (2013)

simmetria centrale


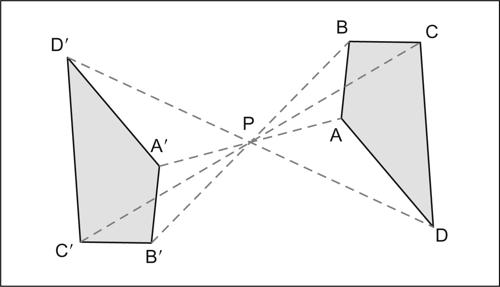
simmetria centrale in geometria, particolare trasformazione isometrica del piano o, più in generale, di uno spazio di dimensione qualunque, per cui, fissato un punto O detto centro di simmetria, a ogni punto P corrisponde il punto P′ tale che O risulti il punto medio del segmento PP′. È una trasformazione involutoria (coincide con la propria inversa e composta con sé stessa dà l’identità) e diretta (non modifica l’orientamento del piano). Nello spazio tridimensionale la simmetria centrale, a differenza di quanto accade nel piano, è una isometria invertente. Essendo una → isometria ne ha tutti gli invarianti: inoltre, ha come invariante le direzioni e l’unico suo punto fisso è il centro di simmetria mentre le rette passanti per tale centro sono tutte e sole le rette unite. La simmetria centrale si identifica nel piano con una rotazione attorno al centro di un angolo piatto e si ottiene anche come composizione di due simmetrie assiali con assi perpendicolari. Pertanto tutte le figure che presentano due simmetrie rispetto a due assi tra loro perpendicolari (come per esempio il rombo o il rettangolo) sono simmetriche centralmente. Non è però vero il viceversa: per esempio, un parallelogramma che non sia né rettangolo né rombo è simmetrico rispetto al punto di intersezione delle diagonali, ma non ha alcun asse di simmetria. La composizione di due simmetrie centrali, di rispettivi centri O e O′, è una traslazione di vettore

formula

Nel piano dotato di un riferimento cartesiano Oxy le equazioni di una simmetria centrale di centro C(a, b) sono:

formula
SIMMETRIA CENTRALE NEL PIANO

Vedi anche
figura simmètrica In geometria, si dice simmetrica (centralmente, assialmente o rispetto a un piano) una figura che corrisponde a sé stessa in una simmetria. Per es. il triangolo equilatero è una f.s. assialmente rispetto a tre assi, mentre il cerchio è una f.s. centralmente e rispetto ai suoi infiniti diametri. cubo Poliedro regolare che ha per facce sei quadrati uguali, da cui l’altro nome di esaedro regolare. Possiede un centro di simmetria (il punto in cui concorrono le 4 diagonali, tra di loro uguali), che è centro della sfera iscritta e di quella circoscritta al cubo stesso. Se l è la lunghezza comune degli ... poliedro Solido geometrico limitato da un numero finito di poligoni disposti in modo tale che ciascun lato sia comune a due e a due soli poligoni (come, per es., nel cubo, nelle piramidi, nei prismi): facce del p. sono i poligoni che lo limitano; spigoli, vertici del p. rispettivamente i lati e i vertici degli ... simmetria Distribuzione ordinata delle parti di un oggetto tale che si possa individuare un elemento geometrico (un punto, una linea, una superficie) rispetto al quale a ogni punto dell’oggetto posto da una parte di esso corrisponda, a uguale distanza, un punto dall’altra parte. Con significato più generico, disposizione ...
Tag
Vocabolario
simmetrìa
simmetria simmetrìa s. f. [dal gr. συμμετρία, comp. di σύν «con» e μέτρον «misura»]. – 1. Ordinata distribuzione delle parti di un oggetto (di un edificio, di una struttura, di un’opera d’arte, ecc.) tale che si possa individuare un elemento...
centrale
centrale agg. e s. f. [dal lat. centralis, der. di centrum «centro»; l’uso sostantivato si ha per ellissi di sede, officina e sim.]. – 1. agg. a. Del centro, che costituisce il centro: punto, parte, idea, problema centrale. b. In geografia,...