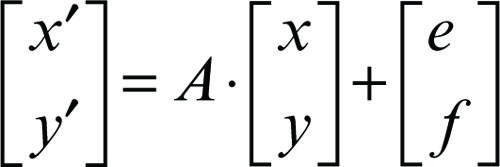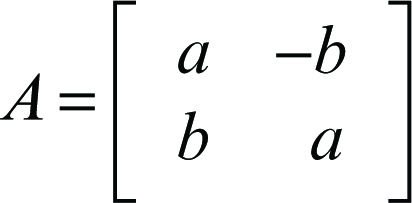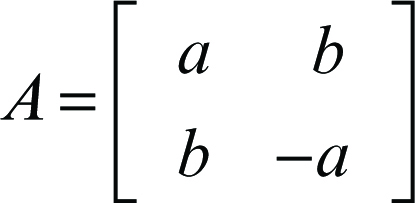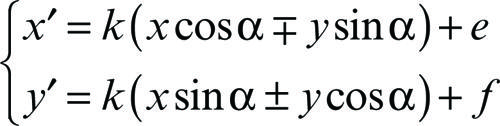similitudine
similitudine
similitudine termine che indica una relazione di → equivalenza, ma che assume diversi significati a seconda del contesto.
☐ Nel calcolo letterale, è la relazione che si stabilisce tra monomi che hanno identica parte letterale. Due monomi possono addizionarsi soltanto se sono monomi simili. La loro somma ha come coefficiente numerico la somma algebrica dei coefficienti dei monomi addendi e come parte letterale la loro comune parte letterale: così, per esempio, 2a2b3 + 7a2b3 = 9a2b3.
☐ In algebra lineare, è la relazione che si stabilisce tra matrici quadrate dello stesso ordine. Si dice che due matrici A e A′ sono simili quando esiste una matrice invertibile P tale che risulti A′ = P−1AP.
☐ In geometria, il termine indica sia una particolare trasformazione geometrica sia la relazione che si stabilisce tra le figure quando l’una risulti essere la corrispondente dell’altra in tale trasformazione. Come trasformazione in sé di uno spazio metrico o proiettivo, la similitudine è una → affinità che a due qualsiasi punti distinti A e B associa due punti A′ e B′ tali che il rapporto tra il segmento A′B′ e il segmento AB è una costante reale k ≠ 0, detta rapporto di similitudine. Se |k| = 1 si ha in particolare una → isometria (e si chiama congruenza la relativa relazione), se |k| > 1 si ha un ingrandimento, se |k| < 1 si ha una riduzione. Il prodotto di due similitudini, i cui rispettivi rapporti di similitudine sono k1 e k2, è una similitudine di rapporto k1 ⋅ k2. Le similitudini, rispetto alla composizione di trasformazioni, formano un gruppo, sottogruppo del gruppo delle affinità e contenente il gruppo delle isometrie.
Nel piano, una similitudine può essere ottenuta come prodotto di una → omotetia e una isometria e quindi i suoi invarianti caratteristici sono:
• le ampiezze degli angoli;
• i rapporti tra i segmenti.
Inoltre, una similitudine che non sia una → traslazione ha sempre un punto fisso, che corrisponde cioè a sé stesso, detto centro della similitudine. Si fa distinzione tra similitudini dirette, che mantengono l’orientamento del piano, e similitudini inverse o invertenti, che mutano tale orientamento. In ogni caso, due figure che si corrispondono in una similitudine sono dette figure simili. Tale relazione è una equivalenza e le figure tra loro simili sono caratterizzate dall’avere la stessa forma. Nel piano, sono tra loro simili tutti i cerchi, tutte le parabole e tutti i poligoni regolari con lo stesso numero di lati. Due poligoni sono simili quando hanno segmenti corrispondenti in proporzione e angoli di uguale ampiezza; se k è il rapporto di similitudine, il rapporto tra le loro aree è k 2. In particolare, per i triangoli esistono criteri che fissano alcune condizioni sufficienti per stabilire la loro similitudine (→ similitudine, criteri di (per i triangoli)).
Nel piano dotato di riferimento cartesiano Oxy le equazioni di una similitudine, in forma matriciale, sono
dove
se la similitudine è diretta (e infatti det(A) > 0, non essendo a e b entrambi nulli) oppure
se la similitudine è invertente (e det(A) < 0). In ogni caso
è il rapporto di similitudine.
Per sottolineare il fatto che la similitudine è il prodotto di una omotetia e una isometria le equazioni di una similitudine sono talvolta scritte nella forma equivalente
Le caratteristiche della similitudine si estendono allo spazio tridimensionale: una similitudine nello spazio è una affinità spaziale (cioè una omografia in cui il piano all’infinito è unito e, quindi, corrisponde a sé stesso), nella quale si mantiene il rapporto |k| tra segmenti corrispondenti. Si conservano quindi le ampiezze angolari, mentre i volumi tra solidi corrispondenti sono in rapporto k 3.