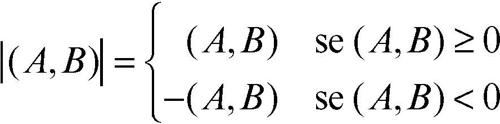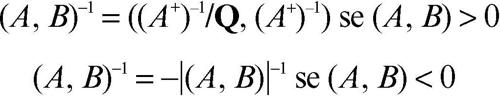Dedekind, sezione di

Dedekind, sezione di

Dedekind, sezione di o taglio di Dedekind, nozione introdotta da R. Dedekind alla fine del secolo xix nell’intento di precisare il concetto di ordinamento continuo e fornire una costruzione formale dell’insieme R dei numeri reali a partire dai numeri razionali. La sezione di Dedekind di un insieme X dotato di un ordinamento ≤ è una partizione di X in due sottoinsiemi A e B tale che: ∀a ∈ A, ∀b ∈ B, a ≤ b (e quindi, poiché si tratta di una partizione, vale a < b). Una tale sezione è indicata con il simbolo (A, B). Per esempio una sezione di Dedekind dell’insieme Q dei numeri razionali, dotato dell’ordinamento ordinario, è la coppia (A, B), dove A = {x ∈ Q: x 2 ≤ 2 oppure x ≤ 0}, B = {x ∈ Q: x 2 ≥ 2 e x ≥ 0}. Si consideri a tal fine l’insieme S delle sezioni di Dedekind di Q. Una sezione di Dedekind (A, B) di Q è detta di prima specie se A ammette massimo, è detta di seconda specie se B ammette minimo, presenta invece una lacuna se né A ammette massimo né B ammette minimo. Non può aversi il caso che A abbia massimo e B abbia minimo perché altrimenti Q sarebbe discreto. Un elemento separatore di una sezione (A, B) è un numero razionale x tale che, per ogni a appartenente ad A e per ogni b appartenente a B, risulta a ≤ x o x ≤ b: mentre ogni sezione di prima o seconda specie determina un elemento separatore (che coincide con il massimo di A o con il minimo di B), si ha una lacuna se la sezione è priva di elemento separatore. Si definisce quindi l’insieme R dei numeri reali come l’insieme ottenuto da S identificando tra di loro le sezioni di Dedekind che ammettono lo stesso elemento separatore. L’ordinamento totale ≤ definito in Q si estende in modo naturale all’insieme R così definito ponendo

La relazione così definita costituisce un ordinamento totale, rispetto al quale R è denso (→ densità), archimedeo (→ Archimede, assioma di) e completo, nel senso che è soddisfatto l’assioma di → Dedekind.

L’insieme R così definito contiene inoltre una copia di Q (a esso isomorfa come insieme ordinato) ottenuta associando a ogni numero razionale q la sezione di Dedekind (di prima o seconda specie) che ammette q come elemento separatore; l’insieme dei numeri irrazionali si identifica invece con l’insieme delle lacune.

All’insieme R dei numeri reali così definito possono infine essere estese le operazioni di addizione e moltiplicazione definite in Q. Se A e B sono due sottoinsiemi di Q, si definiscono a partire da essi i seguenti sottoinsiemi di Q: A + B = {a + b : a ∈ A, b ∈ B}; A · B = {a · b : a ∈ A, b ∈ B}; A/Q = Q − A; A+ = {a : a ∈ A, a > 0}; A−1 = {a−1 : a ∈ A}, dove nella definizione di A−1 si suppone che zero non appartenga ad A. Se (A, B) e (C, D) sono due sezioni di Dedekind, si definisce allora

tale operazione rende R un gruppo commutativo, con elemento neutro la sezione nulla 0 = (Q− ∪ {0}, Q+) (dove il primo termine della coppia è l’unione dell’insieme dei razionali negativi e dell’insieme costituito dal solo razionale 0, il secondo termine è l’insieme dei numeri razionali positivi) e dove l’opposto di una sezione (A, B) è la sezione

Una sezione di Dedekind (A, B) si dice positiva (rispettivamente non negativa) se 0 < (A, B) (rispettivamente se 0 ≤ (A, B)); si dice negativa (rispettivamente non positiva) se (A, B) < 0 (rispettivamente se (A, B) ≤ 0).

Si definisce dunque la moltiplicazione tra sezioni di Dedekind non negative come

se (A, B) ≥ 0, (C, D) ≥ 0.

Si indichi con sgn(A, B) il segno di una sezione di Dedekind, vale a dire

e con |(A, B)| il modulo di una sezione di Dedekind, vale a dire

in modo che il modulo di una sezione di Dedekind è una sezione di Dedekind non negativa.

Si definisce dunque la moltiplicazione tra sezioni di Dedekind arbitrarie come

dove la moltiplicazione tra segni segue le usuali regole formali + · + = − · − = + e + · − = − · + = −. Insieme alla già definita operazione di addizione, tale operazione rende R un campo, con elemento neutro moltiplicativo la sezione unità 1 = ({x ∈ Q, x < 1}, {x ∈ Q, x ≥ 1}) e dove l’inverso di una sezione non nulla è dato da:

Tale struttura di campo è inoltre compatibile con la struttura d’ordine già definita ed è compatibile con la struttura di campo già definita in Q: pertanto R assume la struttura di campo ordinato e Q si identifica con un suo sottocampo.

La costruzione di R a partire da Q, ottenuta da Dedekind attraverso le sezioni, risulta equivalente a quella effettuata mediante le successioni di Cauchy di numeri razionali (→ Cantor, definizione di numero reale di).