sezione aurea
sezione aurea
sezione aurea divisione di un segmento in due parti tali che la parte maggiore sia medio proporzionale fra l’intero segmento e la parte minore. In altri termini, dato un segmento AB, la sezione aurea è la sua parte AP che risulta medio proporzionale tra tutto AB e la sua parte rimanente: AB : AP = AP : PB. Si dice, seguendo Euclide nel xiii libro degli Elementi, che il segmento è suddiviso in «media ed estrema ragione», da cui il termine sezione che indica l’individuazione di un particolare punto e, per estensione, un segmento che ha questo punto per estremo. Risulta a sua volta che PB è la sezione aurea di AP. Ponendo uguale a 1 il segmento AB e indicando con x la sua sezione aurea, dalla proporzione 1 : x = x : (1 − x) si ricava come soluzione positiva
che esprime quindi la sezione aurea del segmento unitario. Il rapporto tra un segmento e la sua sezione aurea è il cosiddetto numero aureo
che è un numero irrazionale algebrico (→ numero algebrico) che risulta anche il limite a cui tende il rapporto tra due elementi consecutivi della successione di → Fibonacci. Si dice che due grandezze sono in proporzione aurea se hanno come rapporto Φ. In modo simile, ma non identico, si attribuisce il nome di angolo aureo all’angolo di circa 137,5° tale che l’angolo giro è in proporzione aurea con il suo esplementare (→ angoli associati (per ampiezza)).
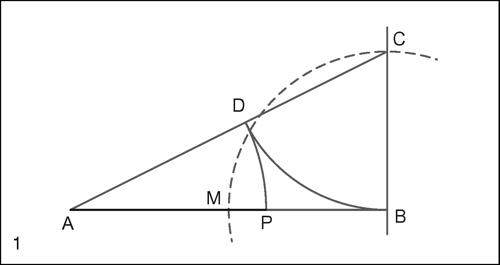
Costruzione della sezione aurea
La costruzione della sezione aurea di un segmento AB è un problema risolubile con riga e compasso. Costruito il punto M medio del segmento AB e tracciata la perpendicolare per B al segmento AB, con centro in B si traccia l’arco MC, essendo C un punto sulla perpendicolare per B, e si conduce il segmento AC; con centro in C si traccia quindi l’arco BD, essendo D un punto di AC. Infine, con centro in A si traccia l’arco DP, essendo P un punto di AB. Il segmento AP così ottenuto è la sezione aurea di AB. La sezione aurea è costruibile anche a partire dal pentagono regolare, dal momento che il rapporto tra la diagonale di un pentagono regolare e il suo lato è il rapporto aureo; anche i punti di intersezione delle diagonali del pentagono regolare dividono le diagonali stesse in due segmenti fra cui sussiste un rapporto aureo. Forse anche per questo il pentagramma o pentagono stellato (cioè il pentagono con la stella a cinque punte formata dalle sue diagonali) fu il simbolo della scuola pitagorica.
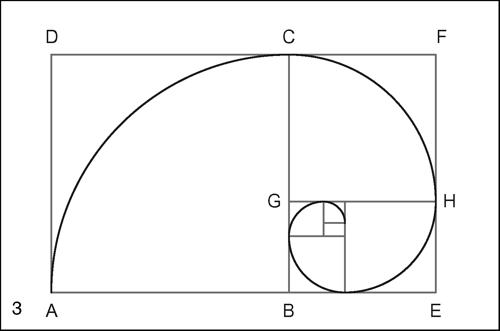
Costruzione del rettangolo aureo
Un rettangolo i cui lati sono in proporzione aurea è detto rettangolo aureo. A partire da un segmento AB, esso si costruisce in questo modo: si costruisce innanzitutto il quadrato ABCD, prolungando il lato AB, per esempio dalla parte di B; con centro in M, punto medio di AB, si traccia quindi un arco di raggio MC che interseca il prolungamento di AB in un punto E. Il rettangolo AEFD, di lati AE ed EF, è un rettangolo aureo. Risultano aurei anche il rettangolo BEFC e il rettangolo ottenuto togliendo dal rettangolo BEFC un quadrato di lato CF. Poiché ogni rettangolo ottenuto da un rettangolo aureo togliendo il quadrato costruito sul lato minore è ancora un rettangolo aureo, iterando il processo si ottiene una successione di punti posti su una curva detta spirale aurea, che è una particolare spirale logaritmica (→ spirale).
La sezione aurea in arte e in natura
La sezione aurea AP di un segmento AB genera una nuova sezione aurea: il segmento residuale PB è infatti a sua volta sezione aurea di AP. Analogamente, togliendo a un rettangolo aureo un quadrato, si ottiene un nuovo rettangolo aureo. Tali proprietà ricorsive sono alla base della presenza della sezione aurea in molti fenomeni naturali. In botanica, per esempio, quando si forma un nuovo singolo organo, quale una foglia, questo, per non essere oscurato, si dispone a una distanza angolare dal precedente costante e pari a circa un angolo aureo. La sezione aurea, che Luca Pacioli denominò divina proporzione e di cui illustrò le caratteristiche in un testo del 1509 (De divina proportione), ha attratto, a partire del rinascimento, l’attenzione non soltanto dei matematici, ma anche di pittori, scultori e architetti come canone di armonia e bellezza (→ architettura e matematica; → arte e matematica). Un tipico esempio è la riproposizione leonardesca del canone di rappresentazione della figura umana di Vitruvio, che colloca l’ombelico in una posizione tale da determinare la sezione aurea dell’intera figura. Molte attribuzioni di proporzioni auree a capolavori dell’arte o dell’architettura (per esempio a parti del viso della Gioconda di Leonardo da Vinci) appaiono forzate e non documentate. Nel xx secolo, tuttavia, l’architetto svizzero Le Corbusier (1887-1965) propose uno schema costruttivo per le abitazioni in armonia con le proporzioni del corpo umano denominato Modulor e basato su rapporti aurei.