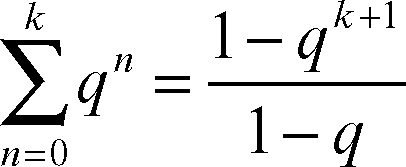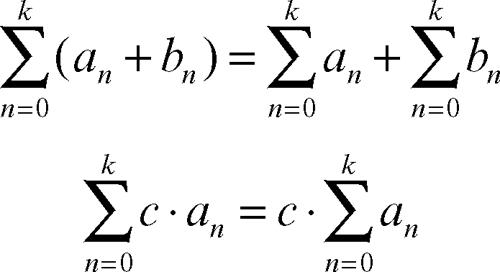serie numerica

serie numerica

serie numerica in analisi, scrittura formale che esprime l’addizione di infiniti addendi numerici (→ serie).

Più formalmente, data una successione di numeri a_n, con n ∈ N, detti termini della serie, si costruisce la successione delle ridotte, o somme parziali,

Si considera quindi il limite

Se tale limite esiste finito e vale S, si dice che la serie

converge e ha per somma S; si scrive allora:

Se il limite è infinito, si dice che la serie diverge, eventualmente specificando se diverge a +∞, a −∞ o a ∞ senza segno. Infine, se il limite non esiste si dice che la serie oscilla o che è indeterminata.

Si chiama resto k-esimo della serie la serie

ottenuta considerando solo i termini di indice n > k. Il carattere della serie (cioè il fatto che sia convergente, divergente o indeterminata) coincide con quello delle serie resto. Se esse convergono, si ha S = s_k + R_k e quindi il resto misura l’errore che si commette se si esegue la valutazione numerica di S arrestandosi alla somma s_k. Soltanto in pochi casi è possibile stabilire il carattere della serie mediante l’espressione analitica delle ridotte s_n; tra questi si segnalano i seguenti:

• serie geometrica: a_n = qⁿ, dove q è la ragione della progressione geometrica, di primo termine 1, corrispondente alla serie (→ serie geometrica). Si ha infatti, per q ≠ 1:

se invece q = 1

da cui si deduce che la serie geometrica è convergente a

mentre diverge a +∞ se q ≥ 1, a ∞ se q < −1, e infine oscilla se q = −1;

• serie di → Mengoli e sue generalizzazioni, così come tutte le serie telescopiche.

In generale, per riconoscere il carattere di una serie si deve tuttavia fare ricorso a dei criteri, cioè a delle condizioni (necessarie e/o sufficienti) per la convergenza, che comportano solo la conoscenza dei termini della serie (→ serie numerica, criteri di convergenza). È spesso utile distinguere le serie numeriche in base ad alcune caratteristiche algebriche dei termini che le compongono. Si parla di serie a termini positivi se tutti i termini della serie hanno segno positivo (o, se alcuni termini possono essere nulli, di serie a termini non negativi), di serie a termini di segno alterno, se si alternano appunto termini positivi e termini negativi, oppure, nel caso più generale, di serie a termini di segno qualunque. Quanto alla convergenza valgono per le serie numeriche le stesse distinzioni tra convergenza semplice e convergenza assoluta, introdotte per le serie in generale. La definizione “classica” di convergenza non è l’unica possibile, anche se è la più naturale; per diversi scopi nel xix secolo sono stati introdotti diversi metodi di → sommazione che generalizzano tale definizione.

Poiché valgono la proprietà commutativa dell’addizione e la proprietà distributiva della moltiplicazione rispetto all’addizione, il simbolo di sommatoria finita gode di proprietà di linearità:

Tali proprietà si estendono alle serie numeriche convergenti: se due serie sono convergenti e hanno come rispettive somme S₁ e S₂, la serie somma, ottenuta sommando le serie date, termine a termine, converge e ha somma S₁ + S₂; analogamente per la differenza (proprietà di additività delle serie numeriche). Se una delle due serie non converge, allora anche la serie somma non converge. Se la serie numerica

converge e ha somma S, allora la serie

converge e ha somma cS (proprietà di linearità delle serie numeriche).