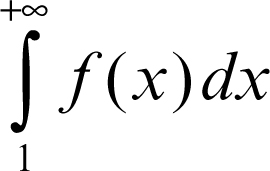serie numerica, criteri di convergenza per una

serie numerica, criteri di convergenza per una

serie numerica, criteri di convergenza per una condizioni necessarie e/o sufficienti per stabilire se una serie numerica converge (diverge o è indeterminata). Il criterio di → Cauchy dà una condizione necessaria e sufficiente per la convergenza della serie

e basta per esempio per garantire che la serie armonica

diverge. Una condizione necessaria per la convergenza è data dalla condizione

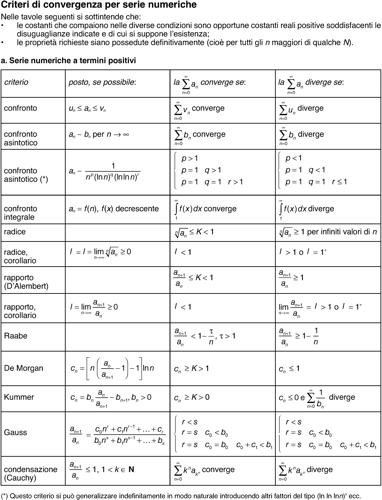
Le condizioni sufficienti (cui usualmente ci si riferisce con il termine criteri) per le serie numeriche si suddividono in:

• criteri per serie a termini positivi (o non negativi);

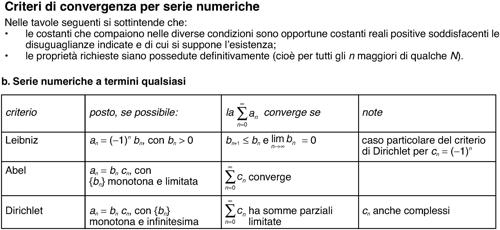
• criteri per serie con termini di segno alterno;

• criteri per serie con termini di segno qualsiasi (o nel campo complesso, per esempio il criterio di → Abel).

Per le serie a termini di segno alterno il criterio principe (e sostanzialmente unico) è il criterio di → Leibniz. Per serie generiche, l’unica possibilità generale è quella di verificare la assoluta convergenza, e quindi di ricondursi a serie a termini positivi. Moltissimi sono invece i criteri che sono stati introdotti, soprattutto nel xix secolo, per studiare casi sempre più complicati di serie a termini positivi. Dopo aver notato che una serie a termini non negativi può solo convergere o divergere a +∞, si stabilisce il criterio del confronto. Va premesso che la serie

si dice maggiorata dalla serie

se, per ogni n ∈ N, risulta a_n ≤ v_n, e minorata dalla serie

se, per ogni n ∈ N, si ha u_n ≤ a_n (rispettivamente le altre due serie sono dette maggiorante e minorante). Il criterio del confronto stabilisce allora che la serie

converge se una sua serie maggiorante

converge, e diverge se diverge una sua serie minorante

Usualmente la scelta degli u_n o dei ν_n si esegue in modo da semplificare l’espressione dei termini e ricondursi a una serie nota, per esempio la serie geometrica o una serie armonica generalizzata. Al criterio del confronto si riconducono i classici criteri: il criterio del rapporto, o criterio di d’→ Alembert, e quello della radice che stabilisce che la serie a termini non negativi

converge se, posto se possibile

si ha l < 1, mentre diverge se l > 1 o l = 1⁺. Al criterio del confronto si riconducono anche i criteri più articolati di → Raabe, → De Morgan e → Kummer.

Il criterio del confronto si estende considerando il rapporto tra due serie con il cosiddetto criterio del confronto asintotico che stabilisce che se a_n ∼ b_n per n → ∞, allora

converge (diverge) se

converge (diverge). Un analogo criterio di confronto si può stabilire confrontando la serie con un → integrale improprio ed è detto criterio integrale di convergenza: date una serie

a termini positivi e non crescenti e una funzione ƒ(x) definita per ogni x ≥ 1, tale che ƒ(n) = a_n per ogni n, allora se l’integrale improprio

è convergente, converge anche la serie data; se è divergente, diverge anche la serie data.

Altri criteri di convergenza sono quello di condensazione, dovuto a Cauchy, e il criterio di → Gauss, che si applica ogniqualvolta il rapporto a_n+1/a_n tra due termini successivi si esprime come una funzione razionale di n. Questi criteri sono riportati nelle tavole dei criteri di convergenza per una serie numerica.