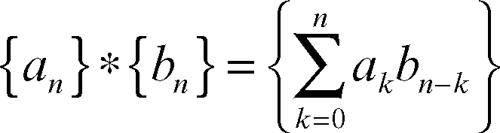serie formali, anello delle

serie formali, anello delle

serie formali, anello delle dato un anello A commutativo con unità e considerato l’insieme di tutte le successioni infinite di elementi di A, indicato con A^N, si definiscono tra due suoi elementi (cioè due successioni di elementi di A) l’addizione

e la moltiplicazione di → convoluzione (però discreta)

L’insieme A^N, con tali due operazioni, ha la struttura di anello commutativo con unità ed è detto anello delle serie formali. Elemento neutro per l’addizione è la successione {0} formata da tutti zeri, mentre elemento neutro per la moltiplicazione è la successione 1, 0, 0, …

Un qualsiasi elemento a ∈ A può essere identificato con la successione che ha come primo termine a e tutti gli altri termini uguali a 0. Se si indica con x la successione {x} = 0, 1, 0, 0, … si osserva che x ∗ x = x ² = x. Allora una qualsiasi successione {s}, qui di seguito indicata semplicemente con s, che sia quasi ovunque nulla (cioè presenti un numero finito r di termini non nulli) può essere scritta in modo del tutto formale come somma finita nel seguente modo:

Questa scrittura comporta la possibilità di indicare s come particolare somma:

Si giustifica così per essa il nome di polinomio formale con coefficienti nell’anello A e si giustifica altresì il fatto che alla sua estensione infinita si dia il nome di serie formale di potenze.