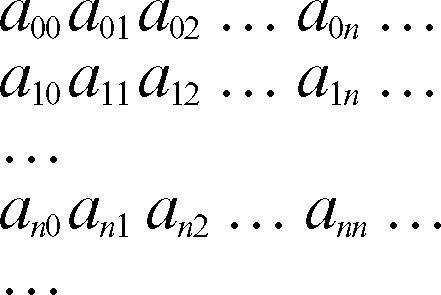serie doppia
serie doppia
serie doppia serie multipla i cui termini dipendono da due indici. Se si considera una successione i cui elementi sono a loro volta successioni, del tipo
si possono considerare vari tipi di somme parziali dei termini; per esempio, la somma eseguita per diagonali o quella eseguita per quadrati a partire da a00 (la cui scrittura estesa è: a00 + (a01 + a11 + a10) + (a02 + a12 + a22 + a21 + a20) +…). Ciascuna di queste costituisce una successione a doppio indice del tipo
che è una serie doppia, poiché indicata da due indici. Si possono considerare somme parziali a due indici
e se tali somme, dette ridotte di indici p e q della serie doppia, tendono a un valore finito al tendere all’infinito degli indici, la serie è convergente; se tendono all’infinito la serie è divergente; è invece indeterminata negli altri casi. Se il limite è calcolato facendo tendere all’infinito prima un indice poi l’altro la serie si dice iterata.
Il carattere della serie doppia può variare a seconda del tipo di somme parziali scelto; se però la serie è assolutamente convergente secondo un tipo di sommazione, lo è anche secondo gli altri, e converge sempre alla stessa somma, alla quale convergono anche le due serie iterate. Vale un criterio generale di convergenza: affinché una serie doppia sia convergente è necessario, ma non sufficiente, che sia
Alcuni criteri di convergenza per le serie (semplici) si estendono anche alle serie doppie.