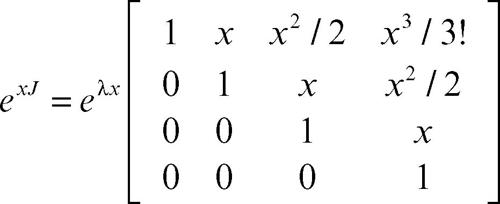matrici, serie di

Enciclopedia della Matematica (2013)

matrici, serie di

matrici, serie di estensione delle serie di → Maclaurin (e di → Taylor) da variabili complesse a matrici. Si consideri per esempio la serie esponenziale

e al posto della variabile z si sostituisca una matrice quadrata A; si ottiene la serie di matrici

Poiché il raggio di convergenza della serie è +∞, questa serie di matrici converge per ogni A, e la sua somma si può coerentemente denotare con la matrice esponenziale e^A. Si noti però che se le due matrici A e B non commutano, risulta in genere e^A+B ≠ e^Ae^B. Vale invece, per ogni coppia di reali x e t, l’uguaglianza e^xAe^tA = e^tAe^xA = e^(x+t)A. Questa proprietà è importante perché consente alla matrice e^xA di ammettere come derivata rispetto a x la matrice Ae^xA, e pertanto di esprimere l’integrale generale del sistema di equazioni differenziali a coefficienti costanti y′= Ay nella forma y(x) = e^xAc, con c vettore costante arbitrario, il cui significato si ottiene ponendo x = 0: si ha dunque c = y(0), sicché l’espressione y(x) = e^xAy(0) rappresenta la soluzione del problema di → Cauchy. Siccome è poi

la matrice e^tA viene detta matrice di trasferimento, perché “trasferisce” la condizione iniziale da un punto x a un punto x + t.

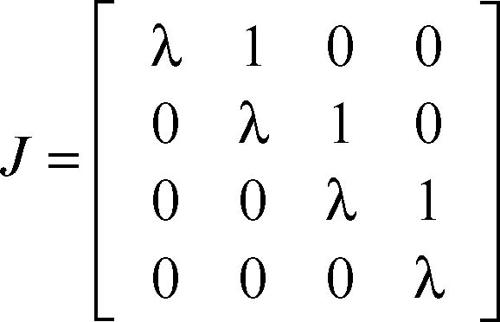
La formula è resa utilizzabile nella pratica dal fatto che il calcolo dell’esponenziale può essere eseguito senza far uso della serie. Infatti se la matrice A è diagonalizzabile (→ diagonalizzazione), si ha A = PDP⁻¹, e quindi Aⁿ{{{1}}}PDⁿP⁻¹, da cui e^A = Pe^DP⁻¹. Ma la matrice e^D ha forma diagonale, con exp(λ_k) sulla diagonale, dove λ_k sono gli autovalori di A, e quindi è facilmente calcolabile. Un procedimento analogo si può utilizzare nel caso in cui A non sia diagonalizzabile, mediante la forma canonica di Jordan (teorema di → Jordan per le matrici). Infatti dato il blocco

risulta

e quindi anche nel caso generale si può evitare l’uso della serie esponenziale. In modo analogo si possono definire, a partire da trascendenti intere ƒ(z), le matrici ƒ(A); in particolare, le matrici sinA, cosA, che si utilizzano nell’espressione simbolica della soluzione del sistema di equazioni del secondo ordine y″ + A²y = 0. Si possono anche definire serie di matrici a partire da serie di potenze con raggio di convergenza R < +∞; in tal caso però la convergenza della serie di matrici è subordinata alla condizione che una norma della matrice sia minore di R.