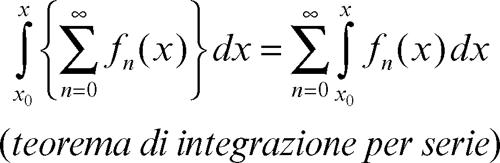serie di funzioni

Enciclopedia della Matematica (2013)

serie di funzioni


serie di funzioni serie i cui termini sono funzioni reali o complesse tutte definite in uno stesso insieme di un conveniente spazio complesso o reale. Limitandosi al caso di funzioni di una variabile reale, è una serie del tipo

formula

dove le funzioni ƒn(x) sono definite in uno stesso insieme D ⊆ R. Fissato x, si ha una serie numerica; i valori di x per cui tale serie converge formano l’insieme di convergenza puntuale E0 ⊆ D della serie di funzioni. È possibile anche considerare l’insieme E ⊆ E0 di convergenza uniforme (→ convergenza). Sotto opportune ipotesi è possibile estendere alle serie di funzioni le usuali proprietà analitiche delle somme; in particolare si hanno teoremi di passaggio al limite, di derivazione e di integrazione per serie.

Precisamente, detta ƒ(x) la somma della serie (uniformemente convergente), se x0 (che può anche essere ∞) è un punto di accumulazione di E ed esistono finiti i limiti

formula

e se la serie numerica

formula

converge, detta 1 la sua somma, risulta

formula

Senza la uniforme convergenza la tesi può non sussistere, per esempio:

formula

Se le funzioni ƒn(x) sono derivabili e se anche la serie delle derivate converge uniformemente in E, la somma ƒ(x) è derivabile e risulta

formula

Infine, se [x0, x] ⊆ E, si ha:

formula

Va osservato peraltro che per l’integrazione l’ipotesi di uniforme convergenza è eccessiva (si veda il concetto di convergenza dominata di Lebesgue in → Lebesgue, integrale di).

Vedi anche
serie Successione ordinata e continua di elementi, concreti e astratti, dello stesso genere. Ecologia Successione delle comunità che si sostituiscono l’una all’altra in una regione. Le comunità di transizione sono dette stadi seriali, quella terminale stabile è chiamata climax (➔). Poiché il climax varia ... integrale In matematica, operazione eseguita su una funzione di variabile reale o complessa per determinare l’area delimitata dalla funzione stessa e dall’intervallo su cui è definita. Il termine s’incontra per la prima volta in uno scritto di G. Bernoulli (1690); le denominazioni di i. definito e i. indefinito ... funzione Biologia L’attività propria di una cellula, o di una sua parte, o di un organo, o di un sistema organico. Oggetto di studio della fisiologia, è intimamente legata alla forma o struttura, oggetto di studio della morfologia. Forma e f. sono due aspetti sotto cui ci si presenta il fenomeno della vita. Non ... limite Livello massimo, al di sopra o al di sotto del quale si verifica un fenomeno. Fisica Angolo limite In ottica, nel passaggio di un raggio da un mezzo a un altro con indice di rifrazione assoluto inferiore (per es., per la luce visibile, dall’acqua all’aria) l’angolo di incidenza sulla superficie di separazione, ...
Tag
Vocabolario
ordine
ordine órdine s. m. [lat. ōrdo ōrdĭnis]. – 1. a. Disposizione regolare di più cose collocate, le une rispetto alle altre, secondo un criterio organico e ragionato, rispondente a fini di praticità, di opportunità, di armonia, e sim.: mettere,...
parte
parte s. f. [lat. pars partis]. – 1. a. Ciascuno degli elementi in cui un intero è diviso o può essere diviso, sia che essi siano materialmente staccati l’uno dall’altro, sia che possano essere soltanto considerati separatamente, per caratteristiche,...