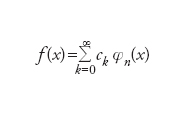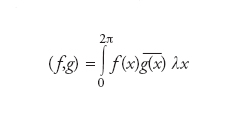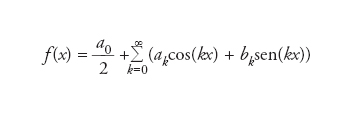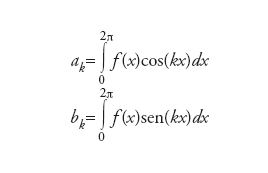serie di Fourier

serie di Fourier

L’espressione di una funzione f di una o più variabili reali per mezzo di un sistema di funzioni ortonormali. Più precisamente, sia F uno spazio vettoriale (completo) di funzioni di una variabile reale dotato di un prodotto scalare (∙,∙) (ovvero uno spazio di Hilbert) e una famiglia {φ_n, n=0,1,...} di suoi elementi (ovvero funzioni) tali che (φ_i,φ_j)=0 se i≠j e (φ_n,φ_n)=1 per ogni n. La famiglia {φ_n, n=0,1,...} è detta sistema ortonormale e se in aggiunta (f,φ_n)=0 per ogni n e f∈F implica f=0 essa è detta completa. Si dirà allora serie di Fourier di una funzione f l’espansione

dove i coefficienti c_k sono detti coefficienti di Fourier di F e sono espressi dalla formula c_k=(φ_k,f) e la serie si intende convergere nella norma indotta dal prodotto scalare. In altri termini, la serie di Fourier di una funzione f in uno spazio F è definita come lo sviluppo di f in termini di una base ortonormale fissata. In molte applicazioni matematiche e fisiche giocano un ruolo preminente funzioni di una variabile reale con periodo 2π, ovvero tali che f(0)=f(2π). Lo spazio F è allora lo spazio di Hilbert L²([0,2π]) delle funzioni a quadrato sommabile sull’intervallo chiuso [0,2π] dotato del prodotto scalare

e la base ortonormale {φ_n, n=0,1,...} scelta è costituita dalle funzioni trigonometriche (1/√2π)sen(nx), (1/√2π)cos(nx), n=0,1,...}. La serie di Fourier si scrive allora

con coefficienti

ovvero nella forma in cui apparve per la prima volta nel 1807 in un articolo di Fourier. Per questa ragione spesso con il termine serie di Fourier di una funzione f si intende proprio la sua serie di Fourier trigonometrica. Il problema della convergenza della serie di Fourier in senso più forte che nella norma dello spazio L²([0,2π]) (per esempio della convergenza uniforme) qualora la funzione f possieda proprietà di regolarità (per esempio sia continua o derivabile) ha una risposta nel teorema di Dirichlet.

→ Fisica matematica