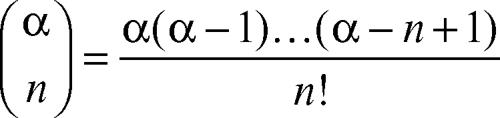serie binomiale

serie binomiale

serie binomiale sviluppo in serie di → Maclaurin della funzione

formula

dove

è il → coefficiente binomiale generalizzato ad α reale qualsiasi. La serie si riduce a un polinomio nel caso α ∈ N, in quanto tutti i coefficienti con n > α si annullano. Ha raggio di convergenza R = 1; sulla circonferenza di convergenza la serie converge assolutamente per α ≥ 0, semplicemente per −1 < α < 0, tranne che per z = −1 dove diverge, mentre diverge sempre per α ≤ −1.