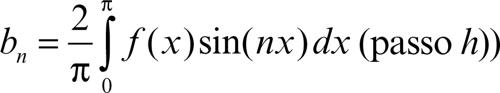separazione delle variabili, metodo di
separazione delle variabili, metodo di
separazione delle variabili, metodo di metodo per la risoluzione di equazioni differenziali alle derivate parziali lineari che consiste nei seguenti passi:
a) esprimere una soluzione come prodotto di funzioni, ognuna delle quali dipenda soltanto da una variabile;
b) riscrivere l’equazione come somma di addendi, ognuno dei quali dipenda soltanto da una variabile (in genere, si divide per la soluzione, supponendo che sia diversa da 0; questa condizione, anche se non verificata ovunque, non crea di solito problemi);
c) osservare che, affinché sia soddisfatta l’identità, ognuno di questi addendi deve essere costante;
d) “spezzare” quindi l’equazione differenziale alle derivate parziali in un sistema di equazioni differenziali ordinarie, ciascuna in una differente variabile, collegate tra loro dalle sole costanti introdotte (costanti di separazione);
e) risolvere tali equazioni;
f) imporre alle soluzioni ottenute di soddisfare opportune condizioni ai limiti, ereditate dall’equazione di partenza: si ottiene in tal modo un problema di → Sturm-Liouville, che fornisce, nei casi più comuni, una infinità numerabile di autovalori (cioè uno spettro discreto) e le corrispondenti autofunzioni;
g) ricostruire, mediante tali soluzioni, una infinità di soluzioni dell’equazione originaria e combinarle in una serie a coefficienti indeterminati;
h) utilizzare le condizioni rimaste (→ Cauchy, problema di, o altre) per determinare tali coefficienti, ottenendo così una possibile soluzione del problema proposto;
i) verificare a posteriori che siano soddisfatte (in qualche spazio funzionale) le ipotesi che permettono di eseguire i passaggi svolti in precedenza.
Per esempio, si consideri l’equazione del calore monodimensionale ut = σuxx in una sbarra di lunghezza π, con le condizioni u(0, t) = u(π, t) = 0, u(x, 0) = ƒ(x). Scritta la soluzione u(x, t) come prodotto X(x)T(t) di funzioni della sola x e della sola t (passo a)), si sostituisce tale espressione nell’equazione ottenendo X(x)T ′ (t)= σX ″(x)T(t), e quindi, dividendo per u: T ′(t)/T(t) = σX ″ (x)/X(x) (passo b)). A questo punto, il primo membro dipende solo da t, il secondo solo da x: perché possano essere identicamente uguali, è necessario che siano entrambi uguali a una costante, che per comodità si indichi con λσ (passo c)). Si ottengono così le equazioni T ′(t) − λσT(t) = 0 e X ″(x) − λX(x) = 0 (passo d)). La prima di esse ha integrale generale T(t) = Ceλσt, essendo C una costante arbitraria, e la seconda ha soluzioni dipendenti dal segno di λ (passo e)). Le condizioni al contorno u(0, t) = u(π, t) = 0 si traducono però nel problema ai limiti X(0) = X(π) = 0, che solo per λ = −n2 (autovalori) ammette le soluzioni non nulle X(x) = c sin(nx) (autosoluzioni) (passo ƒ)). Si moltiplicano tra loro le soluzioni X(x) e T(t) corrispondenti allo stesso valore di λ, e si sommano ottenendo la serie
a coefficienti indeterminati (passo g)). Questa è una serie di → Fourier di soli seni. Si impone ora che sia soddisfatta la condizione iniziale u(x, 0) = ƒ(x). Per t = 0 si ha:
condizione che resta soddisfatta scegliendo come coefficienti bn i coefficienti di Fourier dell’estensione dispari su [−π, 0] della funzione ƒ, cioè
Se il prolungamento dispari di periodo 2π di ƒ(x) risulta abbastanza regolare, di modo che i coefficienti bn siano O(1/n3+α), con α > 0 (si veda → O grande) è possibile derivare per serie due volte rispetto a x e una rispetto a t; la serie così ottenuta è una soluzione classica dell’equazione differenziale. Se tale prolungamento è meno regolare, la soluzione può essere ancora accettata in senso debole, in un opportuno spazio di → Sobolev, e comunque nel senso delle distribuzioni (passo i)).