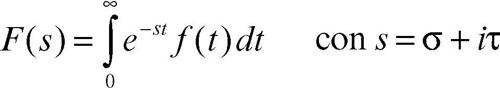convergenza, semipiano di
convergenza, semipiano di
convergenza, semipiano di semipiano del piano complesso Re(z) > α, in cui la trasformata (o la serie) converge; la nozione trova impiego soprattutto nelle trasformate di Laplace (→ Laplace, trasformazione di) e nelle serie di → Dirichlet. Nel caso della trasformata di Laplace si ha un integrale del tipo
il quale converge per valori di σ non inferiori a un numero α, detto ascissa di convergenza; sulla retta di convergenza σ = α l’integrale può convergere in alcuni punti e non convergere in altri. Per esempio, la trasformata di ƒ(t) = ekt è
convergente per Re{{{1}}} σ > k. A differenza del caso delle serie di potenze, è possibile che la convergenza assoluta dell’integrale sia garantita solo per valori σ > β, con β > α: si ha allora un semipiano di assoluta convergenza, e una striscia in cui la convergenza è semplice ma non assoluta. Un comportamento analogo presentano le serie di Dirichlet
