segnali cerebrali, analisi dei

segnali cerebrali, analisi dei

Una parte importante della conoscenza sulle funzioni cerebrali si basa sulla registrazione dei segnali elettrici neurali. Il segnale così ottenuto è però ambiguo da interpretare perché rappresenta il contributo di diversi eventi indipendenti. Per interpretare il segnale neurale è dunque necessario analizzarlo con tecniche matematiche volte sia a separare il contributo dei diversi fenomeni neurali sia a interpretarne la funzione nella dinamica cerebrale. Le tecniche più importanti per la separazione dei contributi neurali sono quelle di identificazione dei potenziali d’azione (impulsi) emessi da neuroni in vicinanza dell’elettrodo, e della classificazione degli impulsi emessi da ogni neurone. Le tecniche più rilevanti per l’interpretazione della funzione di un segnale cerebrale sono quelle di decodifica del segnale, che hanno il fine di ricostruire la causa che porta all’emissione del segnale considerato, e quelle derivate dalla teoria dell’informazione, che hanno il fine di caratterizzare la quantità di informazione fornita da ogni processo neurale. [➔ cervello, modelli per l’attività su larga scala del; codice di comunicazione neuronale; elettrofisiologia del sistema nervoso; informazione neurale; potenziale d’azione] L’analisi dei segnali cerebrali ottenuta tramite la registrazione dell’attività elettrica neurale fornisce informazioni rilevanti per la conoscenza della funzione cerebrale. Registrazioni extracellulari del segnale neurale sono di solito eseguite inserendo microelettrodi nel cervello e misurando il potenziale di campo elettrico generato dal flusso di correnti nello spazio extracellulare in seguito a vari tipi di eventi di attivazione neurale. Il segnale così ottenuto (segnale extracellulare) è però ambiguo da interpretare perché rappresenta il contributo di molti fattori potenzialmente diversi o indipendenti, come i potenziali d’azione emessi da diversi neuroni, l’attività sinaptica e numerosi altri fattori. Il primo passo per poter interpretare il segnale neurale è dunque quello di analizzarlo con tecniche matematiche volte a separare il contributo dei diversi fenomeni neurali che lo hanno generato. Siccome l’output dell’elaborazione elementare effettuata da ogni singolo neurone consiste in una sequenza temporale di potenziali d’azione (che qui chiameremo impulsi), un tipo molto importante di analisi del segnale neurale consiste nell’identificazione degli impulsi emessi da diversi neuroni nella vicinanza dell’elettrodo. Il secondo passo è quello di capire il significato del messaggio che la sequenza di impulsi emessa da ogni singolo neurone comunica al resto del sistema nervoso.

Separazione dei segnali neurali in potenziali d’azione e potenziali locali di campo

Il segnale extracellulare ottenuto dai microelettrodi è innanzitutto amplificato e poi filtrato con filtri passabanda per ottenere due diverse componenti del segnale neurale: la componente ad alta frequenza e quella a bassa frequenza. La separazione del segnale in bande di alta e bassa frequenza viene eseguita per separare i potenziali d’azione (eventi ad alta frequenza che durano ca. 1 ms) dai contributi portati da altri tipi di eventi neurali più lenti, come l’attività sinaptica. La componente ad alta frequenza (ottenuta filtrando il segnale extracellulare in una banda di frequenza tipicamente delimitata tra i 300 e i 3.000 Hz) è quella più analizzata in quanto contiene gli impulsi neurali. La componente a bassa frequenza (ottenuta filtrando il segnale nella banda di frequenza 1÷200 Hz) è detta potenziale locale di campo (PLC) e viene usata per ottenere un’indicazione dell’attività sinaptica totale nella vicinanza dell’elettrodo. Il PLC può essere utile per valutare la presenza di effetti che, anche se importanti, non raggiungono la soglia necessaria per l’emissione di impulsi.

Individuazione degli impulsi neurali

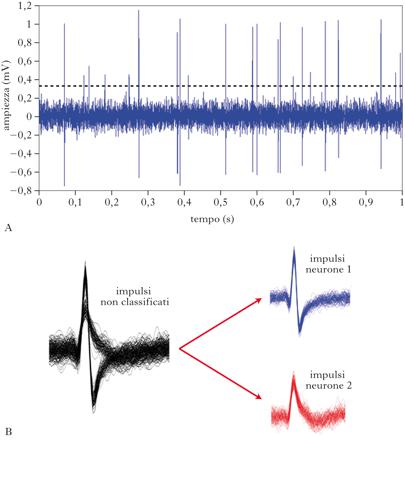
Il primo passo nell’analisi di segnali consiste nell’individuare la presenza di impulsi neurali nella serie temporale del segnale extracellulare. Per effettuare l’individuazione degli impulsi il segnale registrato dall’elettrodo extracellulare viene prima filtrato con filtri passabanda. Le frequenze sotto i 300 Hz sono tagliate per eliminare le fluttuazioni lente non collegate a emissioni di impulsi. Le frequenze sopra i 3.000 Hz sono tagliate per meglio visualizzare gli impulsi e ridurne il rumore.

Ampiezza degli impulsi nel segnale extracellulare

Il segnale extracellulare filtrato nella banda di alta frequenza presenta impulsi di altezza variabile. Le altezze rilevabili degli impulsi dipendono dalla distanza tra i neuroni che li hanno emessi e l’elettrodo. Neuroni abbastanza vicini alla punta dell’elettrodo (a una distanza di non più di 50÷100 mm) sono in grado di generare impulsi che vengono captati dall’elettrodo con un’ampiezza sufficiente da garantire un buon rapporto segnale-rumore per potere essere poi classificati e distinti in attività di neuroni singoli. Neuroni più distanti dalla punta dell’elettrodo (a distanze di circa 150 mm) emettono impulsi che possono essere identificati, ma che non possono essere più classificati come appartenenti a neuroni diversi a causa del loro meno elevato rapporto tra segnale e rumore. Impulsi emessi da neuroni ancora più distanti (alcune centinaia di micron o più) non possono nemmeno essere identificati. Soglia di identificazione Dopo il filtraggio, l’individuazione viene effettuata facendo uso di una soglia. Quando l’ampiezza del segnale neurale oltrepassa una certa soglia (positiva o negativa), si registra la presenza di un impulso. La scelta del valore di soglia è un compromesso tra diverse esigenze: se la soglia è troppo alta, l’algoritmo può non riuscire a rilevare impulsi invece presenti; se la soglia è troppo bassa, si ha il problema opposto, cioè l’erronea individuazione come impulsi di eventi che invece riflettono una fluttuazione casuale del segnale extracellulare attribuibile a rumore. La soglia può essere scelta manualmente dall’utente dopo aver ispezionato visivamente i dati, oppure essere determinata da un algoritmo automatico che calcola l’ampiezza del rumore, la compara con quella degli impulsi più alti e sceglie il valore di soglia corrispondente al compromesso migliore tra le esigenze sopraelencate. La scelta automatica è preferibile specialmente durante l’analisi di grandi quantità di dati, per es. quelle registrate simultaneamente da un gran numero di diversi elettrodi.

Classificazione degli impulsi neurali

Il secondo passo nell’analisi di segnali consiste nel determinare da quanti neuroni diversi sono stati emessi gli impulsi e nell’assegnare ogni impulso al neurone che lo ha emesso. In linea di principio, il modo più semplice di separare gli impulsi emessi da neuroni diversi è di usare un discriminatore basato sulla ampiezza degli impulsi. Il problema di questa semplice tecnica è però che gli impulsi di diversi neuroni possono spesso avere ampiezza simile, ma forme molto diverse. Un metodo per superare questo problema consiste nell’estrarre più di una caratteristica delle forme degli impulsi (per es., la loro larghezza oltre che la loro ampiezza, e così via) e poi nel separare e classificare gli impulsi in gruppi diversi (ognuno corrispondente a un diverso neurone) sulla base della distribuzione congiunta di queste molteplici caratteristiche. La classificazione degli impulsi può essere fatta tracciando contorni che delimitano gruppi di impulsi con caratteristiche simili (per es., i gruppi di impulsi tutti con circa la stessa ampiezza o larghezza) e li dividono da altri gruppi con valori marcatamente differenti per queste caratteristiche. Strategie più complesse possono essere usate per classificare gli impulsi. Una strategia molto diffusa si basa sul memorizzare le forme degli impulsi che passano la soglia (linee nere della figura), poi individuare gruppi di forme di impulsi con caratteristiche simili e calcolare delle sagome tipiche per ogni gruppo di impulsi del neurone putativo (i gruppi di impulsi rossi e blu della figura) e poi assegnare gli impulsi al gruppo la cui sagoma è più simile alla loro.

Analisi di informazione. Il passo successivo all’identificazione e alla classificazione degli impulsi neurali è quello di usare tecniche di analisi che spieghino qual è la funzione degli impulsi emessi da ogni neurone. Un problema particolarmente importante è capire come i neuroni trasmettono informazione su stimoli sensoriali esterni (per es. il colore di immagini o la tonalità dei suoni) (➔ informazione neurale). La difficoltà principale nello studio dell’informazione neurale sta nel fatto che le risposte dei neuroni ai diversi stimoli sensoriali sono caratterizzate da una certa variabilità: la ripetuta presentazione dello stesso stimolo porta ogni volta a una risposta diversa. Questa variabilità implica che lo studio della trasmissione di informazione neurale non può essere fatto semplicemente abbinando stimoli e risposte, ma deve essere invece valutato con criteri statistici. Il più diffuso di questi criteri è basato sulla teoria dell’informazione.

Entropia e mutua informazione

Supponiamo che p(s) denoti la probabilità di presentazione dello stimolo s (che appartiene a un insieme S). Supponiamo di voler capire quale stimolo sia stato presentato solo in base alla risposta neurale r (appartenente a un insieme di possibili risposte R). Se le variabili che descrivono lo stimolo s o la risposta neurale r sono continue, supponiamo che vi sia un limite di risoluzione per la loro misura, e ordiniamo i loro valori in intervalli di dimensione pari alla risoluzione. Possiamo quindi procedere come se s e r fossero variabili a valori discreti. Prima di osservare la risposta neurale, la nostra incertezza su quale stimolo sia stato presentato è solo funzione della distribuzione p(s). Tale incertezza viene descritta dall’entropia, grandezza fondamentale nella teoria dell’informazione. Essa rappresenta una misura della variabilità di una variabile casuale, ed è definita matematicamente nel caso dello stimolo nel modo seguente: H(S)=−ΣsεS p(s)log2 p(s) Questa quantità vale zero se s non varia, cioè se p(s)=1 per un certo valore di s e p(s)=0 per tutti gli altri valori. Se ci sono K valori possibili per S, H(S) raggiunge il suo massimo valore, log2(K), quando tutti i K valori sono equiprobabili (variabilità massima), cosicché tale funzione risulta essere un’adeguata misura della variabilità. Se la risposta del neurone porta informazione sullo stimolo, allora la probabilità di osservare un certo stimolo condizionata alla osservazione di una risposta neurale ra, dovrebbe essere raggruppata intorno a un particolare valore dello stimolo sa, e i messaggi condizionati a una risposta rb intorno a un diverso valore sb. In questo caso, le distribuzioni dello stimolo p(s/ra) e p(s/rb) condizionate alle diverse risposte saranno tra loro diverse, e ognuna sarà meno uniforme della distribuzione incondizionata p(s). L’entropia condizionata media, o equivocazione, è: H(S ǀ R)=−ΣsεS ΣrεR p(r)p(s ǀ r)log2 p(s ǀ r) Questa entropia rappresenta l’incertezza residua che l’osservatore ha dopo aver osservato la risposta. La mutua informazione misura la differenza tra l’incertezza (su quale stimolo viene presentato) che un osservatore esterno del codice neurale specificato ha prima dell’osservazione della risposta neurale, e l’incertezza che l’osservatore ha dopo aver osservato la risposta. Qualsiasi misura della trasmissione di informazione si riduce così alla stima di queste entropie. La mutua informazione misura questa incertezza in unità di bit: ogni bit fornito dal neurone corrisponde a un dimezzamento dell’incertezza dell’osservatore. Volendo esprimersi con parole più semplici, un bit corrisponde all’informazione guadagnata ricevendo una risposta corretta a una domanda a cui si può rispondere solo sì o no. Un messaggio di P bit veicola un’informazione sufficiente per classificare 2P condizioni, tutte a priori equiprobabili. Uso della teoria dell’informazione per lo studio di codici neuronali

È importante notare che la quantità di mutua informazione dipende dal modo scelto per quantificare la risposta neurale r. Questo punto è molto importante ai fini pratici della ricerca: confrontando i risultati ottenuti per diverse quantificazioni della risposta neuronale, possiamo valutare quantitativamente l’efficacia di diverse ipotesi su come i neuroni codificano l’informazione. Per es., possiamo comparare l’informazione ottenuta quantificando la risposta neurale, come il numero totale di impulsi emessi dal neurone in risposta allo stimolo (codice a conteggio), con l’informazione ottenuta misurando con una precisione pari a un millisecondo l’insieme dei tempi di emissione degli impulsi neurali. Supponiamo di trovare che il codice a conteggio veicoli n bit di informazione sugli stimoli, e che l’informazione totale contenuta nella sequenza di impulsi sia di m bit. Allora ne segue che m ‒ n bit sono codificati in qualche aspetto legato alla temporizzazione degli impulsi.

Tecniche di decodifica del segnale neurale. Il problema di come le risposte neurali rappresentano gli stimoli può anche essere concettualizzato come un compito di decodifica: con quale accuratezza si può ricostruire lo stimolo, a partire dalla sequenza di impulsi evocata dallo stimolo stesso? In termini matematici, la decodifica è la predizione di quale stimolo sensoriale o comportamento ha provocato l’emissione di una certa risposta neurale osservata durante una singola presentazione dello stimolo. L’esempio più diffuso di tecniche di decodifica del segnale neurale è dato dalla cosiddetta decodifica di Bayes, in base alla quale è calcolata la predizione dello stimolo che ha provocato una certa risposta r come lo stimolo che massimizza la probabilità p(s/r) degli stimoli condizionali all’osservazione della risposta neurale r. La decodifica di Bayes ha il vantaggio che, se implementata con una stima corretta delle probabilità p(s/r), fornisce l’algoritmo di decodifica che minimizza il numero di errori nella predizione dello stimolo. I risultati della decodifica sono presentati solitamente nella forma di matrici di confusione: i valori in una riga i e colonna j di una matrice di confusione rappresentano la frazione di volte in cui la presentazione dello stimolo i è stata predetta dall’algoritmo di decodifica come stimolo j. Se il decodificatore è perfetto, la matrice di confusione ha elementi uguali a 1 lungo la diagonale e 0 fuori dalla diagonale. Se gli stimoli hanno tutti la stessa probabilità di essere presentati, una decodifica fatta in maniera casuale corrisponde a una matrice di confusione in cui tutti gli elementi sono uguali a 1/K (con K uguale al numero degli stimoli). Comparazione di vantaggi e svantaggi delle tecniche di decodifica e di calcolo di informazione. Le tecniche di analisi basate sul calcolo di informazione e di decodifica hanno vantaggi e svantaggi complementari. La teoria dell’informazione non fa ipotesi (per es., la linearità) sui meccanismi fisici attraverso i quali si codificano i messaggi; questo è al tempo stesso un vantaggio (poiché, in effetti, di questi meccanismi si sa poco) e uno svantaggio (poiché la teoria non ci dice nulla in proposito). Le tecniche di decodifica invece fanno ipotesi esplicite sugli algoritmi che devono essere usati per predire lo stimolo. Questo ha lo svantaggio di permettere conclusioni meno generali di quelle ottenute con il calcolo di informazione, ma ha il vantaggio di prestarsi a valutare la fattibilità della implementazione di specifici algoritmi di decodifica da parte di sistemi fisici con caratteristiche e limitazioni simili a quelle delle reti neurali che ricevono ed elaborano gli impulsi. Stefano Panzeri